排序算法概览
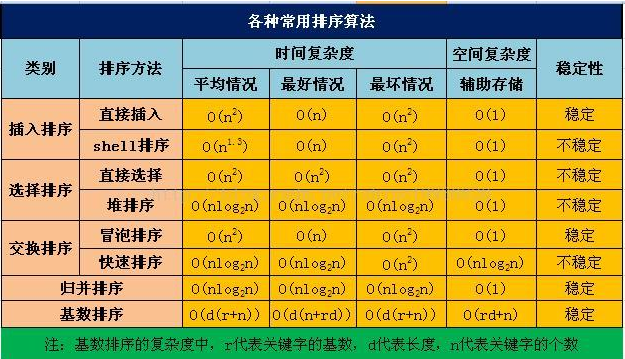
归并排序的 空间复杂度为O(n)
插入排序
基本思想是每次讲一个待排序的记录,按其关键字大小插入到前面已拍好的子序列中,直到全部完成。
直接插入排序
讲元素L(i)插入到有序序列L[1,…,i-1]中,执行以下操作:
1. 查找出L(i)在L[1,…,i-1]中的插入位置k。
2. 将L[k,…,i-1]中所有元素全部后移一位。
3. 将L(i)复制到L(k)
def InsertSort(array_a, n):
for i in range(1, n):
temp = array_a[i]
j = i - 1
while temp < array_a[j] and j >= 0:
array_a[j + 1] = array_a[j] # 如果小于其前驱,则从后往前寻找插入位置并后移。
j -= 1
array_a[j + 1] = temp
return array_a希尔排序
希尔排序的实质就是分组插入排序。
基本思想:
1. 先取一个小于n的步长d1(一般为n/2),把表分为d1个组,每个组的元素间隔个d1。
2. 在各组之内使用直接插入排序。
3. 选取第二个步长,一般为d1/2,重复上述过程,直到步长为1.
严格意义的希尔排序:
def ShellSort(array_a, n):
dk = n / 2
while dk >= 1:
for i in xrange(0, dk):
for j in range(i + dk, n, dk):
temp = array_a[j]
k = j - dk
while temp < array_a[k] and k >= 0:
array_a[k + dk] = array_a[k] # 如果小于其前驱,则从后往前寻找插入位置并后移。
k -= dk
array_a[k + dk] = temp
dk = dk / 2
return array_a其实每次元素和间隔dk倍数的前驱比较,做插入排序即可,简化版:
def ShellSort2(array_a, n):
dk = n / 2
while dk >= 1:
for i in range(dk, n):
temp = array_a[i]
k = i - dk
while temp < array_a[k] and k >= 0:
array_a[k + dk] = array_a[k] # 如果小于其前驱,则从后往前寻找插入位置并后移。
k -= dk
array_a[k + dk] = temp
dk = dk / 2
return array_a交换排序
交换即根据序列中两个元素比较结果来交换两个元素的位置。
冒泡排序
- 对于长度为n的表,从后往前依次比较两两相邻的元素值,若为逆序则交换他们的值,直到这个序列比较完,此为一趟。
- 下一趟减少一个排好元素,最终n-1趟排序完成。
def BubbleSort(array_a, n):
for i in range(0, n - 1):
flag = 0 # 交换标志
for j in range(n - 1, i, -1):
if array_a[j] < array_a[j - 1]:
temp = array_a[j]
array_a[j] = array_a[j - 1]
array_a[j - 1] = temp
flag = 1
if flag == 0:
return array_a # 若此趟未发生交换,说明已经有序,返回
return array_a快速排序
快速排序基本思想:
1. 在待排序表中任选一个元素作为pivot,以它为基准将数组分为比它大和小的两部分,此时pivot放在了最终的位置上。
2. 然后递归地对两个子表进行上述过程
3. 直到每部分都只有一个元素或者为空为止
def QuickSort(array_a, low, high):
if low < high:
pivotpos = Partition(array_a, low, high)
QuickSort(array_a, pivotpos + 1, high)
QuickSort(array_a, low, pivotpos - 1)
return array_a
def Partition(array_a, low, high):
pivot = array_a[low]
while low < high:
while low < high and array_a[high] >= pivot:
high -= 1
array_a[low] = array_a[high] # 左移比pivot小的元素
while low < high and array_a[low] <= pivot:
low += 1
array_a[high] = array_a[low] # 右移比pivot大的元素
array_a[low] = pivot
return low选择排序
基本思想:
1. 初始i=0。
2. 第i趟在后面n-i+1个元素中,选取最小的,作为第i个元素的值。
3. 一直到i=n-1做完。
简单选择排序
和上面思想一致,每趟找出最小值和第i个元素交换。找最小元素使用遍历的方法:
def SelectSort(arrau_a, n):
for i in xrange(n - 1):
min = i
for j in range(i + 1, n):
if array_a[j] < array_a[min]:
min = j
temp = array_a[i]
array_a[i] = array_a[min]
array_a[min] = temp
堆排序
堆排序是一种树形的选择排序方法,利用二叉树中双亲和孩子结点的关系,选择无序区域的关键最大(最小)的元素。
堆定义:n个关键字的序列称为堆,当且仅当其满足:
1. L(i)≤L(2i) 且L(i)≤L(2i+1)
或者
2. L(i)≥L(2i) 且L(i)≥L(2i+1)
其中1是小根堆,2是大根堆。
堆排序关键是构建初始堆,直接大根堆代码
def BuildMaxHeap(array_a, n):
for i in range(n / 2, 0, -1): # 从i=[n/2-1]~0,反复调整堆。
AdjustDown(array_a, i, n - 1)
def AdjustDown(array_a, k, n):
array_a[0] = array_a[k]
i = 2 * k
while (i <= n): # 沿着k的子结点筛选
if i < n:
if array_a[i] < array_a[i + 1]:
i += 1 # 取值更大的子结点
if array_a[0] > array_a[i]:
break
else:
array_a[k] = array_a[i] # array_a[i]调整到双亲上。
k = i
i *= 2
array_a[k] = array_a[0] # 被筛选的点放入最终位置。
def HeapSort(array_a, n):
array_a.insert(0, 0) # 首先array_a所有元素后移,rray_a[0]不存放元素
n = len(array_a)
BuildMaxHeap(array_a, n)
for i in range(n - 1, 1, -1):
temp = array_a[i]
array_a[i] = array_a[1]
array_a[1] = temp # 将最大的元素放在当前无序数组的最后
AdjustDown(array_a, 1, i - 1) # 把剩余的i-1整理成堆。归并排序
归并排序是将两个或者以上的有序表组成新的有序表。下面以二路归并为例:
递归实现:
1. 先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
2. 合并两个有序数组:
1. 数组比较a[i]和a[j]的大小。
1. 若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;
2. 否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1。
2. 如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。
def Merge(array_a, low, mid, high):
# 合并array_a的[low,...mid]和[mid+1,...high]的各自有序的两部分为一个新的有序表
b = []
for each in array_a[low:high + 1]:
b.append(each) # 将序列保存到b中。
i, j = low, mid + 1 # 其实i,j就是标记两个表比较到的位置。
k = i
while i <= mid and j <= high:
# 将较小的元素一个加入到数组array_a中。
if b[i - low] <= b[j - low]:
array_a[k] = b[i - low]
i += 1
else:
array_a[k] = b[j - low]
j += 1
k += 1
# 如果两个表有一个没有检测完,则复制。
while i <= mid:
array_a[k] = b[i - low]
k += 1
i += 1
while j <= high:
array_a[k] = b[j - low]
k += 1
j += 1
def MergeSort(array_a, low, high):
if low < high:
mid = (low + high) / 2 # 划分为两个子序列。
MergeSort(array_a, low, mid) # 分别对子序列递归排序。
MergeSort(array_a, mid + 1, high)
Merge(array_a, low, mid, high) # 合并左右两个有序的子序列。
基数排序
基数排序并不是基于比较败絮,而是采用多关键字排序思想,即基于关键字的各位大小排序,分为最高位有限和最低位优先排序。