强化学习（8）------动态规划（通俗解释）

一、动态规划

当问题具有下列两个性质时，通常可以考虑使用动态规划来求解：

1. 一个复杂问题的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解
2. 子问题在复杂问题内重复出现，使得子问题的解可以被存储起来重复利用

马尔科夫决策过程具有上述两个属性：贝尔曼方程把问题递归为求解子问题，价值函数相当于存储了一些子问题的解，可以复用。

二、MDP

马尔科夫决策过程需要解决的问题有两种：

1. 预测(Prediction)：对给定策略的评估过程。已知一个马尔科夫决策过程以及策略，目标是求解基于该策略的价值函数  ，即处于每个状态下能够获得的奖励(reward)是多少。
2. 控制(Control)：寻找一个最优策略的过程。已知一个马尔科夫决策过程但是策略未知，求解最优价值函数  和最优策略  。

动态规划算法的核心是用值函数来构建对最优策略  的搜索，如果最优值函数  和  已知，就能获得最优策略  。其中  和  满足如下方程：

 

三、策略评估(Policy Evaluation)

策略评估 (Policy Evaluation) 指计算给定策略下状态价值函数  的过程。

策略评估可以使用同步迭代联合动态规划的算法：从任意一个状态价值函数开始，依据给定的策略，结合贝尔曼期望方程、状态转移概率和奖励，同步迭代更新状态价值函数直至其收敛，得到该策略下最终的状态价值函数。理解该算法的关键在于在一个迭代周期内如何更新每一个状态的价值。 

策略评估的例子

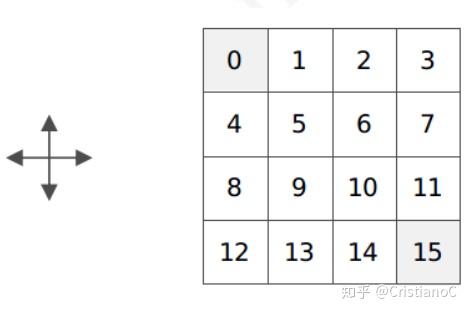
状态空间s：上面4×4为一个小世界，该世界有16个状态，每个小方格对应一个状态（0-15），其中，0和15是终止状态。

行为空间A：可上下左右移动，移动到0或15任意一个即完成任务。

转移概率P：

四、策略提升 (Policy Improvement)

五、策略迭代 (Policy Iteration)

策略迭代一般分成两步：

• 策略评估(Policy Evaluation)：基于当前的策略计算出每个状态的价值函数
• 策略提升 (Policy Improvement)：基于当前的价值函数，采用贪心算法来找到当前最优的策略

、

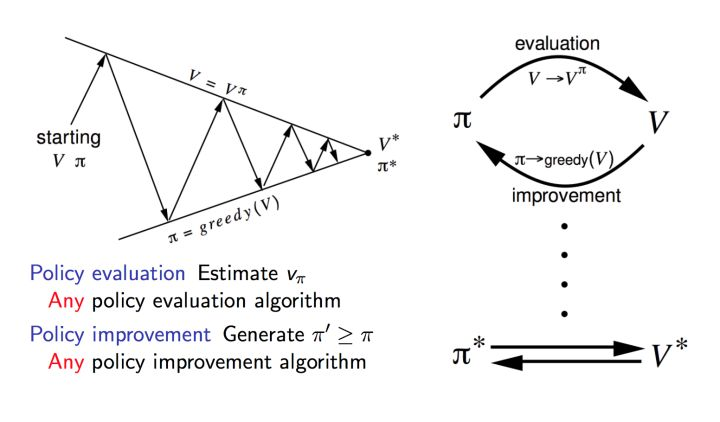本质上就是使用当前策略产生新的样本，然后使用新的样本更好的估计策略的价值，然后利用策略的价值更新策略，然后不断反复。由于一个有限的马尔可夫决策过程只有有限个策略，这个过程一定能够在有限的迭代次数后收敛到最优的策略和最优的价值函数。

六、值迭代 (Value Iteration)

参考：

https://zhuanlan.zhihu.com/p/72360992