相机与图像
1. 理解针孔相机的模型、内参与径向畸变参数。
总结在前: 单目相机的成像过程:
1. 首先,世界坐标系下有一个固定的点 P,世界坐标为 Pw;
2. 由于相机在运动,它的运动由 R; t 或变换矩阵 T 2 SE(3) 描述。 P 的相机坐标为: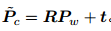
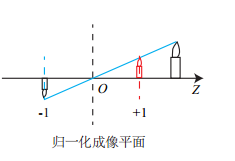
3. 这时的 P~c 仍有 X; Y; Z 三个量,把它们投影到归一化平面 Z = 1 上,得到 P 的归一化相机坐标: Pc = [X/Z; Y /Z; 1]T ‹。
4. 最后, P 的归一化坐标经过内参后,对应到它的像素坐标: 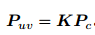
使用针孔和畸变两个模型来描述整个投影过程,这两个模型能够把外部的三维点投影到相机内部成像平面,构成了相机的内参数
针孔模型: 描述了一束光线通过针孔之后,在针孔背面投影成像的关系
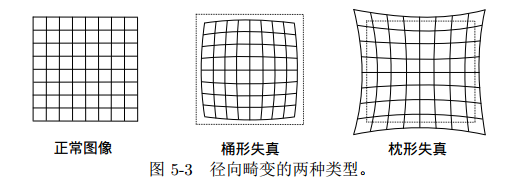
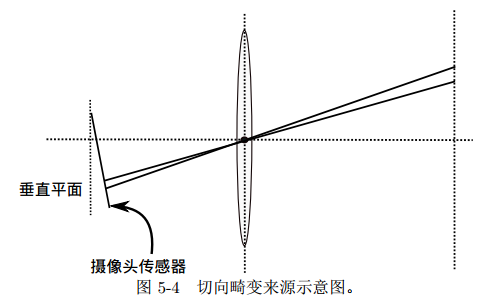
由于透镜的存在,会使得光线投影到成像平面的过程中会产生畸变
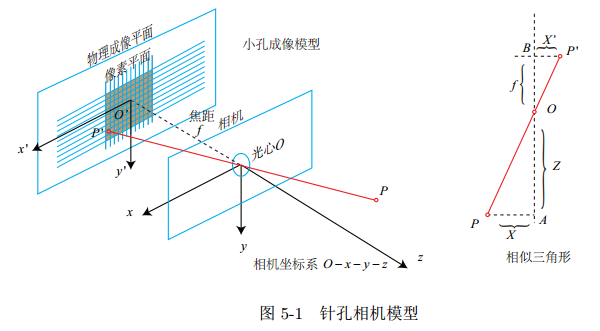
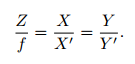
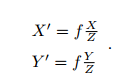
像素坐标系:
像素坐标系‹通常的定义方式是:原点 o′ 位于图像的左上角, u 轴向右与 x 轴平行, v轴向下与 y 轴平行。像素坐标系
与成像平面之间,相差了一个缩放和一个原点的平移。
设像素坐标在 u 轴上缩放了 α 倍,在 v 上缩放了 β 倍。同时,原点平移了 [cx; cy]T。那
么, P ′ 的坐标与像素坐标 [u; v]T 的关系为:
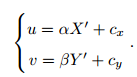 代入上一个公式,
代入上一个公式,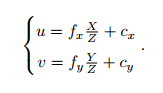 αf 合并成 fx,把 βf 合并成 fy
αf 合并成 fx,把 βf 合并成 fy
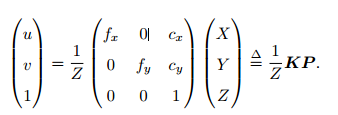
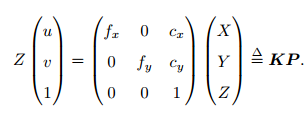 中间的矩阵就是相机的内参矩阵K。确定相机内参就是标定
中间的矩阵就是相机的内参矩阵K。确定相机内参就是标定
外参
相机的位姿 R; t 又称为相机的外参数
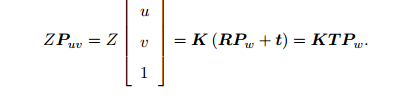 去掉z
去掉z

右侧的 T Pw 表示把一个世界坐标系下的齐次坐标,变换到相机坐标系下。
为了使它与 K 相乘,需要取它的前三维组成向量——因为 T Pw 最后一维为 1。
把最后一维进行归一化处理,得到了 P 在相机归一化平面上的投影 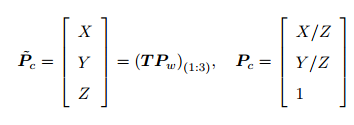 Pc 经过内参之后就得到了像素坐标
Pc 经过内参之后就得到了像素坐标
畸变
双目相机模型:
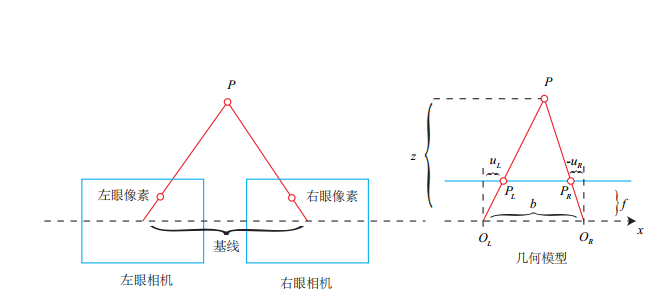

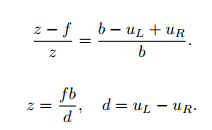
d为视差。视差与距离成反比:视差越大,距离越近
RGB-D模型
1.通过红外结构光(Structured Light)来测量像素距离的。例子有 Kinect 1 代、 Project
Tango 1 代、 Intel RealSense
2. 通过飞行时间法(Time-of-flight, ToF)原理测量像素距离的。例子有 Kinect 2 代和
一些现有的 ToF 传感器
2. 理解一个空间点是如何投影到相机成像平面的。
3. 掌握 OpenCV 的图像存储与表达方式。
4. 学会基本的摄像头标定方法。
实践:
1.操作opencv图像