背包问题的动态规划算法
01背包问题我最初学会的解法是回溯法,第一反应并不是用动态规划算法去解答。原因是学习动态规划算法的时候,矩阵连乘、最长公共子串等问题很容易将问题离散化成规模不同的子问题,比较好理解,而对于01背包问题则不容易想到将背包容量离散化抽象出子问题,从情感上先入为主也误以为动态规划算法不是解决01背包问题的好方法,实际上并不是这样的。
问题描述:给定n种物品和一背包,物品i的重量是wi,其价值为vi,背包的容量为C,求能装入背包的物品的最大价值。
用m(i,j)表示为从i到n的序列装入容量为j的背包能产生的最大价值,则能装入背包的物品最大价值为m(1,C)。
递归式为:
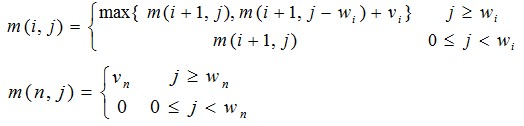
上面讲到,该问题是对背包的容量进行离散化,因此时间复杂度是O(nC)。
代码如下(用的变量名可能和上面有小出入,但是是自描述的):
#include<iostream> using namespace std; struct CARGO{ int weight; int value; }; const int totalWeight=10; const int totalNumber=5; CARGO goods[totalNumber]={{2,6},{2,3},{6,5},{5,4},{4,6}}; //1.下标都从1开始;2.遇到复杂结构的初始化用memset方法。 int result[totalNumber+1][totalWeight+1]={0}; int myMax(int i,int j) { return i>=j?i:j; } void dp() { int i,j; //动态规划表达式的初始化 i=totalNumber; for(j=1;j<=totalWeight;j++) { if(goods[i-1].weight>j)//为保证逻辑完整性,这个if没删掉 { result[i][j]=0; } else { result[i][j]=goods[i-1].value; } } for(i=totalNumber-1;i>0;i--) { for(j=1;j<=totalWeight;j++) { if(goods[i-1].weight>j) { result[i][j]=result[i+1][j]; } else { result[i][j]=myMax(result[i+1][j],result[i+1][j-goods[i-1].weight]+goods[i-1].value); } } } } int main() { dp(); cout<<result[1][totalWeight]<<endl; //是否理解:完成用result[totalNumber][totalWeight]表示背包最大value的代码(从前往后解决子问题的方法)。 return 0; }
