我们知道max,假如说我有两个数,a和b,并且a>b,如果取max,那么就直接取a,没有第二种可能。但有的时候我不想这样,因为这样会造成分值小的那个饥饿。所以我希望分值大的那一项经常取到,分值小的那一项也偶尔可以取到,那么我用softmax就可以了 现在还是a和b,a>b,如果我们取按照softmax来计算取a和b的概率,那a的softmax值大于b的,所以a会经常取到,而b也会偶尔取到,概率跟它们本来的大小有关。所以说不是max,而是 Soft max 那各自的概率究竟是多少呢,我们下面就来具体看一下
定义
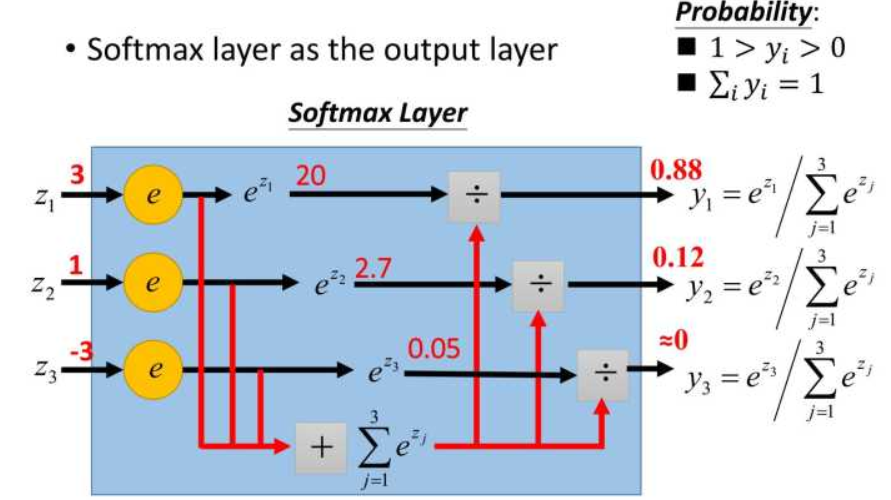
假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个元素的Softmax值就是
也就是说,是该元素的指数,与所有元素指数和的比值
这个定义可以说非常的直观,当然除了直观朴素好理解以外,它还有更多的优点
《一天搞懂深度学习》:
1.计算与标注样本的差距
在神经网络的计算当中,我们经常需要计算按照神经网络的正向传播计算的分数S1,和按照正确标注计算的分数S2,之间的差距,计算Loss,才能应用反向传播。Loss定义为交叉熵
取log里面的值就是这组数据正确分类的Softmax值,它占的比重越大,这个样本的Loss也就越小,这种定义符合我们的要求
2.计算上非常非常的方便
当我们对分类的Loss进行改进的时候,我们要通过梯度下降,每次优化一个step大小的梯度
我们定义选到yi的概率是
然后我们求Loss对每个权重矩阵的偏导,应用链式法则
最后结果的形式非常的简单,只要将算出来的概率的向量对应的真正结果的那一维减1,就可以了
举个例子,通过若干层的计算,最后得到的某个训练样本的向量的分数是[ 1, 5, 3 ], 那么概率分别就是[0.015,0.866,0.117],如果这个样本正确的分类是第二个的话,那么计算出来的偏导就是[0.015,0.866−1,0.117]=[0.015,−0.134,0.117]然后再根据这个进行back propagation就可以了