Multi String Search

refer to: https://www.algoexpert.io/questions/Multi%20String%20Search

---

Input: a big string and an array of small strings, the length of every string in the array is smaller than the length of the big string

Output: a boolean string, which every index represents the particular small string is contained in the big string or not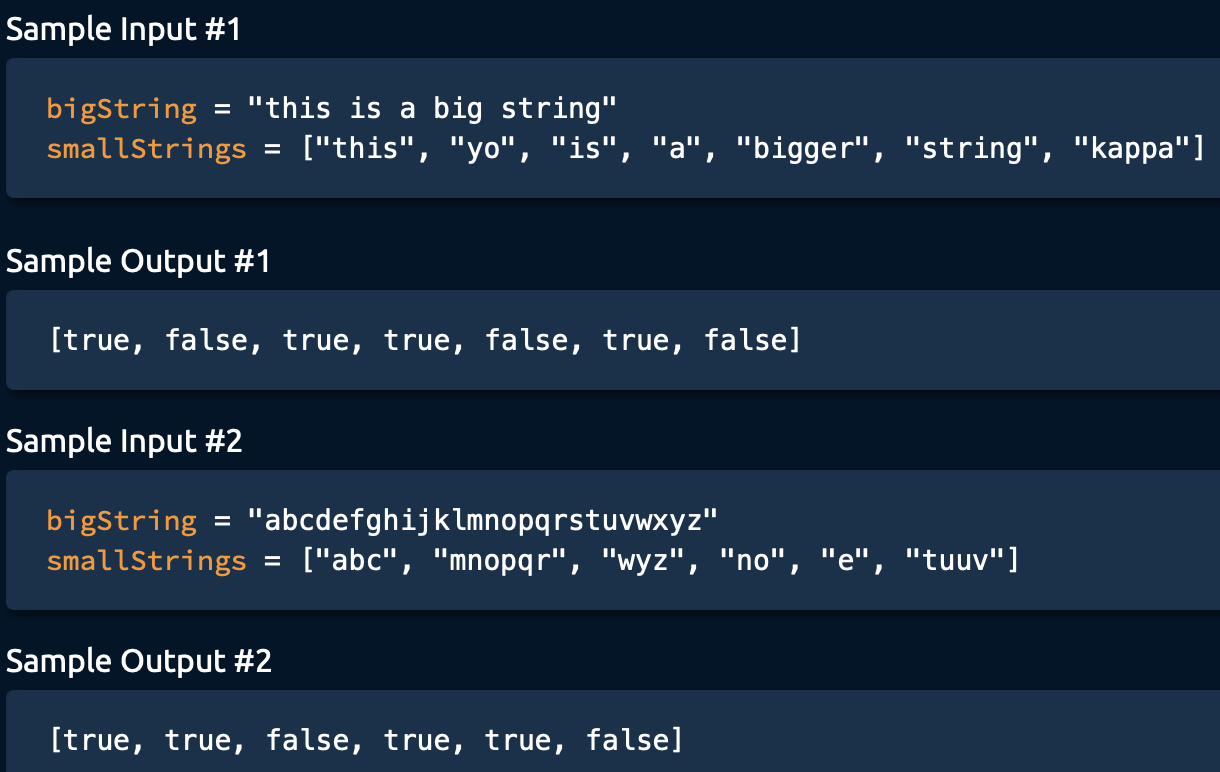

Analysis

Approach 1

naive approach, iterate through all of the small strings, for every small string, traverse the whole big string, time complexity: O(mnl), where m is the length of the array of small strings, n is the length of the big string, and l is the biggest length of small string. Space complexity is O(m) -> the size of the output array.

code

def multiStringSearch(bigString, smallStrings):
    return [isInBigString(bigString, smallString) for smallString in smallStrings]

def isInBigString(bigString, smallString):
    for i in range(len(bigString)):
        if i + len(smallString) > len(bigString):
            break
        if isInBigStringHelper(bigString, smallString, i):
            return True
    return False

def isInBigStringHelper(bigString, smallString, startIdx):
    # compare the two strings from startIdx
    leftBigIdx = startIdx
    rightBigIdx = startIdx + len(smallString) - 1
    leftSmallIdx = 0
    rightSmallIdx = len(smallString) - 1
    while leftBigIdx <= rightBigIdx:
        if bigString[leftBigIdx] != smallString[leftSmallIdx] or bigString[rightBigIdx] != smallString[rightSmallIdx]:
            return False
        leftBigIdx += 1
        rightBigIdx -= 1
        leftSmallIdx += 1
        rightSmallIdx -= 1
    return True

Approach 2

build a suffix-trie containing all of the big string's suffixes. 后缀树，to build this suffix trie like data structrue, it takes O(n^2) time and O(n^2) space, where n is the length of the big string.

To check if a sring is contained in a suffixex trie, it takes O(len(string)) time. In this case, it takes O(biggest length of small string) for check if a string is contained in the big string. To finish checking the whole array of small strings, we will take O(ml) time to check the whole array of strings, where m is the length of the array, l is the biggest length of small string. In total, we will take O(n^2 + ml) time, where O(n^2) is the suffix trie construction and O(ml) is the checking step. Space complexity is O(n^2 + m). O(n^2) is the space for suffix trie, O(m) is to store the output array.

Code

def multiStringSearch(bigString, smallStrings):
    modifiedSuffixTrie = ModifiedSuffixTrie(bigString)# construct the suffix trie
    return [modifiedSuffixTrie.contains(string) for string in smallStrings] # check every string is in the suffix trie

class ModifiedSuffixTrie:
    def __init__(self, string):
        self.root = {}
        self.populateModifiedSuffixTrieFrom(string)   # add string into the suffix trie
    
    def populateModifiedSuffixTrieFrom(self, string): # for each string, add each suffix trie, start indices included.
        for i in range(len(string)): 
            self.insertSubstringStartingAt(i, string)
            
    def insertSubstringStartingAt(self, i, string):   # given a start index, insert the substring in the suffix trie
        node = self.root
        for j in range(i, len(string)): # iterate erevy letter from index i 
            letter = string[j]  # the current letter
            if letter not in node:
                node[letter] = {} # create an empty hashmap to build a new root tree
            node = node[letter] # update the node, traverse down the tree
    
    def contains(self, string): # check a string is contained in the suffix tries
        node = self.root
        for letter in string:
            if letter not in node:
                return False
            node = node[letter] # update the node, traverse down the tree

   return True

Approach 3

build a suffix trie based on array of small strings. suffix trie construction: O(ml) time, where m is the length of the array, l is the biggest length of small string; O(ml) space to store the suffix tries. 

Search: O(nl), where n is the length of the big string, l is the longest small string in the array.

In total: time complexity: O(ml + nl).  space complexity: O(ml + m)->O(ml)

code

def multiStringSearch(bigString, smallStrings):
    trie = Trie()
    for string in smallStrings:
        trie.insert(string)
    containedStrings = {}
    for i in range(len(bigString)):
        findSmallStringsIn(bigString, i, trie, containedStrings)
    return [string in containedStrings for string in smallStrings]

def findSmallStringsIn(string, startIdx, trie, containedStrings):
    currentNode = trie.root
    for i in range(startIdx, len(string)):
        currentChar = string[i]
        if currentChar not in currentNode:
            break
        currentNode = currentNode[currentChar]
        if trie.endSymbol in currentNode:
            containedStrings[currentNode[trie.endSymbol]] = True

class Trie:
    def __init__(self):
        self.root = {}
        self.endSymbol = "*"
        
    def insert(self, string):
        current = self.root
        for i in range(len(string)):
            if string[i] not in current:
                current[string[i]] = {}
            current = current[string[i]]
        current[self.endSymbol] = string

Comparing

appoach 1: O(mnl)

appoach 2: O(n^2 + ml)

appoach 3: O(nl + ml)

compare l and n, where n is the length of the big string, l is the longest length of small strings

In the problem description, we know that the length of every string in the array is smaller than the length of the big string, so appoach 3 is better than approach 2.