上承:卡特兰数知识讲解
在学完了卡特兰数的知识之后,我们来看几道例题,研究一下卡特兰数的运用。
题意:用 $n$ 个 $1$ 和 $m$ 个 $0$ 拼成的任意前缀都满足 $1$ 的个数不小于 $0$ 的个数的字符串的个数对质数 $20100403$ 取模的结果。 $(1le mle nle10^6)$
题解:我们发现前缀限制与卡特兰数的 $y=x$ 限制很像,于是就考虑将字符串转换为二维平面上的路径,让 $1$ 表示向右走一步, $0$ 表示向上走一步,则前缀个数限制变为不穿过 $y=x$ 这一直线。现在我们要求从 $(0,0)$ 到 $(n,m)$ 的路径条数。我们继续沿用卡特兰的翻转思想,求总路径数-穿过 $y=x$ 的路径数,将穿过直线的路径从其第一个穿过的位置开始翻转,于是终点变为 $(m-1,n+1)$ ,并且穿过直线的路径与翻转后从 $(0,0)$ 到终点的路径一一对应,于是答案就是 $ binom{n+m}{n}- binom{n+m}{m-1}$ ,预处理阶乘与其逆元快速计算即可。
启发:该题的模型转换与计数时的思想类比还是很巧妙的,值得学习。
题意:求用 $n$ 个任意大小的矩形拼成一个高度为 $n$ 的阶梯的方案数。(下图为 $n=3$ 的情况)。(不取模, $1le nle 500$ )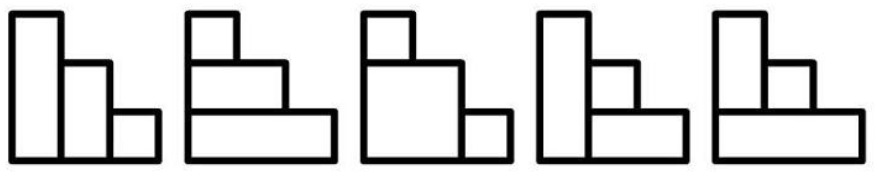
我们考虑以包含左下角的矩形为切入点,它一定会顶到阶梯的右上角(否则覆盖每个右上角的点都需要一个矩形,总个数大于 $n$ ),因此它将阶梯分为两个小阶梯,于是我们在意料之中惊奇地发现它是个卡特兰数并解决了这道题。
启发:选好切入点,将原问题分为两半,这一卡特兰数的思想对我们大有帮助。
好了,你已经掌握了卡特兰数的基本内容,来做一下这道习题吧!