听上去有丶厉害,实际也很巧妙
学习了这两篇:ReMoon - 单调栈的应用 --- 笛卡尔树与虚树
ACM算法日常 - 算法合集 | 神奇的笛卡尔树 - HDU 1506
板子:

struct Cartesian { int root; int ls[N],rs[N]; vector<int> v; void clear() { root=0; v.clear(); for(int i=1;i<n;i++) ls[i]=rs[i]=0; } void build(int *a) { for(int i=1;i<n;i++) { int j=0; //a[v.back()]<a[i] 大根 //a[v.back()]>a[i] 小根 while(v.size() && a[v.back()]<a[i]) j=v.back(),v.pop_back(); if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } };
~ 简介 ~
虽然名字中带有“树”,但是笛卡尔树其实是对于一个序列的转化,并通过这个转化获得更多此序列的信息
对于一个简单的序列:$2,8,5,7,1,4$,我们可以建立如下的笛卡尔树($pos$表示原序列中的位置,$val$表示该位置的值)
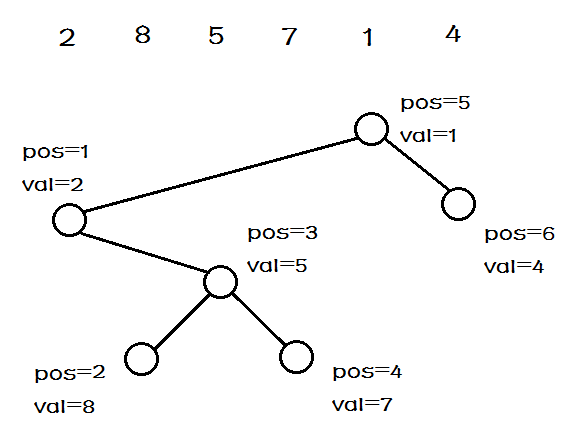
笛卡尔树有这样的基本性质:
对于树上的任意一点$x$和左右儿子$left,right$,有:
1. $pos[left]<pos[x]<pos[right]$
2. $val[x]<val[left],val[right]$
即一般讲解所说的$pos$满足二叉查找树,$val$满足堆
直观点说,就是这两条延伸性质:
以树上任意一点$x$为根构成的子树中,
1. 各节点的$pos$是连续的,且对$pos$的中序遍历即为原序列顺序(由$pos$满足二叉查找树可得)
2. $x$点的$val$为全子树最小(由$val$满足堆可得)
~ 建树 ~
有了对笛卡尔树结构的了解,现在考虑怎么建立这棵树
【方法一】优先满足$val$
要想优先满足$val$的条件,那就必须从顶向下建树了
利用上面的延伸性质2,每次选取当前区间$[l,r]$中$val$的最小值所在的$pos$(记$pos=i$)作为子树的根节点
然后对于$[l,i-1],[i+1,r]$递归地不断重复上述过程
其中选取区间$val$最小值所在的$pos$可以使用线段树优化
总复杂度$O(nlogn)$

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; const int INF=1<<30; int n; int val[N]; int sz; int t[N<<2]; inline void Add(int i) { int k=i+sz-1; t[k]=i; k>>=1; while(k) { int left=t[k<<1],right=t[k<<1|1]; t[k]=(val[left]<val[right]?left:right); k>>=1; } } inline int Query(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0; if(a>=l && b<=r) return t[k]; int mid=(a+b)>>1; int left=Query(k<<1,l,r,a,mid),right=Query(k<<1|1,l,r,mid+1,b); return (val[left]<val[right]?left:right); } void Init() { sz=1; while(sz<n) sz<<=1; val[0]=INF; for(int i=1;i<(sz<<1);i++) t[i]=0; for(int i=1;i<=n;i++) Add(i); } int ls[N],rs[N]; inline int Build(int l,int r) { if(l>r) return 0; int pos=Query(1,l,r,1,sz); ls[pos]=Build(l,pos-1); rs[pos]=Build(pos+1,r); return pos; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&val[i]); Init(); int root=Build(1,n); /* for(int i=1;i<=n;i++) printf("i=%d: ls=%d rs=%d ",i,ls[i],rs[i]);*/ return 0; }
【方法二】优先满足$pos$
由于对于子树的先序遍历是原序列顺序,所以考虑按$i=1 ext{ ~ }n$的顺序依次加入节点并调整树的结构,使得当前的树为子序列$[1,i]$所构成的笛卡尔树
由于$pos$满足二叉排序树,而$i$在区间$[1,i]$中$pos$最大,所以$i$插入的位置为 序列$[1,i-1]$所构成的笛卡尔树的根节点 一直向右儿子走、直到走到了空节点
这样插入后,$i$的$pos$已经满足要求了,但是$val$却不一定满足堆
于是考虑怎么调整当前的树
若$i$的$val$不满足要求,即存在某(些)祖先$j$,使得$j$为根的子树中$val$全大于$val[i]$;显然我们需要通过调整$i$的位置,使得$i$成为$j$的祖先
是这样操作的:
0. 刚刚插入完成后,可能树是这样的
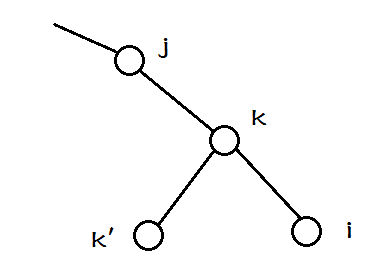
1. 将$i$向上一层移动;这时由于$pos[k]<pos[i]$,所以$k$成为$i$的左儿子,$k'$依然是$k$的左儿子

2. 继续将$i$向上一层移动,相似的,$j$也应当属于$i$的左子树;不妨让$j$为$i$的左儿子,$k$为$j$的右儿子(使用这种调整方法,$j,k,k'$相互间与原来的连边相同)

以上的调整操作都是在$[1,i-1]$序列构成的笛卡尔树的最右链(即从根节点一直向右儿子走的这条路径)上进行的
在处理完后,我们对比一下调整前后的树结构,发现只有很少的地方出现了变化:
1. $k$的右儿子变成了空节点
2. $j$的父亲变成了$i$,且$j$是$i$的左儿子
3. $i$继承了原来$j$的父亲
事实上,即使$i$到$j$的路径很长很长,一共也只有这三个地方发生了变化,所以我们的调整不是很复杂
现在最大的问题变成,如何找到$j$
目光回到最右链上,由于$val$满足堆,于是最右链上的各节点$val$是单调递增的;可以考虑用单调栈维护,栈中装的是最右链上节点的$pos$
而我们要找的$j$,就是$val[j]<val[i]$、且最靠近栈底的元素
原理理解了之后,重新整理一下思路,尽量简单清楚地建笛卡尔树:
1. 用单调栈维护最右链
2. 每次插入当前的$i$,在单调栈中不停弹出栈顶,直到栈顶$fa$满足$val[fa]<val[i]$,则最后一次弹出的就是$j$
3. 将$i$作为$fa$的右儿子,$j$作为$i$的左儿子
是不是很简单owo
复杂度$O(n)$,是相当优秀的一种方法

#include <cstdio> #include <cstring> #include <algorithm> #include <vector> using namespace std; const int N=100005; int n; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]>a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); Build(); /* for(int i=1;i<=n;i++) printf("i=%d ls=%d rs=%d ",i,ls[i],rs[i]);*/ return 0; }
所以在一些情况下,笛卡尔树的题目可以不用建树,直接用单调栈就够了
~应用~
最简单的一个应用是求元素的左右延伸区间
具体点说,就是对于一个数列$a$,询问以$a[i]$为区间最大(小)值的最长区间
使用笛卡尔树,就可以通过$O(n)$的预处理做到$O(1)$查询:进行中序遍历,每个节点$x$的子树的$pos$最小、最大值就是答案
模板题:HDU 1506 ($Largest Rectangle in a Histogram$)

#include <cstdio> #include <cstring> #include <algorithm> #include <vector> using namespace std; typedef long long ll; const int N=100005; int n; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { v.clear(); memset(ls,0,sizeof(ls)); memset(rs,0,sizeof(rs)); for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]>a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; void dfs(int x) { l[x]=r[x]=x; if(ls[x]) { dfs(ls[x]); l[x]=l[ls[x]]; } if(rs[x]) { dfs(rs[x]); r[x]=r[rs[x]]; } } int main() { scanf("%d",&n); while(n) { for(int i=1;i<=n;i++) scanf("%d",&a[i]); Build(); dfs(root); ll ans=0; for(int i=1;i<=n;i++) ans=max(ans,ll(a[i])*(r[i]-l[i]+1)); printf("%lld ",ans); scanf("%d",&n); } return 0; }
一个稍微高级一点的应用,就是给出分治的边界
一道不错的题:Luogu P4755 ($Beautiful Pair$)
官方题解已经很完善了:FlierKing - 题解 P4755 【Beautiful Pair】
简单点说,就是每次取当前区间$[l,r]$的最大值$a_i$,那么$i$即为笛卡尔树中 此区间对应子树的根节点
于是将区间分成两部分$[l,i-1],[i+1,r]$的操作,就可以转化成笛卡尔树上的分治
同时,这个题解将“统计$[l,r]$中$a_ileq x$的数量”这个主席树问题,离线后通过拆分转化为树状数组问题,设计十分巧妙

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=100005; int n; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]<a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; inline void dfs(int x) { if(ls[x]) { dfs(ls[x]); l[x]=l[ls[x]]; } else l[x]=x; if(rs[x]) { dfs(rs[x]); r[x]=r[rs[x]]; } else r[x]=x; } vector<pii> add[N]; inline void Solve(int x) { int lp=x-l[x],rp=r[x]-x; if(lp<rp) for(int i=l[x];i<=x;i++) { add[r[x]].push_back(pii(a[x]/a[i],1)); add[x-1].push_back(pii(a[x]/a[i],-1)); } else for(int i=x;i<=r[x];i++) { add[x].push_back(pii(a[x]/a[i],1)); add[l[x]-1].push_back(pii(a[x]/a[i],-1)); } if(ls[x]) Solve(ls[x]); if(rs[x]) Solve(rs[x]); } vector<int> pos; int t[N]; inline int lowbit(int x) { return x&(-x); } inline void Add(int k,int x) { for(int i=k;i<=n;i+=lowbit(i)) t[i]+=x; } inline int Query(int k) { int res=0; for(int i=k;i;i-=lowbit(i)) res+=t[i]; return res; } int main() { scanf("%d",&n); pos.push_back(0); for(int i=1;i<=n;i++) scanf("%d",&a[i]),pos.push_back(a[i]); sort(pos.begin(),pos.end()); pos.resize(unique(pos.begin(),pos.end())-pos.begin()); Build(); dfs(root); Solve(root); ll ans=0; for(int i=1;i<=n;i++) { int p=lower_bound(pos.begin(),pos.end(),a[i])-pos.begin(); Add(p,1); for(int j=0;j<add[i].size();j++) { int lim=lower_bound(pos.begin(),pos.end(),add[i][j].first)-pos.begin(); if(pos[lim]>add[i][j].first) lim--; ans=ans+add[i][j].second*Query(lim); } } printf("%lld ",ans); return 0; }
学完之后立马就现场碰到基本一样的题...
牛客ACM 883G ($Removing Stones$,2019牛客暑期多校训练营(第三场))
只不过对于当前区间,是遍历较小的那一半、并在另一半二分

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=300005; int n; int a[N]; ll p[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]<a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; inline void dfs(int x) { if(ls[x]) { dfs(ls[x]); l[x]=l[ls[x]]; } else l[x]=x; if(rs[x]) { dfs(rs[x]); r[x]=r[rs[x]]; } else r[x]=x; } ll ans=0; void Solve(int x) { ll sum=0; int lp=x-l[x]+1,rp=r[x]-x+1; int left,right,mid; if(lp<rp) for(int i=x;i>=l[x];i--) { sum+=a[i]; left=x,right=r[x]+1,mid; while(left<right) { mid=(left+right)>>1; if(sum+p[mid]-p[x]<2LL*a[x]) left=mid+1; else right=mid; } ans+=r[x]-left+1; } else for(int i=x;i<=r[x];i++) { sum+=a[i]; left=l[x],right=x,mid; while(left<right) { mid=(left+right)>>1; if(sum+p[x-1]-p[mid-1]>=2LL*a[x]) left=mid+1; else right=mid; } if(sum+p[x-1]-p[left-1]<2LL*a[x]) left--; ans+=left-l[x]+1; } if(ls[x]) Solve(ls[x]); if(rs[x]) Solve(rs[x]); } void Clear() { ans=0; v.clear(); for(int i=1;i<=n;i++) ls[i]=rs[i]=0; } int main() { int T; scanf("%d",&T); while(T--) { Clear(); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),p[i]=p[i-1]+a[i]; Build(); dfs(root); Solve(root); printf("%lld ",ans); } return 0; }
一道比较明显的题:HDU 6701 ($Make Rounddog Happy$,$2019 Multi-University Training Contest 10$)
由于需要对$a_l,...,a_r$求max,所以能比较自然地想到笛卡尔树上分治
然后就是处理区间内数字不同的限制;不过也并不困难,只要正向、反向各扫一遍就能预处理出来$i$向左、向右不出现重复数字的最大延伸长度了

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=300005; int n,k; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { v.clear(); for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]<a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; void dfs(int x) { l[x]=r[x]=x; if(ls[x]) dfs(ls[x]),l[x]=l[ls[x]]; if(rs[x]) dfs(rs[x]),r[x]=r[rs[x]]; } int cnt[N]; int L[N],R[N]; ll ans=0; void Solve(int x) { int lp=x-l[x],rp=r[x]-x; if(lp<rp) { for(int i=l[x];i<=x;i++) ans+=max(0,min(R[i],r[x])-max(a[x]-k+i-1,x)+1); } else { for(int i=x;i<=r[x];i++) ans+=max(0,min(k-a[x]+i+1,x)-max(L[i],l[x])+1); } if(ls[x]) Solve(ls[x]); if(rs[x]) Solve(rs[x]); } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&k); ans=0; for(int i=1;i<=n;i++) ls[i]=rs[i]=0; for(int i=1;i<=n;i++) scanf("%d",&a[i]); Build(); dfs(root); int j=1; for(int i=1;i<=n;i++) { cnt[a[i]]++; while(cnt[a[i]]>1) { R[j]=i-1; cnt[a[j]]--; j++; } } for(int i=j;i<=n;i++) R[i]=n,cnt[a[i]]--; j=n; for(int i=n;i>=1;i--) { cnt[a[i]]++; while(cnt[a[i]]>1) { L[j]=i+1; cnt[a[j]]--; j--; } } for(int i=j;i>=1;i--) L[i]=1,cnt[a[i]]--; Solve(root); printf("%lld ",ans); } return 0; }
标算是左偏树,不过用笛卡尔树+倍增也能搞过去:HDU 5575 ($Discover Water Tank$,$2015 ACM/ICPC$上海)
首先可以根据隔板的高度,对于$n-1$个隔板建立一个大根笛卡尔树
有了这棵笛卡尔树,我们可以考虑利用它来划分出分治区间
比如,对于笛卡尔树根节点对应原序列的位置$pos_{root}$,相当于将$1 ext{~}n$的区间划分成两部分$[1,pos_{root}],[pos_{root}+1,n]$,且每部分的水位最高都不超过$h[pos_{root}]$;其余节点的划分同理
我们先将每个查询分配到划分树上,具体方法是,先倍增出每个划分树节点的父亲关系,然后对于每个查询${x,y,w}$,从$[x,x]$对应的区间,向上找到树上最深的 水位限制大于等于$y$的祖先,并将这个查询扔到那个节点的vector中
于是考虑树形dp
对于一个区间,要不将它整体灌满,要不不灌满、并向下递归;所以对于每个划分树上的节点,分别记录灌满和不灌满的 最多正确询问数
注意$y$的边界即可(我的处理是将每个$y++$)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct Query { int x,y,w; Query(int a,int b,int c) { x=a,y=b,w=c; } }; inline bool operator <(Query A,Query B) { return A.y<B.y; } inline bool operator >(Query A,Query B) { return A.y>B.y; } const int INF=1<<30; const int N=200005; const int LOG=20; int n,m; int h[N]; struct Cartesian { int root; int ls[N],rs[N]; vector<int> v; void clear() { root=0; v.clear(); for(int i=1;i<n;i++) ls[i]=rs[i]=0; } void build() { for(int i=1;i<n;i++) { int j=0; while(v.size() && h[v.back()]<h[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } }tree; int tot; int lb[N],rb[N],lim[N]; int ls[N],rs[N]; int fa[N][LOG]; int place[N]; void Build(int x,int y,int l,int r,int f) { lb[x]=l,rb[x]=r; fa[x][0]=f; if(l==r) { place[l]=x; return; } ls[x]=++tot; lim[tot]=h[y]; Build(tot,tree.ls[y],l,y,x); rs[x]=++tot; lim[tot]=h[y]; Build(tot,tree.rs[y],y+1,r,x); } int sum[N],sub[N]; vector<Query> v[N]; void dfs(int x) { if(ls[x]) dfs(ls[x]); if(rs[x]) dfs(rs[x]); int empty=0,full=0; for(int i=0;i<v[x].size();i++) { Query tmp=v[x][i]; if(tmp.w==0) empty++; } sub[x]=sub[ls[x]]+sub[rs[x]]+empty; for(int i=0;i<v[x].size();) { int j=i; while(j<v[x].size() && v[x][i].y==v[x][j].y) { Query tmp=v[x][j]; if(tmp.w==0) empty--; if(tmp.w==1) full++; j++; } i=j; sub[x]=max(sub[x],sum[ls[x]]+sum[rs[x]]+full+empty); } sum[x]=sum[ls[x]]+sum[rs[x]]+full; } int main() { int T; scanf("%d",&T); for(int kase=1;kase<=T;kase++) { scanf("%d%d",&n,&m); for(int i=1;i<n;i++) scanf("%d",&h[i]); tree.clear(); tree.build(); for(int i=1;i<=tot;i++) { v[i].clear(); ls[i]=rs[i]=fa[i][0]=0; sum[i]=sub[i]=0; } tot=1; lim[1]=INF; Build(1,tree.root,1,n,0); for(int i=1;i<LOG;i++) for(int j=1;j<=tot;j++) fa[j][i]=fa[fa[j][i-1]][i-1]; for(int i=1;i<=m;i++) { int x,y,w; scanf("%d%d%d",&x,&y,&w); Query tmp(x,++y,w); int p=place[x]; for(int j=LOG-1;j>=0;j--) if(fa[p][j] && y>lim[fa[p][j]]) p=fa[p][j]; if(y>lim[p]) p=fa[p][0]; v[p].push_back(tmp); } for(int i=1;i<=tot;i++) sort(v[i].begin(),v[i].end()); dfs(1); printf("Case #%d: %d",kase,sub[1]); putchar(' '); } return 0; }
一般都是银牌题难度的样子吧,平常见的不多,遇到再补充
Nowcoder 209390 (Sort the String Revision,2020牛客暑期多校第四场)
(完)
