斜率优化DP

先摆上学习的文章：

orzzz：斜率优化dp学习

Accept：斜率优化DP

感谢dalao们的讲解，还是十分清晰的

---

斜率优化$DP$的本质是，通过转移的一些性质，避免枚举地得到最优转移

经典题：HDU 3507 （$Print$ $Article$）

状态数$O(N)$，单次转移$O(N)$的做法还是比较容易的

令dp[i]表示打印完第$i$个单词的最小花费，$S[i]$表示$C[1]$到$C[i]$的前缀和，则转移方程为

[dp[i]=min{dp[j]+(S[i]-S[j])^{2}}+M]

我们想对这个进行优化，显然状态数是没有办法削减的，那么只能考虑：如何不枚举地得到最优转移？

要得到最优转移，首先我们要能够判断两个转移中哪个更优

假如我们分别从$j$、$k$（$j eq k$）转移来计算$dp[i]$，其中假设从j转移更优，则有

[dp[j]+(S[i]-S[j])^{2}<dp[k]+(S[i]-S[k])^{2}]

展开、移项后得到

[dp[j]-dp[k]+S[j]^{2}-S[k]^{2}<2S[i](S[j]-S[k])]

我们令

[f[i]=dp[i]+S[i]^{2}]

那么则有

[frac{f[j]-f[k]}{S[j]-S[k]}<2S[i], k<j]

[frac{f[j]-f[k]}{S[j]-S[k]}>2S[i], k>j]

（因为$f[i]$、$S[i]$均单调不减，所以除法后的变号能够确定）

左边跟物理中的斜率的表达式十分相似：表示横轴为$S$，纵轴为$f$的平面直角坐标系中，$j$点$(S[j],f[j])$到$k$点$(S[k],f[k])$的斜率

所以我们要找的最优转移j满足，对于所有的$1le k<j$，$j$点到$k$点的斜率小于$2S[i]$；对于所有的$j<k<i$，$j$点到$k$点的斜率大于$2S[i]$

或者说，过$j$作斜率为$2S[i]$的直线$L$，所有的$k eq j$均在$L$上方；即斜率为$2S[i]$的扫描线从上向下最后扫到的点

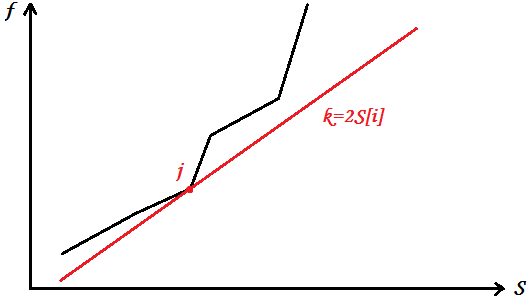
（随便画一下，大概是这个样子；这里不是很关键）

但是，现在离我们真正想出优化的方法还是有些距离的

现在我们考虑一个问题：我们能否根据一些点构成的形状，判断一个点能否成为最优转移？

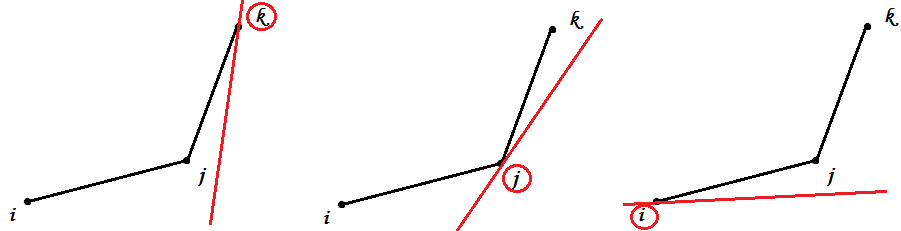
从简单的三点两线开始吧，不共线的时候共有两种情况（A）、（B）

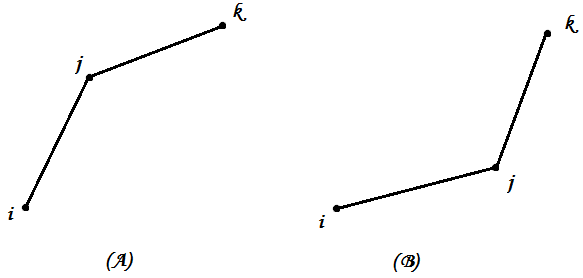
（A）（B）中两条直线斜率$k_{ij}$、$k_{jk}$的大小关系已经确定了，我们再带入斜率为$x$的直线来讨论一下（直观的方式是，作斜率为$x$的扫描线$L$）

（A）：

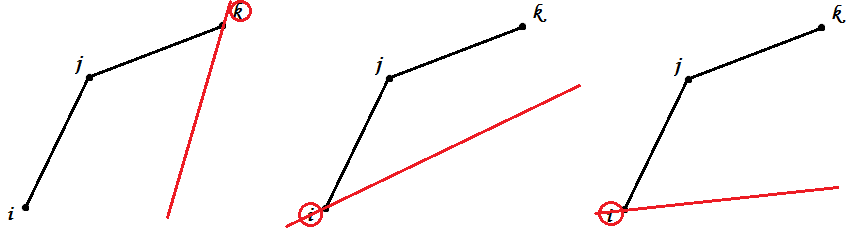
$k_{jk}<k_{ij}<x$：若过$k$作斜率为$x$的直线，则$i$、$j$均在直线上方，所以此时$k$最优

$k_{jk}<x<k_{ij}$：这里有两种可能，若$x<k_{ik}$则$i$最优（如第二个图）；若$x>k_{ik}$则$k$最优（这个情况没画）

$x<k_{jk}<k_{ij}$：若过$i$作斜率为$x$的直线，则$j$、$k$均在直线上方，所以此时$i$最优

总之，只要存在三点$i$、$j$、$k$（$i<j<k$）使得$j$在$ik$连线的上方，$j$就不可能是最优转移了

根据这条性质，所有可能是最优转移的点一定构成一个下凸的凸包，形状满足相邻线段斜率单调增（不过这里不需要什么凸包的知识啦，因为我也不会= =）

所以我们可以直接将不可能成为最优转移的$j$全部删去，得到这样的凸包

具体是怎么做的呢？

我们想加入i时，每次选择可用点的最后两个$q[sz-1]$、$q[sz]$，比较$q[sz-1]$与$q[sz]$连线、$q[sz]$与$i$连线的斜率$k_1$、$k_2$

• 若$k_1<k_2$，则直接将$i$加入可用点集$q$
• 若$k_1ge k_2$，则$q[sz]$是上凸的无用点，直接删去，并继续向前找

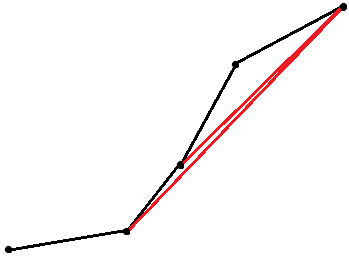
于是，（B）成为了删去无用点后、找最优点的简化版问题

（B）：

$k_{ij}<k_{jk}<x$：此时k最优

$k_{ij}<x<k_{jk}$：此时j最优

$x<k_{ij}<k_{jk}$：此时i最优

这里就能发现一个规律：$x$越大，最优转移的点越靠后

所以我们发现，因为$S[i]$是单调不减的，对于最优转移的点，其序号是只增不减的

而最优转移的点数目是$O(N)$规模的，即最优转移最多只会变化$n$次，这样均摊的转移就成功变为$O(1)$！

不过具体怎么找最优转移呢？

若上一个点的最优转移为可用点集中的第$j$个（即$q[j]$），那么我们计算$q[j]$、$q[j+1]$连线的斜率（这里对应的是斜率不等式中$k>j$的情况，不要搞混了）

• 若这个斜率小于$S[i]$，那么$q[j+1]$比$q[j]$更优，并继续比较$q[j+1]$、$q[j+2]$...
• 若这个斜率大于等于$S[i]$，那么$q[j+1]$不比$q[j]$更优，那么对于$i$，最优转移为$q[j]$

（如果这里不等式的右端不是单调不减的$S[i]$，而是一个任意的函数$g(i)$，那么每次选择最优转移点时，应当在当前可用点集中进行二分（比较$q[mid]$与$q[mid+1]$的斜率），这时转移是$O(logN)$的）

代码倒是挺短的...之前一直在看数据结构，突然有点不适应

在理论分析之外，还有些细节问题需要注意

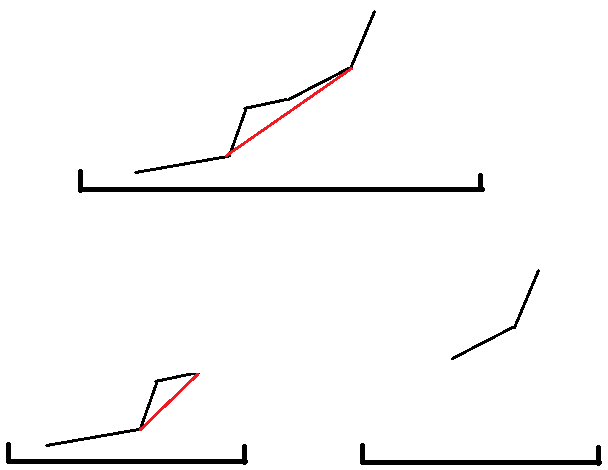
• 在动态维护下凸包时，有可能在删点后之前最优转移指针大于点集大小，此时应该将指针移到点集末尾（如此图）
• 比较斜率时可以开__int128后交叉相乘以避免除法（这样可以防止除$0$）
• 在选择最优的转移时，可以不用比较斜率，转而比较$dp$值会更方便（很实用）

#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;

typedef long long ll;
const int MAX=500005;

int n,m;
ll s[MAX];
ll dp[MAX];

int q[MAX];// Save available vertices

inline ll Calc(int j,int i)// Calculate dp[j]->dp[i]
{
    return dp[j]+(s[i]-s[j])*(s[i]-s[j])+m;
}

inline ll Up(int i,int j)
{
    return dp[i]-dp[j]+s[i]*s[i]-s[j]*s[j];
}

inline ll Down(int i,int j)
{
    return s[i]-s[j];
}

int main()
{
//    freopen("input.txt","r",stdin);
//    freopen("output.txt","w",stdout);
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            s[i]=s[i-1]+x;
        }
        
        q[1]=0;
        int j=1,sz=1;// Initially, 0 is in the queue
        for(int i=1;i<=n;i++)
        {
            while(j<sz && Calc(q[j],i)>Calc(q[j+1],i))
                j++;
            dp[i]=Calc(q[j],i);
            
            while(sz>1 && Up(q[sz],q[sz-1])*Down(i,q[sz])>=Up(i,q[sz])*Down(q[sz],q[sz-1]))
                sz--;
            q[++sz]=i;
            if(j>sz)
                j=sz;
        }
        printf("%lld
",dp[n]);
    }
    return 0;
}

---

慢慢补点题上来...

一道同样挺裸的题目：洛谷P3159（$HNoi2008$，玩具装箱）

这道题除了斜率式的不等号右边恶心一点以外，其余都跟例题差不多（甚至同样单调不减）

尽管$dp[i]$不一定单调不减，但是我们依然构造的是下凸包，只不过一开始斜率可以为负罢了

不过这题的斜率只能用$double$来比较了（通分必然爆$long$ $long$），有一个好消息是不存在$C_i=0$，所以可以放心地除

#include <cmath>
#include <cstring>
#include <cstdio>
using namespace std;

typedef long long ll;
const int MAX=50005;

int n,L;
ll s[MAX],dp[MAX];

int sz=1;
int q[MAX];

inline ll pow(ll x)
{
    return x*x;
}

inline ll Calc(int j,int i)
{
    return dp[j]+pow(i-j-1+s[i]-s[j]-L);
}

inline double Slope(int i,int j)
{
    return (dp[i]-dp[j]+pow(i+s[i])-pow(j+s[j]))/(double)(i-j+s[i]-s[j]);
}

int main()
{
//    freopen("input.txt","r",stdin);
    scanf("%d%d",&n,&L);
    for(int i=1;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        s[i]=s[i-1]+x;
    }
    
    int j=1;
    for(int i=1;i<=n;i++)
    {
        while(j<sz && Calc(q[j],i)>Calc(q[j+1],i))
            j++;
        dp[i]=Calc(q[j],i);
        
        while(sz>1 && Slope(q[sz],q[sz-1])>=Slope(i,q[sz]))
            sz--;
        q[++sz]=i;
        if(j>sz)
            j=sz;
    }
    printf("%lld
",dp[n]);
    return 0;
}

从洛谷上搜“斜率优化”找到的一题：CF 311B （$Cats$ $Transport$）

这题的数据有bug吧，出发时间竟然可以是负数...不要像我一样特判就好...

虽然最后的实现挺裸，但是前面要稍微做点准备

山之间走的时间和猫出现的时间都是假的，我们需要的时间是猫$i$在$t_i$时刻到达某山顶$d_i$反推的出发时间$a_i$，即在时间$a_i$从起点出发能正好捞到猫$i$

将这个时间$sort$一波，那么就可以转化成简单的二维$dp$了

令$dp[i][j]$表示派出第$i$个人、一直捞到猫$j$所需的最小代价，$a[j]$表示要正好捞猫$j$应该出发的时间，$s[j]$表示$a[j]$的前缀和，那么递推式为

[dp[i][j]=min{dp[i-1][k]+a[j]cdot (j-k)-(s[j]-s[k])}]

然后两个转移点$k$、$l$中，$k$更优的条件化简后是

[frac{dp[i-1][k]-dp[i-1][l]+s[k]-s[l]}{k-l}<a[j],l<k]

[frac{dp[i-1][k]-dp[i-1][l]+s[k]-s[l]}{k-l}>a[j],l>k]

剩下跟例题就一毛一样了...下一题一定不能找这样的裸题

（话说以前的Div1 B好难啊...现在的就不提了，连我都能做）

#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long ll;
const ll INF=1LL<<60;
const double eps=0.0000001;
const int MAXN=100005;
const int MAXM=100005;
const int MAXP=105;

int n,m,p;
int pre[MAXN];
int a[MAXM];
ll s[MAXM];

ll dp[MAXP][MAXM];
int q[MAXM];

inline ll Calc(int i,int j,int k)
{
    return dp[i-1][k]+a[j]*ll(j-k)-(s[j]-s[k]);
}

inline double Slope(int i,int j,int k)
{
    return double(dp[i-1][j]-dp[i-1][k]+s[j]-s[k])/(double)(j-k);
}

int main()
{
//    freopen("input.txt","r",stdin);
//    freopen("output.txt","w",stdout);
    scanf("%d%d%d",&n,&m,&p);
    for(int i=2;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        pre[i]=pre[i-1]+x;
    }
    for(int i=1;i<=m;i++)
    {
        int h,t;
        scanf("%d%d",&h,&t);
        a[i]=t-pre[h];
    }
    
    sort(a+1,a+m+1);
    for(int i=1;i<=m;i++)
        s[i]=s[i-1]+a[i];
    
    for(int i=1;i<=m;i++)
        dp[1][i]=Calc(1,i,0);
    for(int i=2;i<=p;i++)
    {
        int pnt=1,sz=1;
        for(int j=1;j<=m;j++)
        {
            while(pnt<sz && Calc(i,j,q[pnt])>Calc(i,j,q[pnt+1]))
                pnt++;
            dp[i][j]=min(INF,Calc(i,j,q[pnt]));
            
            while(sz>1 && Slope(i,q[sz],q[sz-1])>Slope(i,j,q[sz])-eps)
                sz--;
            q[++sz]=j;
            if(pnt>sz)
                pnt=sz;
        }
    }
    
    ll ans=INF;
    for(int i=1;i<=p;i++)
        ans=min(ans,dp[i][m]);
    printf("%I64d
",ans);
    return 0;
}

用假算法能过的一道题：洛谷P2305 （$NOI2014$，购票）

算法错没错？错了！值不值得练习？值得！（这里只是为了巩固斜率优化，在细节上已经是不简单的了）

如果没有$l\_v[i]$的限制条件，那么这道题就是一个树上的斜率优化$DP$

我们只要将当前路径（从$1$出发通过$i$的祖先到达$i$）上的节点依次压入一个栈，这时整个问题就变成了栈上的一维的$DP$了：所以我们只讨论一维的实现（但真正把树通过$dfs$拍成一维时，外部和内部的元素的关系会比较tricky）

问题是，加上了$l\_v[i]$的条件以后，假设第一个满足这个条件的节点为$j$，那么我们需要的下凸包是从$j$开始的；而我们之前的所有问题，下凸包都是从$1$开始的

这个博客里有比较清晰的图示，可以参考一下：zzyu5ds：NOI2014购票

那么应该怎么做呢？我们可以考虑从几个分开的下凸包中求出最优转移（说不定这种处理方法在哪题就是正解了呢）

我们这样存储下凸包：

开一颗线段树，其中每个节点都是一个$vector$（这样说比较容易懂，但最后会用大小为$NlogN$的数组实现），存储其对应区间中，以区间开头为起点的下凸包

这样的空间显然是$O(NlogN)$的：$O(N+2 imes frac{N}{2}+4 imes frac{N}{4}+...)$

如果我们想求从$j$开始的下凸包中的最优转移，我们可以先定位到覆盖区间是$[j,n]$的节点集合$S$（集合大小是$logN$级的）

这样就顺利得到了多个分开的下凸包；在每个下凸包中二分地找（对于此下凸包）最优的转移，$dp[i]$取这些转移中$DP$值的$min$

为什么这样的是对的呢？因为$[j,n]$整体的最优转移$k$，一定是某段下凸包的最优转移

用反证法：若$k$不是某下凸包的最优转移，则存在一条边，不仅大于凸包中$k$为起点的边的斜率、又满足最优斜率的性质；那么这条边一定也出现在$[j,n]$整体的凸包中，则$k$不是整体的最优转移

这样一来，查询的问题就解决了，单次是$O((logN)^2)$的；接下来是在$dfs$过程中执行插入和删除

插入：进入某树节点时，我们对$i$所在的全部$logN$个区间全部插入$i$

删除：离开某树节点时，我们对$i$所在的全部$logN$个区间全部恢复插入$i$前的状态（把插入时右端弹出的点记录一下，恢复时直接赋回去就行了）

我们的做法假在恢复状态——一个“菊花”形状的树能让我们总体的恢复节点数达到$O(N^2)$！

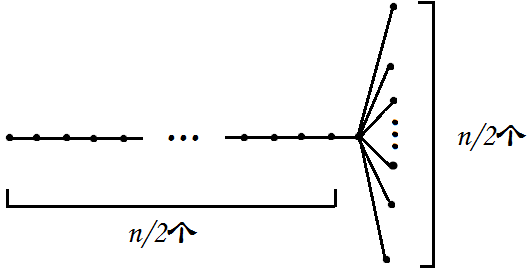
 好像很多用这种方法的人没有意识到....

（当然，想让左边$frac{n}{2}$个点的斜率单调增也不容易...但卡掉还是挺可能的）

#include <cstdio>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;

typedef long long ll;
const ll INF=1LL<<60;
const int N=200005;

int n,sz=1;
int fv[N];
ll sv[N],pv[N],qv[N],lv[N];
vector<int> v[N];

int stack[N];
ll sum[N],dp[N];

inline ll Calc(int i,int j)
{
    return dp[j]+(sum[i]-sum[j])*pv[i]+qv[i];
}

inline double Slope(int j,int k)
{
    return (dp[j]-dp[k])/double(sum[j]-sum[k]);
}

int arr[N*60];
int l[N<<2],r[N<<2];

int rsave[N][20];
int rcnt[N][20];
int rear=0;
int save[N*60];

inline void Insert(int k,int x,int a,int b,int d,int layer)
{
    if(a==b)
    {
        arr[++r[k]]=x;
        return;
    }
    
    rcnt[d][layer]=0;
    while(r[k]-l[k]>0 && Slope(arr[r[k]],arr[r[k]-1])>=Slope(x,arr[r[k]]))
        save[++rear]=arr[r[k]],rcnt[d][layer]++,r[k]--;
    rsave[d][layer]=r[k];//
    arr[++r[k]]=x;
    
    int mid=(a+b)>>1;
    if(d<=mid)
        Insert(k<<1,x,a,mid,d,layer+1);
    else
        Insert(k<<1|1,x,mid+1,b,d,layer+1);
}

inline void Recover(int k,int a,int b,int d,int layer)
{
    if(a==b)
    {
        r[k]=l[k]-1;
        return;
    }
    
    int mid=(a+b)>>1;
    if(d<=mid)
        Recover(k<<1,a,mid,d,layer+1);
    else
        Recover(k<<1|1,mid+1,b,d,layer+1);
    
    r[k]=rsave[d][layer];
    for(int i=1;i<=rcnt[d][layer];i++)
        arr[++r[k]]=save[rear--];
}

inline void getDP(int k,int p,int a,int b,int cur)
{
    if(a>=p)
    {
        int left=l[k],right=r[k],mid;
        while(left<right)
        {
            mid=(left+right)>>1;
            if(Calc(cur,arr[mid+1])<Calc(cur,arr[mid]))
                left=mid+1;
            else
                right=mid;
        }
        
        if(left==right)
            dp[cur]=min(dp[cur],Calc(cur,arr[left]));
        return;
    }
    
    int mid=(a+b)>>1;
    if(p<=mid)
        getDP(k<<1,p,a,mid,cur);
    getDP(k<<1|1,p,mid+1,b,cur);
}

inline void dfs(int x,int d)
{
    sum[x]=sum[fv[x]]+sv[x];
    stack[d]=x;
    
    int left=1,right=d-1,mid;
    while(left<right)
    {
        mid=(left+right)>>1;
        if(sum[x]-sum[stack[mid]]>lv[x])
            left=mid+1;
        else
            right=mid;
    }
    dp[x]=INF;
    getDP(1,left,1,sz,x);
    
    Insert(1,x,1,sz,d,1);
    for(int i=0;i<v[x].size();i++)
        dfs(v[x][i],d+1);
    Recover(1,1,sz,d,1);
}

int main()
{
//    freopen("testdata.in","r",stdin);
    int T;
    scanf("%d%d",&n,&T);
    while(sz<n)
        sz<<=1;
    for(int i=2;i<=n;i++)
    {
        scanf("%d%lld%lld%lld%lld",&fv[i],&sv[i],&pv[i],&qv[i],&lv[i]);
        v[fv[i]].push_back(i);
    }
    
    for(int i=1;i<=sz;i<<=1)//
        for(int j=0;j<i;j++)
            l[i+j]=r[i+j-1]+1,r[i+j]=l[i+j]+sz/i-1;
    for(int i=1;i<(sz<<1);i++)
        r[i]=l[i]-1;
    
    Insert(1,1,1,sz,1,1);
    for(int i=0;i<v[1].size();i++)
        dfs(v[1][i],2);
    
    for(int i=2;i<=n;i++)
        printf("%lld
",dp[i]);
    return 0;
}

（正解是树分治+斜率优化$DP$...还得啥时候再学一下orz）

---

暂时就把题目补到这里吧，以后遇到了有意思的题再放上来

牛客ACM 890J （$Wood Processing$）

这个写的真不熟...写的巨慢的主要原因还是dp式子一开始写错了

然后，用double比较的话一定要避免除$0$

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;

struct Plank
{
    int w,h;
    Plank(int a=0,int b=0)
    {
        w=a,h=b;
    }
};

typedef pair<int,int> pii;
typedef long long ll;
const int N=5005;
const int K=2005;
const ll INF=1LL<<60;
const double eps=0.000001;

int n,k;
Plank a[N];

inline bool cmp(Plank x,Plank y)
{
    if(x.h!=y.h)
        return x.h<y.h;
    return x.w<y.w;
}

int h[N];
ll sum[N],w[N];

ll dp[N][K];
int Q[N];

inline ll Calc(int i,int j,int k)
{
    return dp[k][j-1]+(sum[i]-sum[k])-(w[i]-w[k])*h[k+1];
}

inline ll Up(int i,int j)
{
    return dp[j][i-1]-sum[j]+w[j]*h[j+1];
}

inline double Slope(int i,int j,int k)
{
    return (Up(i,j)-Up(i,k))/double(h[j+1]-h[k+1]);
}

int main()
{
//    freopen("input.txt","r",stdin);
//    freopen("my.txt","w",stdout);
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&a[i].w,&a[i].h);
    
    sort(a+1,a+n+1,cmp);
    
    int tot=0;
    for(int i=1;i<=n;i)
    {
        tot++;
        sum[tot]=sum[tot-1];
        w[tot]=w[tot-1];
        h[tot]=a[i].h;
        
        int j=i;
        while(j<=n && a[j].h==a[i].h)
        {
            sum[tot]+=ll(a[j].w)*a[j].h;
            w[tot]+=a[j].w;
            j++;
        }
        i=j;
    }
    
    n=tot;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=k;j++)
            dp[i][j]=INF;
    
    for(int i=1;i<=n;i++)
        dp[i][1]=sum[i]-w[i]*h[1];
    
    for(int i=2;i<=k;i++)
    {
        int p=1,sz=1;
        Q[1]=0;
        for(int j=1;j<=n;j++)
        {
            while(p<sz && Calc(j,i,Q[p])+eps>Calc(j,i,Q[p+1]))
                p++;
            dp[j][i]=Calc(j,i,Q[p]);
            
            while(sz>1 && Slope(i,Q[sz],Q[sz-1])+eps>Slope(i,j,Q[sz]))
                sz--;
            Q[++sz]=j;
            if(p>sz)
                p=sz;    
        }
    }
    
    printf("%lld
",dp[n][k]);
    return 0;
}

（完）