预备知识
(A*)
A-star是什么?下面是百度的解释 >A-star算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。 F[i]=G[i]+H[i];
以上式子中(G[i])表示从起点到当前节点已经付出的代价,这个是准确的
(A*)算法最重要的是估价函数(H[i])的设计,(H[i])是估价函数,表示当前节点到终点的预计代价,当估价函数设为(0)时,就和普通的最短路没有区别,设从当前节点到终点的真实值为(X[i]),(H[i])越接近(X[i]),那么这个算法效率就越高,但需要注意一点。
我们要保证(H[i]<=X[i]),一旦大于,那么(A*)算法不能保证其正确性。
想必大家都很熟悉(BFS)了,在我的浅显的理解中,(A*)是对(BFS)的优化。
(A*)寻路
(Q:)假设有人想从(A)点移动到一墙之隔的(B)点,如下图,绿色的是起点(A),红色是终点(B),蓝色方块是中间的墙,假设走一格的代价为10,周围有八个方向可以移动,对角线的代价是(10sqrt 2),要求输出最优的路径。

第一个想法是用(BFS)(但我们是在讲(A*)啊喂)
然后我们还是要用(A*)的方法解决,和(BFS)很像,我们先开一个优先队列(按照F值从小到大排序),然后将起点周围的八个节点放入队列中,利用上面的公式(F[i]=G[i]+H[i]),这里不要求输出最优解,所以对角线用(14)近似即可,在格点图中,(H[i])通常使用当前节点与终点的曼哈顿距离,这样(H[i])也可以用(O(1))的复杂度求出。
现在我们再开两个数组(vis[i]、T[i]),(vis)标记了还在队列中的节点,(T[i])表示不用再被访问的节点
然后我们用一个数组存储当前节点从哪个节点转移而来,方便输出路径。当第一波操作完成后的情况是这样的。(左上角表示F值,左下角G值,右下角H值)
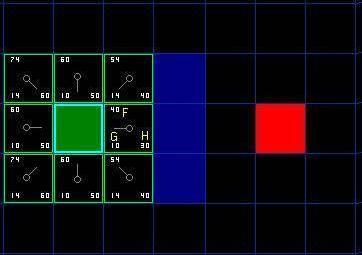
下面我们开始一系列操作
(1.)找出当前队列中的队首(其实就是(F)值最小的那个),将它取消标记在队列(vis)中,放入(T)中(一定要区分这两个数组,因为每次取的是最优解,这个节点一定不会被更优地更新了,所以它就像障碍物不用再访问了),然后将它扩展,重新计算出(G、H、F),设置父节点,并且将这个节点标记已经访问((vis)),放入队列。
(2.)如果遇到障碍物或在(T)中的节点,则跳过
(3.)如果遇到在(vis)的节点,检查转移后(G)值是否小于上次搜索到时的(G)值,如果是,那么更新这个节点的所有信息,重新计算,然后很重要的一点是重新设置父节点
好的,接下来不停进行这种操作,直到找到最终节点。

最后要做的,就是从终点开始访问父节点,将路径逆推出来就大功告成了,(A*)算法到此为止。
(Code)
什么你要(Code?)不好意思暂时没有