输入输出格式
输入格式:
第一行为(3)个整数,分别表示(a,b,n)的值
第二行至第(a+1)行每行为(b)个非负整数,表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。
输出格式:
仅一个整数,为(a*b)矩阵中所有(n*n)正方形区域中的最大整数和最小整数的差值”的最小值。
(Solution)
这个题竟然不是正经的(DP),本来尝试(DP)发现不可做(GG)。
结果最后还是看了题解,(woc?)单调队列 ,发现其实很简单
只要在每行做单调队列就形成了一个矩阵
然后对每一列做单调队列就可以形成最终的矩阵,在这个矩阵只需要统计(Sigma_i^{n-k+1}Sigma_j^{m-k+1}max(ans,Ymax[i][j]-Ymin[i][j]))
形象来说,对每行做单调队列,让(xmax[i][j])表示第(i)行中(j~j+k-1)的最大值
然后在将得出来的矩阵旋转,将还没有压缩的那一维和以上操作一样操作一番
以下是图解,转自(luogu)题解,其中(X[][])表示(xmax[][]),(x[][])表示(xmin[][]),(Y[][])表示(ymax[][]),(y[][])表示(ymin[][])。
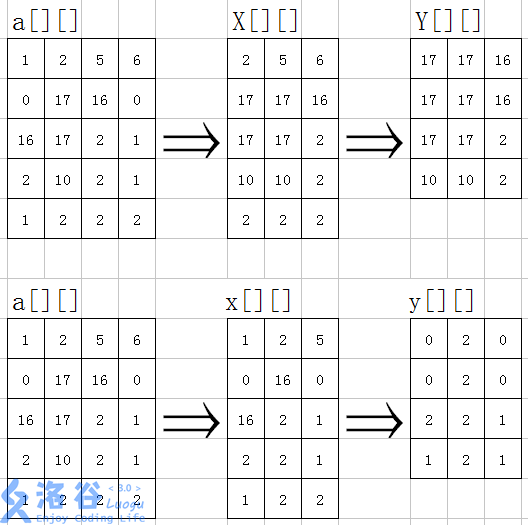
注意这里做单调队列是存储的权值的下标,权值是单调的。这是常规的单调队列写法,当然也可以开个结构体存权值+下标。
然后只需要从(2)开始做就行了,因为不存在(k=1)的情况
(Code)
#include<cstdio>
#include<iostream>
#define maxn 1010
#define re register
using namespace std;
int ans=0x7fffffff,front1,back1,front2,back2;
int a[maxn][maxn],q1[maxn],q2[maxn];
int xmax[maxn][maxn],xmin[maxn][maxn];
int ymax[maxn][maxn],ymin[maxn][maxn];
int n,m,k;
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(re int i=1;i<=n;++i)
for(re int j=1;j<=m;++j)
scanf("%d",&a[i][j]);
for(re int i=1;i<=n;++i)
{
front1=front2=back1=back2=q1[1]=q2[1]=1;
for(re int j=2;j<=m;++j)
{
while(a[i][j]>=a[i][q1[back1]]&&front1<=back1) back1--;
while(a[i][j]<=a[i][q2[back2]]&&front2<=back2) back2--;
back1++,back2++;
q1[back1]=j,q2[back2]=j;
while(j-q1[front1]>=k) front1++;
while(j-q2[front2]>=k) front2++;
if(j>=k) xmax[i][j-k+1]=a[i][q1[front1]],xmin[i][j-k+1]=a[i][q2[front2]];
}
}
for(re int j=1;j<=m-k+1;++j)
{
front1=front2=back1=back2=q1[1]=q2[1]=1;
for(re int i=2;i<=n;++i)
{
while(xmax[i][j]>=xmax[q1[back1]][j]&&front1<=back1) back1--;
while(xmin[i][j]<=xmin[q2[back2]][j]&&front2<=back2) back2--;
back1++,back2++;
q1[back1]=i,q2[back2]=i;
while(i-q1[front1]>=k) front1++;
while(i-q2[front2]>=k) front2++;
if(i>=k) ymax[i-k+1][j]=xmax[q1[front1]][j],ymin[i-k+1][j]=xmin[q2[front2]][j];
}
}
for(re int i=1;i<=n-k+1;++i)
{
for(re int j=1;j<=m-k+1;++j)
{
ans=min(ans,ymax[i][j]-ymin[i][j]);
}
}
printf("%d
",ans);
return 0;
}