学习笔记 贪心反悔的学习心得

写在卸载之前

这个东西是前两天刷题的时候刷到的

觉得很有意思 加上之前就已经做了几道这样的题

所以干脆学习了一下 发现这里面还挺大有学问的

正式开始

一般来讲 贪心是优先选取眼前最优解 然后一路向前 不存在返回操作

但是 正是因为贪心优先选取眼前最优解 导致我们容易错失全局最优解

从而导致一步错步步错

所以我们有的时候需要给贪心设置一个反悔操作 使得ta在认识到自己的错误之后可以选取更优解

这就是返回操作的机理

根据网上大牛的理论

贪心返回操作有两种形式

1.反悔自动机：设计一种策略 使得随便一种贪心都可以在最后得到最优解

具体实现是：我们每一次选取当前最优解 发现不对之后 则使用一些手段自动成为最优解 (一般来讲都是通过差值来实现的)

2.反悔堆：使用大根堆或者小根堆 维护当前已选择方案中对于答案贡献最小的(个人认为)

如果发现了更优的 则进行替换

我们还是上例题吧

1.【P1792 [国家集训队]种树】

判断无不无解我们就不说了

首先我们可以想到一种贪心 把所有的树按照价值从大到小排序 然后贪心选取就可以了

但是这是会被Hack的

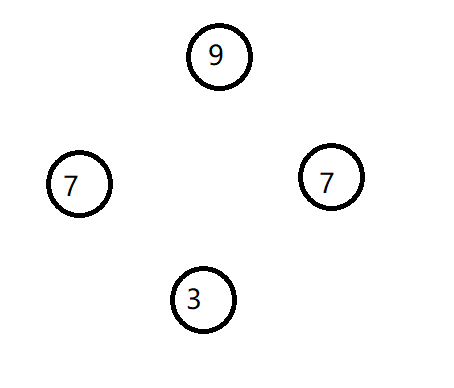
如图 排序之后我们可肯定优先选择9 然后这样的话我们最后求得的答案就是12

但是事实上最优答案是14

所以这里是涉及到了一个反悔操作

首先 我们知道 如果选择了一个点的话 后来返回只能是因为这个点左右两边的的点价值和大于这个点带来的价值

所以我们选择了9之后 再加入一个点价值为7+7-9

然后再修改一下左右两边的树

之后就成为了这样

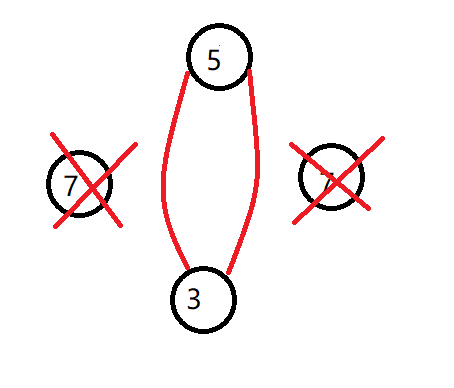
然后我们就可以不断维护最优解了

由于涉及到了每一次插入值且取最大值的操作 并且还涉及到了查询左右以及更更新操作

所以我们需要使用大根堆以及双向链表

CODE：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<queue>
#define N 200080
using namespace std;
priority_queue<pair<int,int> > que;
int n,m,ans;
bool vis[N];
struct Node
{
	int le,ri,val;
}num[N];
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n>>m;
	if(n<m*2)
	{
		printf("Error!");
		return 0;
	}
	for(int i=1;i<=n;++i)
	{
		cin>>num[i].val;
		if(i==1) num[i].le=n,num[i].ri=i+1;
		else if(i==n) num[i].le=i-1,num[i].ri=1;
		else num[i].le=i-1,num[i].ri=i+1;
		que.push(make_pair(num[i].val,i));
	} 
//	for(int i=1;i<=n;++i)
//	printf("(%d , %d)
",num[i].le,num[i].ri);
	for(int i=1;i<=m;++i)
	{
		while(vis[que.top().second]) que.pop();
		int x=que.top().first,y=que.top().second;que.pop();
		ans+=x;
//		printf("nnow %d at %d
",x,y);
		
		vis[num[y].le]=vis[num[y].ri]=1;
		num[y].val=num[num[y].le].val+num[num[y].ri].val-num[y].val;
//		printf("now now %d
",num[y].val,y);
		que.push(make_pair(num[y].val,y));
		num[y].le=num[num[y].le].le;
		num[y].ri=num[num[y].ri].ri;
		num[num[y].le].ri=y;
		num[num[y].ri].le=y;
		
	}
	cout<<ans<<endl; 
	return 0;
}

2.【P2748 [USACO16OPEN]Landscaping P】

这道题我之前就已经详解过了 【戳这里】

这里的话我们利用差值进行了自动更新 也就是反悔自动机

3.【P2949 [USACO09OPEN]Work Scheduling G】

这道题的贪心反悔就比较容易了

我们按照每个工作的截止时间进行排序

如果当前的工作已经误了截止时间的话 我们就跟之前已经选过的工作的最小价值进行比较 如果大于的话我们就取代了

可以使用小根堆进行维护

CODE：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define N 500080
using namespace std;
int n;long long ans;
struct Node
{
	int tim,val;
	friend bool operator < (const Node &A,const Node &B)
	{return A.tim==B.tim ? A.val>B.val:A.tim<B.tim;}
}e[N];
priority_queue<int,vector<int>,greater<int> > que;
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;++i)
	cin>>e[i].tim>>e[i].val;
	sort(e+1,e+n+1);
	for(int i=1;i<=n;++i)
	{
		if(que.size()>=e[i].tim)
		{
			if(que.top()>=e[i].val) continue;
			ans-=que.top();
			ans+=e[i].val;
			que.pop();
			que.push(e[i].val);
		}
		else
		{
			que.push(e[i].val);
			ans+=e[i].val;
		}
	}
	cout<<ans<<endl;
	return 0;
}

当然 一个篱笆三个桩 这题其实也不只有一种解法

我们可以考虑一下按照价值进行排序

对于所有的工作 时间越往左 越是公共的 所以我们需要尽量把他们往右安排

所以我们可以安排一个时间区间 对于一个截止时间为x的工作

然后我们查询[1,x]是否已经满了 如果没有慢的话 我们就二分一个最右的位置

单点修改 区间求和 这不是树状数组的节奏 ？

CODE：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<queue>
#define N 200080
using namespace std;
int n,cnt;long long anss;
int tre[N],res[N];
struct Node
{
	int tim,val,ti;
	friend bool operator < (const Node &A,const Node &B)
	{return A.val==B.val ? A.tim<B.tim : A.val>B.val;}
}num[N];
void add(int x,int d)
{for(;x<=n;x+=x&-x) tre[x]+=d;}
int query(int x)
{int tmp=0;for(;x;x-=x&-x) tmp+=tre[x];return tmp;}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;++i)
	cin>>num[i].tim>>num[i].val,res[i]=num[i].tim;
	sort(num+1,num+n+1);
	sort(res+1,res+n+1);cnt=unique(res+1,res+n+1)-res-1;
	for(int i=1;i<=n;++i)
	num[i].ti=lower_bound(res+1,res+cnt+1,num[i].tim)-res;
//	for(int i=1;i<=n;++i)
//	printf(" %d %d %d
",num[i].tim,num[i].val,num[i].ti);
	for(int i=1;i<=n;++i)
	{
		int tmp=query(num[i].ti);
		if(tmp==res[num[i].ti]) continue;
//		printf("now now now
");
		int le=1,ri=num[i].ti;
		while(le<ri)
		{
			int mid=(le+ri)>>1,tmps=query(mid);
			tmp=query(ri);
			if(tmp-tmps==res[ri]-res[mid]) ri=mid;
			else le=mid+1;
		}
//		printf("now at %d
",ans);
		anss+=(long long)num[i].val;add(le,1);
	
	}
	cout<<anss<<endl;
	return 0;
}

4.【P4053 [JSOI2007]建筑抢修】

这也算是一道比较经典的贪心反悔题了

我们按照截止时间排个序

然后对于当前已经误了的建筑 我们使用大根堆维护已经修好的最费时间的建筑 把最大的耗时跟当前加以比较 如果可以取代并且不误的就取代

CODE：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<queue> 
#define N 500080
using namespace std;
int n,ans;
long long nowall;
struct Node
{
	long long cost,tim;
	friend bool operator < (const Node &A,const Node &B)
	{return A.tim==B.tim ? A.cost<B.cost : A.tim<B.tim;}
}e[N];
priority_queue<long long> que; 
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;++i)
	cin>>e[i].cost>>e[i].tim;
	sort(e+1,e+n+1);
	for(int i=1;i<=n;++i)
	{
		if(nowall+e[i].cost>=e[i].tim)
		{
			if(que.top()<=e[i].cost) continue;
			nowall-=que.top();nowall+=e[i].cost;
			que.pop();
			que.push(e[i].cost);
		}
		else
		{
			++ans;
			nowall+=e[i].cost;
			que.push(e[i].cost);
		}
	}
	cout<<ans<<endl;
	return 0;
}

5.【CF865D Buy Low Sell High】

我i们考虑卖出一只股票的话 我们一定会选择之前买进的一只价格最小的股票

对于当前的股票b 我们假设之前买进的a 收入自然就是b-a

但是这不一定是最优的 所以我们考虑再次买进b(先不要在乎合不合理)

然后到了c的时候 我们再卖出的话 就是c-b+b-a=c-a

相当于我们买进了a 卖出了c

利用差值进行贪心的反悔 也就是反悔自动机

至于当前最小值 我们可以考虑使用一个小根堆进行维护

CODE:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define N 500080
using namespace std;
int n;long long ans;
priority_queue<int,vector<int>,greater<int> > que;
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1,x;i<=n;++i)
	{
		cin>>x;
		que.push(x);
		if(!que.empty()&&que.top()<x)
		{
			ans+=(long long)(x-que.top());
			que.pop();
			que.push(x);
			
		}
	}
	cout<<ans<<endl;
	return 0;
}

完结

具体的我只总结了这么多 接下来的话可能还再见到的