题目链接
题意分析
真是一道很有意思的题
由于没有通法可以使用 所以我们分成三种情况讨论
1.一维
我们把所有的点顺序排序 然后扫一遍
维护一个数轴
扫到一个点的时候 就把数轴[x-D,x+D]范围内的所有点统计一下 然后再把这个点加入到数轴中
由于是单点修改区间求和 所以我们可以使用树状数组
注意 由于范围问题 我们需要把所有需要用到的点离散化一下
2.二维
二维的话 就是曼哈顿距离了
我们可以考虑坐标系转化 曼哈顿距离转化为切比雪夫距离
然后把一维排序维护 另一维使用树状数组维护就可以了
3.三维
这就比较麻烦了
但是考虑坐标的极限是[1,75] 我们就可以搞一些事情了
网上大佬的高级方法咱不会 所以只能用点小暴力了
我直接使用了三维曼哈顿转切比雪夫
懒得直接手打了 我就直接上图吧
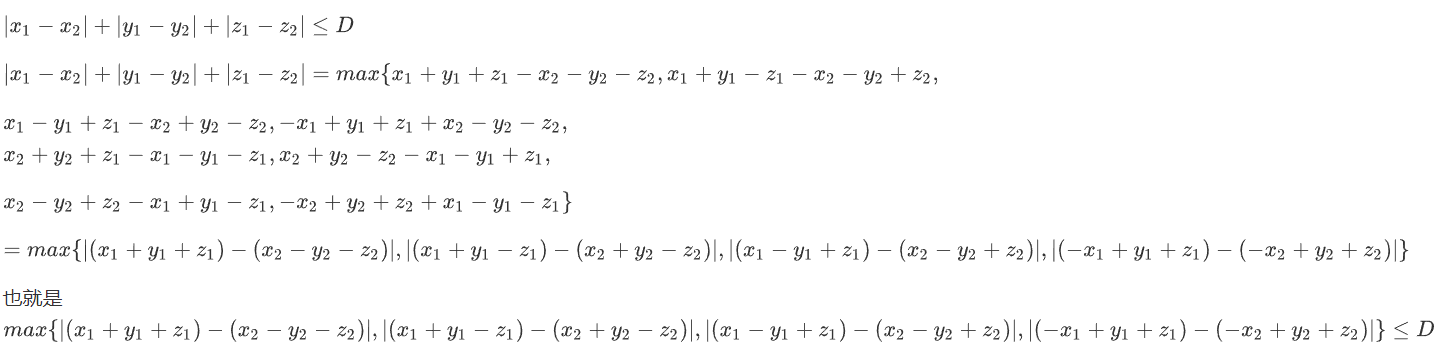
第一维我直接排序维护 然后剩下的三维树状数组维护
对你没有听错 就是三维树状数组 就是按照三维前缀和维护就可以了
原始的值域是[-m,2m] 为了防止负下标 维护成了[0,3m]
也省得的离散化了
CODE:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#define N 300080
#define M 230
using namespace std;
int B;
int n,dm,m,cnt;
int tre[N],res[N];
int tree[M][M][M];
struct Node1
{
int le,ri,at;
}e1[N];
struct Node2
{
int xx,yy,le,ri,at;
friend bool operator < (const Node2 &A,const Node2 &B)
{return A.xx<B.xx;}
}e2[N];
struct Node3
{
int xx,yy,zz,kk;
friend bool operator < (const Node3 &A,const Node3 &B)
{return A.kk<B.kk;}
}e3[N];
long long ans;
int query(int x)
{int tmp=0;for(;x>0;x-=x&-x) tmp+=tre[x];return tmp;}
void add(int x,int d)
{for(;x<=cnt;x+=x&-x) tre[x]+=d;}
void update(int x,int y,int z,int d)
{//三维树状数组的修改
for(int i=x;i<=3*m;i+=i&-i)
for(int j=y;j<=3*m;j+=j&-j)
for(int k=z;k<=3*m;k+=k&-k)
tree[i][j][k]+=d;
}
int qury(int x,int y,int z)
{//三维树状数组的查询
int tmp=0;
x=min(x,3*m);
y=min(y,3*m);
z=min(z,3*m);
for(int i=x;i>0;i-=i&-i)
for(int j=y;j>0;j-=j&-j)
for(int k=z;k>0;k-=k&-k)
tmp+=tree[i][j][k];
return tmp;
}
int getsum(int la,int ra,int lb,int rb,int lc,int rc)
{//三维前缀和的操作
int tmp1,tmp2,tmp3;
tmp1=qury(ra,rb,rc)-qury(la-1,rb,rc)-qury(ra,lb-1,rc)-qury(ra,rb,lc-1);
tmp2=qury(la-1,lb-1,rc)+qury(la-1,rb,lc-1)+qury(ra,lb-1,lc-1)-qury(la-1,lb-1,lc-1);
return tmp1-tmp2;
}
int main()
{
scanf("%d",&B);
if(B==1)//一维情况
{
scanf("%d%d%d",&n,&dm,&m);
for(int i=1,x;i<=n;++i)
{
scanf("%d",&x);
e1[i]=(Node1){x-dm,x+dm,x};
res[i*3-2]=x-dm;
res[i*3-1]=x+dm;
res[i*3]=x;
}
sort(res+1,res+3*n+1);cnt=unique(res+1,res+3*n+1)-res-1;
for(int i=1;i<=n;++i)
{
e1[i].le=lower_bound(res+1,res+cnt+1,e1[i].le)-res;
e1[i].ri=lower_bound(res+1,res+cnt+1,e1[i].ri)-res;
e1[i].at=lower_bound(res+1,res+cnt+1,e1[i].at)-res;
}
for(int i=1;i<=n;++i)
{
ans+=(long long)(query(e1[i].ri)-query(e1[i].le-1));
add(e1[i].at,1);
}
printf("%lld
",ans);
}
if(B==2)//二维情况
{
scanf("%d%d%d",&n,&dm,&m);
for(int i=1,x,y;i<=n;++i)
{
scanf("%d%d",&x,&y);
e2[i].xx=x+y;e2[i].yy=x-y;
e2[i].le=e2[i].yy-dm;e2[i].ri=e2[i].yy+dm;
e2[i].at=e2[i].yy;
res[i*3-2]=e2[i].le;
res[i*3-1]=e2[i].ri;
res[i*3]=e2[i].at;
}
sort(res+1,res+3*n+1);cnt=unique(res+1,res+3*n+1)-res-1;
sort(e2+1,e2+n+1);
for(int i=1;i<=n;++i)
{
e2[i].le=lower_bound(res+1,res+cnt+1,e2[i].le)-res;
e2[i].ri=lower_bound(res+1,res+cnt+1,e2[i].ri)-res;
e2[i].at=lower_bound(res+1,res+cnt+1,e2[i].at)-res;
}
for(int i=1,tail=1;i<=n;++i)
{
while(tail<i&&e2[i].xx-e2[tail].xx>dm)
{
add(e2[tail].at,-1);
++tail;
}
ans+=(long long)(query(e2[i].ri)-query(e2[i].le-1));
add(e2[i].at,1);
}
printf("%lld
",ans);
}
if(B==3)//三维情况
{
scanf("%d%d%d",&n,&dm,&m);
for(int i=1,x,y,z;i<=n;++i)
{
scanf("%d%d%d",&x,&y,&z);
e3[i]=(Node3){x+y-z+m,x+z-y+m,z+y-x+m,x+y+z};
}
sort(e3+1,e3+n+1);
for(int i=1,tail=1;i<=n;++i)
{
while(tail<i&&e3[i].kk-e3[tail].kk>dm)
{
update(e3[tail].xx,e3[tail].yy,e3[tail].zz,-1);
++tail;
}
ans+=(long long)getsum(e3[i].xx-dm,e3[i].xx+dm,e3[i].yy-dm,e3[i].yy+dm,e3[i].zz-dm,e3[i].zz+dm);
update(e3[i].xx,e3[i].yy,e3[i].zz,1);
}
printf("%lld
",ans);
}
return 0;
}