本文将同步发布于:
题目
题意简述
给你牌数为 (m+1) 的牌堆,其中第 (m+1) 张为固定的牌,每张牌用一个非负整数 (omega) 表示,表示打出这张牌可以继续抽 (omega) 张牌。
给出所有 (omegageq 1) 的牌的数量 (n) 和 (omega_i),请你求出在总共 (m!) 种情况中,有多少种情况可以抽到最后一张牌(固定的牌)。
题解
数学转化
考虑用数学语言表示题目,即转化合法牌堆需要满足的条件。
定义 ( exttt{sum}_i=sumlimits^{i}_{j=1}omega_j),那么我们可以转化题意条件为
意思就是,我在打出第 (i) 张特殊牌之后收集的牌的总数量要大于等于打出的数量,这样才合法。
考虑重新定义 ( exttt{sum}_i=sumlimits^{i}_{j=1}(omega_j-1)),那么我们可以转化题意条件为
也就是说,我们将 (omega_i-1) 看作一个新的数列,原数列合法当且仅当新数列的前缀和均为非负整数。
激发联想
一个整数数列的前缀和可以激发我们的联想,使得我们联想到 Raney 引理。
Raney 引理:设整数序列 (A={a_1,a_2,cdots,a_n}),且部分和 (S_k=a_1+cdots+a_k),序列中所有的数字的和 (S_n=1),则在 (A) 的 (n) 个循环表示中,有且仅有一个序列 (B),满足 (B) 的任意部分和 (S_i) 均大于零。
我们先来证明一下 Raney 引理。
考虑对任意一个整数数列做出前缀和图像。
下面以 (a=[1,3,-4,1]) 为例。
作一条斜率为 (frac{1}{n}) 的直线,将其平移到与图像下相切。
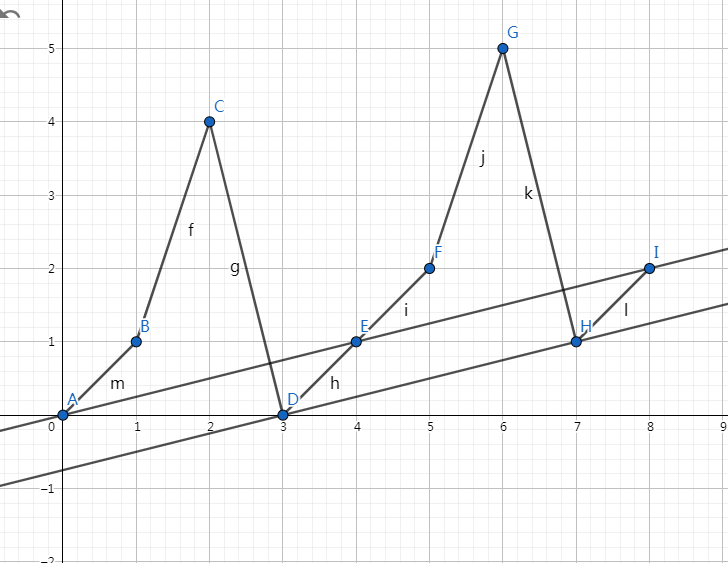
- 充分性:不难发现,如果我们以切点为循环位移的终点(它后一个点为数列的第一项),构造出来的数列一定符合条件;
- 必要性:如果不相切,必定存在其他的交点,考虑到数列中都是整数,交点一定满足纵坐标小于等于切点,做差后等价于前缀和小于等于零,不合法。
Raney 引理得证。
进一步地转化
现在的问题是我们将 (omega_i-1) 看作一个新的数列,原数列合法当且仅当新数列的前缀和均为非负整数。这与 Raney 引理的形式很不一样。
我们发现当前的数列有几个特征:
- 总和为 (0),但 Raney 引理要求为 (1);
- 我们要求前缀和大于等于 (0),但 Raney 引理要求大于 (0)。
冷静思考可以构造出一种优雅的转化方式:给数列末端加上一个 (-1)。然后整个数列倒过来,所有数符号取反。
这样就完成了上述两个特征的转化,在这一步转化中,我们将数列的和转成了 (1),并且前缀和必须大于 (0)。
前缀和转化的具体过程:
- 前缀和大于等于 (0),且数列总和为 (0),说明数列的后缀和小于等于 (0);
- 在数列末端插入 (-1),新数列的后缀和小于等于 (-1);
- 倒转数列,新数列的前缀和小于等于 (-1);
- 符号取反,不等号方向改变,新数列的前缀和大于等于 (1),即大于 (0)。
组合数学求答案
Raney 引理指引我们,合法的方案数等于新数列原排列的方案数,这是因为一个圆排列恰好对应一组循环同构的排列。
所以我们只需要求出经过上面一系列转化后的数列的圆排列个数即可,答案为 (frac{(m+1)!}{m+1}=m!)。
可是这样对吗?不对。
因为我们在数列中插入了一个 (-1)(后变为 (1)),而根据推理,原数列中 (omega_i=0) 的数列在新数列中的值也为 (1),它们之间的排列重复计算,因此应该用除法原理去除。
原来共有 (m-n) 个 (0),对应排列数为 ((m-n)!),而新数列中对应 (1) 的个数为 (m-n+1),所以答案应当除以 (m-n+1)。
总而言之,答案为 (frac{m!}{m-n+1})。
参考程序
#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
const int mod=998244353;
int n;
int main(void){
scanf("%d",&n);
reg int m=0;
for(reg int i=1;i<=n;++i){
static int w;
scanf("%d",&w);
m+=w;
}
reg int ans=1;
for(reg int i=1;i<=m;++i)
if(m-n+1!=i)
ans=1ll*ans*i%mod;
printf("%d
",ans);
return 0;
}