「题解」agc031_c Differ by 1 Bit

本文将同步发布于：

• 洛谷博客；
• csdn；
• 博客园；
• 简书；

题目

题目链接：洛谷 AT4693、AtCoder agc031_c。

题意概述

给定三个数 (n,a,b)，求一个 (0sim 2^n-1) 的排列满足下列三个条件：

• (p_1=a)；
• (p_{2^n}=b)；
• (operatorname{popcount}(p_ioplus p_{i+1})=1)，其中 (oplus) 表示按位异或。

请你判定是否可以构造并输出方案（若可以）。

题解

启发式的画图

直接考虑这个问题，似乎有些困难？

我们先用简单的语言，将它转化为一个图论问题。

图论转化

如果两个整数 (a,bin[0,2^n))，满足 (operatorname{popcount}(aoplus b)=1)，那么我们就在 (a,b) 之间连一条边。

那么问题转化为了给定起点与终点，求一条长度为 (2^n) 的简单路径。

---

转化成了图论问题，我们肯定要用几何直观来看看这个图到底是什么样子，采用画图工具 Graph Editor，取 (n=2,3) 时：

图片 (n=2)：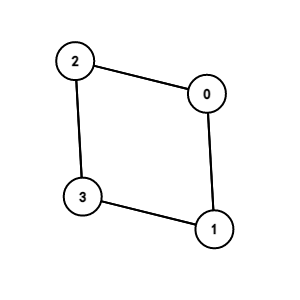

图片 (n=3)：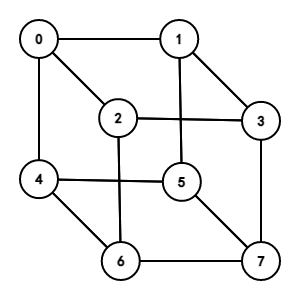

这提醒我们，整个图将会形成一个 (n) 维立方体。

具体地，我们考虑证明这件事，非常简单，换个角度即可。我们将一个二进制数各位上的数分开，看作各个维度的坐标值，例如 (0=(00)_2 o (0,0),2=(10)_2 o (1,0))。那么我们不难得到此结论。

熟练解决图论问题

我们不难发现，这个图是一个二分图，其中左部点编号对应的二进制数中 (1) 的个数为偶数，右部点编号对应的二进制数中 (1) 的个数为奇数。

我们由此得到结论，如果存在答案，那么 (operatorname{popcount}(aoplus b)equiv 1pmod 2)。

这个条件对解的必要性已经得到证明，下面我们通过构造来证明其充分性。

构造与递推

首先为了化简问题，我们不难发现从 (a) 走到 (b) 等价于从 (0) 走到 (aoplus b)，这是因为异或的自反律与交换律，即 (p_ioplus xoplus p_{i+1}oplus x=p_ioplus p_{i+1})。

对于 (n) 维立方体，它一定是由两个 (n-1) 维立方体上下拼接而成。

因此，我们考虑用类似数学归纳法的方式进行构造。

我们具有归纳基础，因为显然我们会 (n=1) 时的情况（一条线段从 (0) 走到 (1)）；

我们考虑如何通过 (n-1) 维的方案构造 (n) 维的方案，我们决定分类讨论：

• 根据上面的理论，我们分类讨论终点的位置（起点为 (0)）；
• 终点 (t) 与起点在不同的层：我们找到一条合法的从起点走 (n-1) 维空间到达 (x) 的方案，然后 (x) 走到另一层对应的点 (x')，再在 (n-1) 维空间中从 (0) 走到 (toplus x') 的方案，(x) 可任取；
• 终点 (t) 与起点在同一层：我们直接从 (0) 走到 (t)，然后把路径从路径中任意两个相邻点之间直接分割开来，在中间插入一个下层的 (n-1) 维的路径。

上面的文字叙述可能有点难懂，我们画个三维空间的图：

第一种情况：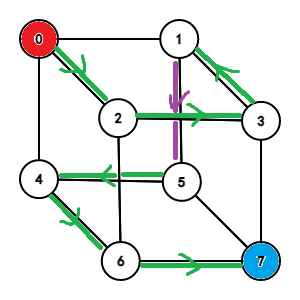

第二种情况：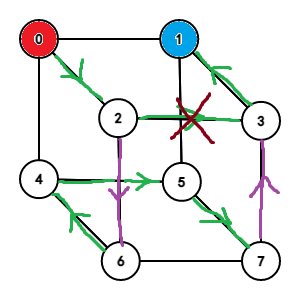

至此，我们用构造的方法证明了条件的充分性，可解决本题。

时间复杂度为 (T(n)=2T(n-1)+Theta(2^n))，分析可知为 (Theta(2^nn))。

参考程序

参考程序中情况一选取 (x=1)，情况二选取起点和路径的第二个点。

__builtin_parity(x) 表示求 (x) 的二进制表示中 (1) 的个数的奇偶性，奇数为 (1)，偶数为 (0)。

#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
#define flush() (fwrite(wbuf,1,wp1,stdout),wp1=0)
#define putchar(c) (wp1==wp2&&(flush(),0),wbuf[wp1++]=c)
static char wbuf[1<<21];int wp1;const int wp2=1<<21;

inline void write(reg int x){
	static char buf[32];
	reg int p=-1;
	if(!x) putchar('0');
	else while(x) buf[++p]=(x%10)^'0',x/=10;
	while(~p) putchar(buf[p--]);
	return;
}

inline void writeln(const char *s){
	while(*s) putchar(*(s++));
	putchar('
');
	return;
}

const int MAXN=17;

inline void solve(reg int x,reg int a,reg int ans[]){
	if(!x)
		ans[0]=0;
	else if(x==1)
		ans[0]=0,ans[1]=1;
	else{
		reg int val=1<<(x-1);
		if(a&val){
			solve(x-1,1,ans),solve(x-1,a^(val+1),ans+val);
			for(reg int i=val;i<(1<<x);++i)
				ans[i]=ans[i]^(val+1);
		}
		else{
			solve(x-1,a,ans),solve(x-1,ans[1],ans+val);
			for(reg int i=val;i<(1<<x);++i)
				ans[i]=ans[i]^val;
			static int tmp[1<<MAXN];
			tmp[0]=ans[0];
			for(reg int i=0;i<val;++i)
				tmp[i+1]=ans[i+val];
			for(reg int i=val+1;i<(1<<x);++i)
				tmp[i]=ans[i-val];
			for(reg int i=0;i<(1<<x);++i)
				ans[i]=tmp[i];
		}
	}
	return;
}

int n,A,B;
int ans[1<<MAXN];

int main(void){
	scanf("%d%d%d",&n,&A,&B);
	B^=A;
	if(__builtin_parity(B)){
		writeln("YES");
		solve(n,B,ans);
		reg int U=(1<<n)-1;
		for(reg int i=0;i<=U;++i)
			write(ans[i]^A),putchar(i==U?'
':' ');
	}
	else
		writeln("NO");
	flush();
	return 0;
}