打模拟赛 ⇨ 写主席树TLE了 ⇨ 看正解是可持久化平衡树 ⇨ 原来我还没写过可持久化平衡树 ⇨ 现学
# 平衡树的可持久化
可持久化就是「不修改原始信息,将新版本的信息新建节点储存」。
可持久化我们熟悉啥?众所周知的线段树可以可持久化,因为每次修改只会改一条从根到叶子的链,树高是 (mathcal{O}(log n)) 的,所以每次只会增加这么多点数。
那平衡树似乎也是这么个道理,树高是 (mathcal{O}(log n)) 的,每次也是修改根到叶子的一条链。
但是有个问题,其实线段树方便可持久化的另一原因是 它的结构(树形)不会改变。
虽然并不是说树形改变就不能可持久化(反正听说 splay 什么也是可以可持久化的),但若是有旋转操作的平衡树,可持久化就相当麻烦。于是我们说的可持久化平衡树,大多数时候就是 非旋Treap 的可持久化。
# 可持久化非旋Treap
非旋 Treap 最重要的两个操作当然就是 split 和 merge。其他操作都不会 直接地改变树形,因此我们只考虑 split 和 merge 的可持久化,以及与之密切相关的 insert 和 delete 操作。
- split & merge
先看 split,这个比较简单,因为不能改变原始信息 —— 也就是不能直接把根 (u) 给拆开。那么我们就复制一个节点 (u'),把 (u') 拆开即可。伪代码如下:
点击展开/折叠伪代码
然后是 merge,其实 merge 本身可持久化也非常简单,只需要把合并得到的节点新建节点就可以了。问题在于 —— 我们真的需要对 merge 新建节点吗?
在比较常见的平衡树操作中,split 和 merge 往往是成对出现的,一般就是把原树 split 过后进行一些操作再 merge 回来。如果 split 和 merge 都新建节点,那么节点数就会有 ( imes2) 的常数。
关于这一点,我比较认同这篇博客:可持久化平衡树详解及实现方法分析。我个人的理解如下:
- 由于 merge 和 split 成对出现,那么 merge 时的版本应该和 split 的版本是一样的(都是「当前版本」);
- 如果 merge 时合并的节点都是当前版本的节点,那么就不需要新建点。
我们不妨观察 split 的代码实现。函数返回的是当前这棵树按照键值 (key) 分成的两棵树的根节点,而这些根节点都是我们新建的。
简称 split 得到的 (le key) 的树为「左树」,另一棵为「右树」。
结合下图可以发现,左树最右侧的一条链 和 右树最左侧的一条链 都是新建的节点:
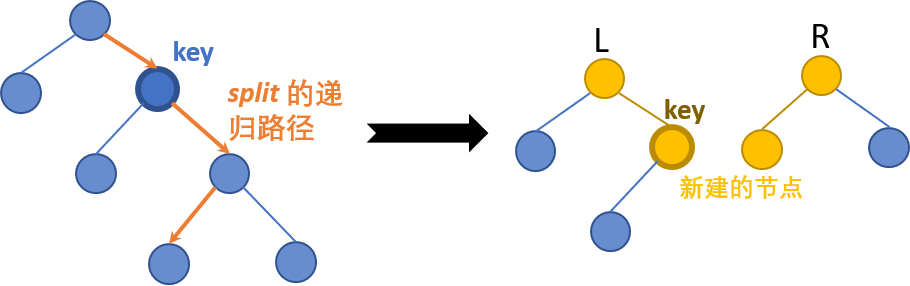
如果 merge 的时候也是合并的这些新建的节点就好了。
若将相同键值储存在同一个节点上记录 count,这样 split 和 merge 的方案是唯一的,所以 merge 的一定也是这些节点。
这里其实有一点不是很理解,就是把相同键值也分开存会有什么问题……如果有读者知道,欢迎在评论区中提出
- insert & delete
注意到我们把相同键值储存在同一个节点中了,insert 时就不能直接新建节点 (key),把原树按 (key) split 开再 merge 回去。
于是先直接在平衡树上找到 (key) 这个点(如果有的话),然后将根到这个节点的路径全部新建节点,更新 count 和 size。
否则就按键值 split 开,新建节点 (key) 通过 merge 插入在左树和右树中间。新建的节点当然也是「当前版本」的节点,根据上面的论证,merge 不需要新建节点。
delete 同理,先找 (key) 对应的节点,若存在大于等于两个 (key),则和 insert 一样,复制一份根到该节点的链更新 count 和 size。否则删除过后这个节点就不见了,将原树 split 两遍就可以把这个节点单独挑出来,剩下的直接 merge 就可以了。
# 源代码
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
inline int rin(int &r){
int b=1,c=getchar();r=0;
while(c<'0' || '9'<c) b=c=='-'?-1:b,c=getchar();
while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
return r*=b;
}
const int N=5e5+10;
#define con(type) const type &
typedef pair<int,int> pii;
struct Node{
int nxt[2],cnt,key,siz,fix;
inline int& operator [](con(int)i){return nxt[i];}
};
struct Treap{
Node nod[N*40];
int ncnt,rt[N];
int copyNode(con(int)from){
int p=++ncnt;
nod[p]=nod[from];
return p;
}
int newNode(con(int)key){
int p=++ncnt;
nod[p][0]=nod[p][1]=0;
nod[p].cnt=nod[p].siz=1;
nod[p].key=key;
nod[p].fix=rand();
return p;
}
void pushUp(con(int)u){nod[u].siz=nod[nod[u][0]].siz+nod[nod[u][1]].siz+nod[u].cnt;}
pii splitKey(con(int)u,con(int)key){
pii ret(0,0);
if(!u) return ret;
int nu=copyNode(u);
if(nod[nu].key<=key){
ret=splitKey(nod[nu][1],key);
nod[nu][1]=ret.first,ret.first=nu;
}
else{
ret=splitKey(nod[nu][0],key);
nod[nu][0]=ret.second,ret.second=nu;
}
pushUp(nu);
return ret;
}
int ina_merge(con(int)u,con(int)v){
if(!u || !v) return u|v;
if(nod[u].fix<nod[v].fix){
nod[u][1]=ina_merge(nod[u][1],v),pushUp(u);
return u;
}
else{
nod[v][0]=ina_merge(u,nod[v][0]),pushUp(v);
return v;
}
}
int getCount(con(int)u,con(int)key){
if(!u) return 0;
if(nod[u].key==key) return nod[u].cnt;
if(key<nod[u].key) return getCount(nod[u][0],key);
else return getCount(nod[u][1],key);
}
int directEdit(con(int)u,con(int)key,con(int)typ){
if(nod[u].key==key){
int nu=copyNode(u);
nod[nu].cnt+=typ,pushUp(nu);
return nu;
}
if(key<nod[u].key){
int nu=copyNode(u);
nod[nu][0]=directEdit(nod[nu][0],key,typ);
pushUp(nu);
return nu;
}
else{
int nu=copyNode(u);
nod[nu][1]=directEdit(nod[nu][1],key,typ);
pushUp(nu);
return nu;
}
}
void ina_insert(int &urt,con(int)vrt,con(int)key){
if(getCount(vrt,key)){
urt=directEdit(vrt,key,1);
return;
}
pii tmp=splitKey(vrt,key);
urt=ina_merge(ina_merge(tmp.first,newNode(key)),tmp.second);
}
void ina_delete(int &urt,con(int)vrt,con(int)key){
if(getCount(vrt,key)>1){
urt=directEdit(vrt,key,-1);
return;
}
pii tmp1=splitKey(vrt,key),tmp2=splitKey(tmp1.first,key-1);
urt=ina_merge(tmp2.first,tmp1.second);
}
// the number of elements strictly smaller than 'key'
int getRank(con(int)u,con(int)key){
if(!u) return 0;
if(nod[u].key==key) return nod[nod[u][0]].siz;
if(key<nod[u].key) return getRank(nod[u][0],key);
else return getRank(nod[u][1],key)+nod[nod[u][0]].siz+nod[u].cnt;
}
int getIndex(con(int)u,con(int)rnk){
if(nod[nod[u][0]].siz>=rnk) return getIndex(nod[u][0],rnk);
if(nod[nod[u][0]].siz+nod[u].cnt>=rnk) return nod[u].key;
return getIndex(nod[u][1],rnk-nod[nod[u][0]].siz-nod[u].cnt);
}
// the smallest element strictly greater than 'key'
int getNext(con(int)u,con(int)key){
if(!u) return -1;
if(key<nod[u].key){
int res=getNext(nod[u][0],key);
if(~res) return res;
return nod[u].key;
}
else return getNext(nod[u][1],key);
}
// the largest element strictly smaller than 'key'
int getPrev(con(int)u,con(int)key){
if(!u) return -1;
if(key>nod[u].key){
int res=getPrev(nod[u][1],key);
if(~res) return res;
return nod[u].key;
}
else return getPrev(nod[u][0],key);
}
// guard index
Treap(){rt[0]=ina_merge(newNode(int(1-(1ll<<31))),newNode(int((1ll<<31)-1)));}
inline int& operator [](con(int)i){return rt[i];}
void debug(con(int)u){
if(!u) return;
debug(nod[u][0]);
printf(" index %d * %d
",nod[u].key,nod[u].cnt);
debug(nod[u][1]);
}
}tr;
int n;
int main(){
// freopen("input.in","r",stdin);
rin(n);
for(int i=1,iver,cmd,key;i<=n;i++){
rin(iver),rin(cmd),rin(key);
switch(cmd){
case 1: tr.ina_insert(tr[i],tr[iver],key);break;
case 2: tr.ina_delete(tr[i],tr[iver],key);break;
case 3: printf("%d
",tr.getRank(tr[i]=tr[iver],key));break;
case 4: printf("%d
",tr.getIndex(tr[i]=tr[iver],key+1));break;
case 5: printf("%d
",tr.getPrev(tr[i]=tr[iver],key));break;
case 6: printf("%d
",tr.getNext(tr[i]=tr[iver],key));break;
}
// printf("version %d
",i),tr.debug(tr[i]);
}
return 0;
}