线性回归

线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

• 特点：只有一个自变量的情况称为单变量回归，大于一个自变量情况的叫做多元回归

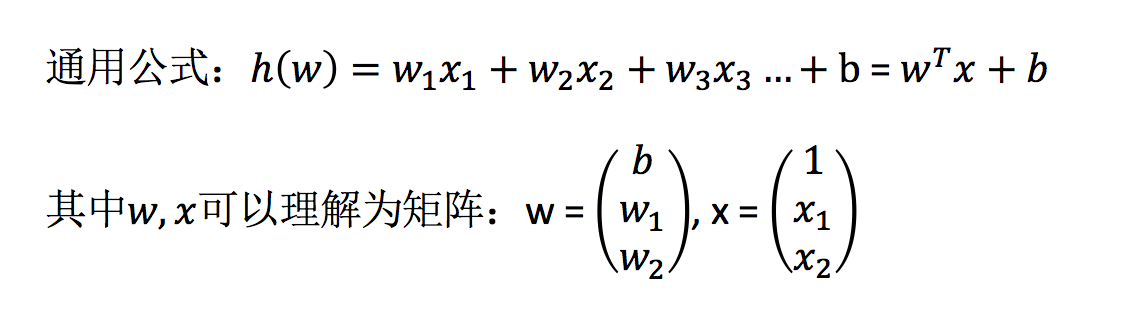
损失函数

总损失定义为：

• y_i为第i个训练样本的真实值
• h(x_i)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！！！

优化算法

如何去求模型当中的W，使得损失最小？（目的是找到最小损失对应的W值）

线性回归经常使用的两种优化算法

• 正规方程

理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

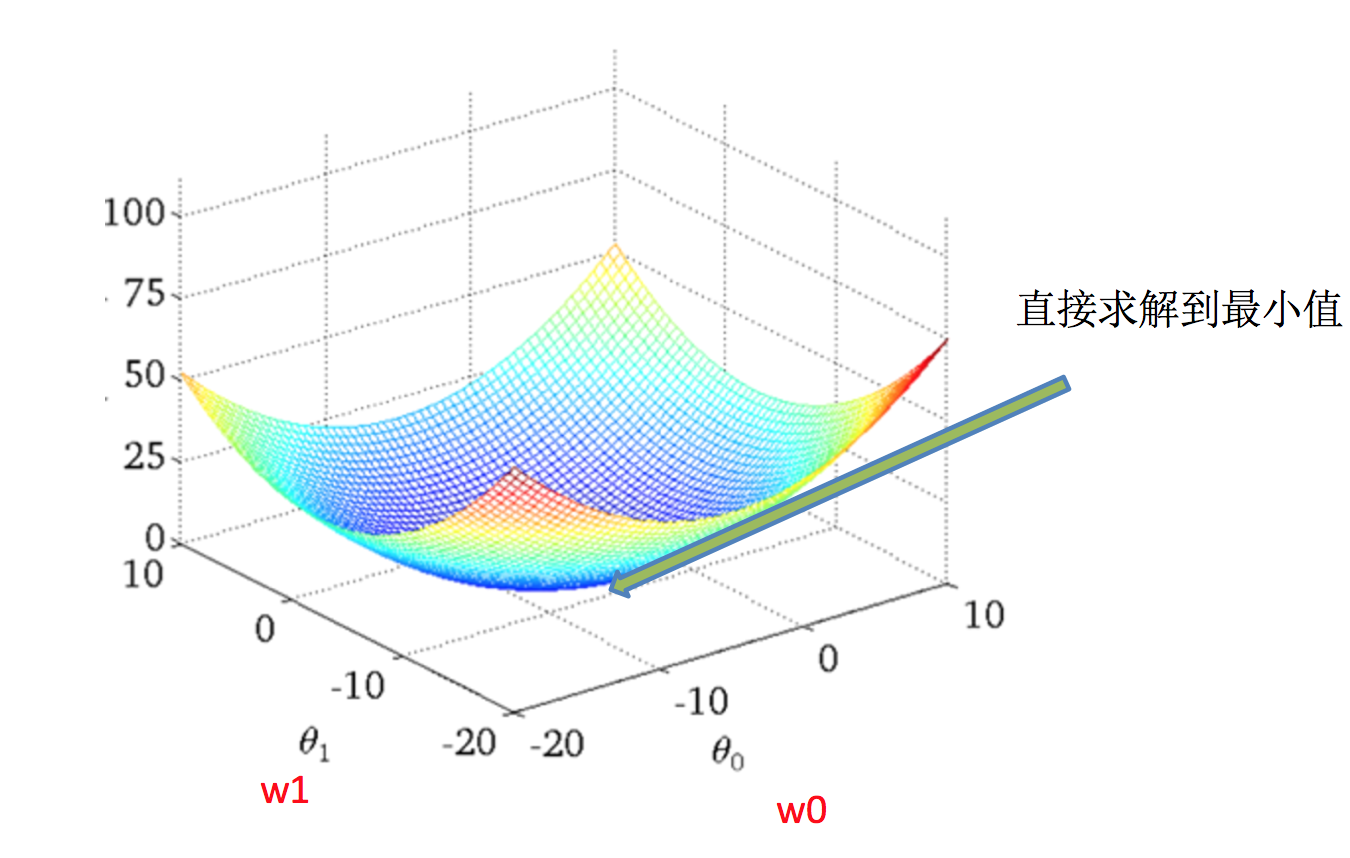
• 梯度下降(Gradient Descent)
• 

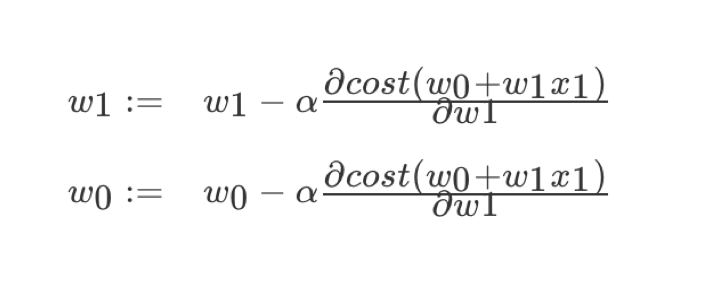
理解：α为学习速率，需要手动指定（超参数），α旁边的整体表示方向

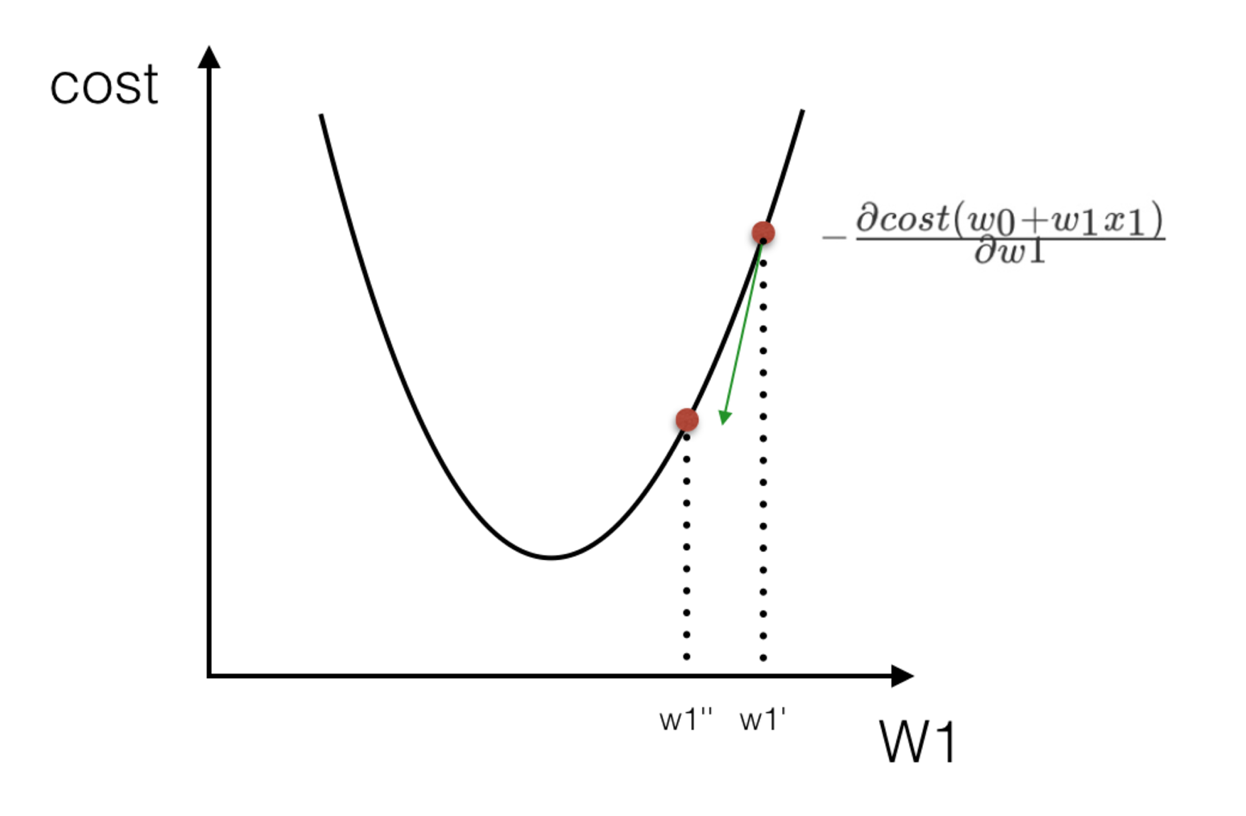
沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新W值

使用：面对训练数据规模十分庞大的任务 ，能够找到较好的结果

我们通过两个图更好理解梯度下降的过程

线性回归API

• sklearn.linear_model.LinearRegression(fit_intercept=True)
  • 通过正规方程优化
  • fit_intercept：是否计算偏置
  • LinearRegression.coef_：回归系数
  • LinearRegression.intercept_：偏置
• sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
  • SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
  • loss:损失类型
    • loss=”squared_loss”: 普通最小二乘法
  • fit_intercept：是否计算偏置
  • learning_rate : string, optional
    • 学习率填充
    • 'constant': eta = eta0
    • 'optimal': eta = 1.0 / (alpha * (t + t0)) [default]
    • 'invscaling': eta = eta0 / pow(t, power_t)
      • power_t=0.25:存在父类当中
    • 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
  • SGDRegressor.coef_：回归系数
  • SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API， 可以根据选择使用

波士顿房价预测

• 数据介绍

 

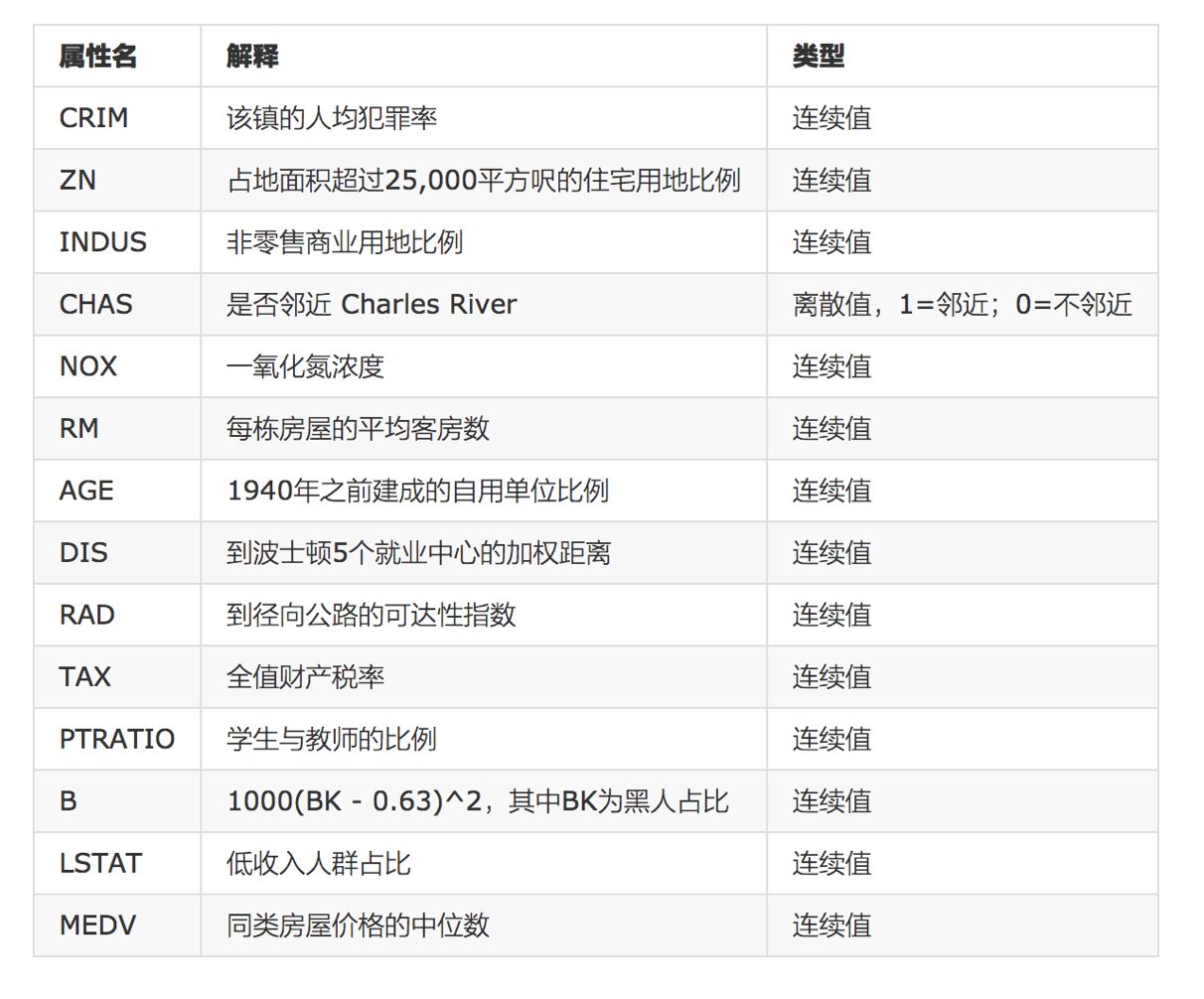
分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。同时我们对目标值也需要做标准化处理。

• 数据分割与标准化处理
• 回归预测
• 线性回归的算法效果评估

回归性能评估

均方误差(Mean Squared Error)MSE)评价机制：

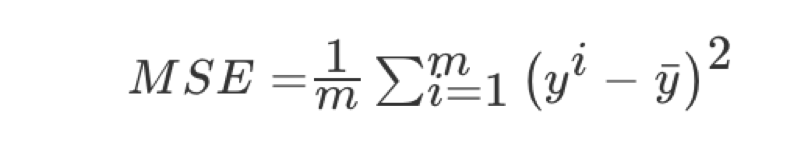
注：y^i为预测值，¯y为真实值

 sklearn.metrics.mean_squared_error(y_true, y_pred)

• 均方误差回归损失
• y_true:真实值
• y_pred:预测值
• return:浮点数结果

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.externals import joblib

def linear1():
    """
    正规方程的优化方法对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5）得出模型
    print("正规方程-权重系数为：
", estimator.coef_)
    print("正规方程-偏置为：
", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：
", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("正规方程-均方误差为：
", error)

    return None


def linear2():
    """
    梯度下降的优化方法对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()
    print("特征数量：
", boston.data.shape)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000, penalty="l1")
    estimator.fit(x_train, y_train)

    # 5）得出模型
    print("梯度下降-权重系数为：
", estimator.coef_)
    print("梯度下降-偏置为：
", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：
", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("梯度下降-均方误差为：
", error)

    return None
if __name__ == "__main__":
    # 代码1：正规方程的优化方法对波士顿房价进行预测
    linear1()
    # 代码2：梯度下降的优化方法对波士顿房价进行预测
    linear2()

结果：

正规方程-权重系数为：
 [-0.63330277  1.14524456 -0.05645213  0.74282329 -1.95823403  2.70614818
 -0.07544614 -3.29771933  2.49437742 -1.85578218 -1.7518438   0.8816005
 -3.92011059]
正规方程-偏置为：
 22.62137203166228
预测房价：
 [28.23494214 31.51307591 21.11158648 32.66626323 20.00183117 19.06699551
 21.0961119  19.61374904 19.61770489 32.88592905 20.9786404  27.52841267
 15.54828312 19.78740662 36.89507874 18.81564352  9.34846191 18.49591496
 30.67162831 24.30515001 19.06869647 34.10872969 29.82133504 17.52652164
 34.90809099 26.5518049  34.71029597 27.42733357 19.096319   14.92856162
 30.86006302 15.8783044  37.1757242   7.80943257 16.23745554 17.17366271
  7.46619503 20.00428873 40.58796715 28.93648294 25.25640752 17.73215197
 38.74782311  6.87753104 21.79892653 25.2879307  20.43140241 20.47297067
 17.25472052 26.14086662  8.47995047 27.51138229 30.58418801 16.57906517
  9.35431527 35.54126306 32.29698317 21.81396457 17.60000884 22.07940501
 23.49673392 24.10792657 20.13898247 38.52731389 24.58425972 19.7678374
 13.90105731  6.77759905 42.04821253 21.92454718 16.8868124  22.58439325
 40.75850574 21.40493055 36.89550591 27.19933607 20.98475235 20.35089273
 25.35827725 22.19234062 31.13660054 20.39576992 23.99395511 31.54664956
 26.74584297 20.89907127 29.08389387 21.98344006 26.29122253 20.1757307
 25.49308523 24.08473351 19.89049624 16.50220723 15.21335458 18.38992582
 24.83578855 16.59840245 20.88232963 26.7138003  20.75135414 17.87670216
 24.2990126  23.37979066 21.6475525  36.8205059  15.86479489 21.42514368
 32.81282808 33.74331087 20.62139404 26.88700445 22.65319133 17.34888735
 21.67595777 21.65498295 27.66634446 25.05030923 23.74424639 14.65940118
 15.19817822  3.8188746  29.18611337 20.67170992 22.3295488  28.01966146
 28.59358258]
正规方程-均方误差为：
 20.630254348291196
特征数量：
 (506, 13)
梯度下降-权重系数为：
 [-0.54822073  1.4464675  -0.22154422  0.39773236 -2.17831164  2.58570593
 -0.02940976 -2.92775196  2.52165579 -1.9505169  -1.69912449  1.0781636
 -4.12852256]
梯度下降-偏置为：
 [22.50159081]
预测房价：
 [27.97352427 31.52340503 20.70036447 31.15886575 20.1498911  18.28543117
 20.7848885  20.21984956 20.01274913 32.10649772 20.69410057 27.23525328
 14.69917195 18.90176799 36.020544   18.63530452  7.63275311 18.6544128
 31.09308283 24.74005178 18.08396144 33.74855729 28.14322275 16.97637572
 34.89911836 26.61471854 36.35192005 28.63558818 18.0587059  15.84963895
 30.42532827 14.8199527  38.82756129  6.80581813 16.21541358 16.27563381
  6.56726007 19.56205898 39.8180483  29.76142841 25.61631634 16.62787834
 36.01756452  5.74352165 21.36338418 25.37124012 17.69365175 19.69198194
 15.74601758 25.19781403  7.08602575 28.16384523 29.27243781 15.5603172
  7.34660494 35.24684654 33.97022255 22.31310221 17.47900314 23.46066882
 23.59667041 24.32300644 20.5174874  39.13901308 24.97850472 18.66494108
 12.09342626  5.89898225 39.68279945 22.35877144 15.47619425 23.35593401
 40.38069229 22.4053138  36.60422831 27.13321938 22.81114392 19.57121962
 25.97766409 22.68842564 31.30966289 20.80935726 22.56170642 33.48255719
 26.41207511 20.26886403 29.088948   22.72527639 26.21551635 19.34640023
 27.35484442 22.36210056 18.78086691 16.34377993 13.22087959 17.61309029
 24.99376174 15.17514227 20.02213586 26.48785524 19.56648084 16.77300822
 23.66739732 23.25336033 20.94984984 36.2192629  16.07989762 21.85319257
 33.70299197 31.57787594 20.72454564 27.25534697 19.63151962 16.90673351
 22.13481485 23.96593272 29.8023986  27.52424559 23.70090731 13.7158367
 13.88030813  2.61748894 29.38375773 19.77336278 22.70491118 28.48245522
 27.87704294]
梯度下降-均方误差为：
 20.476433191431912

正规方程和梯度下降对比

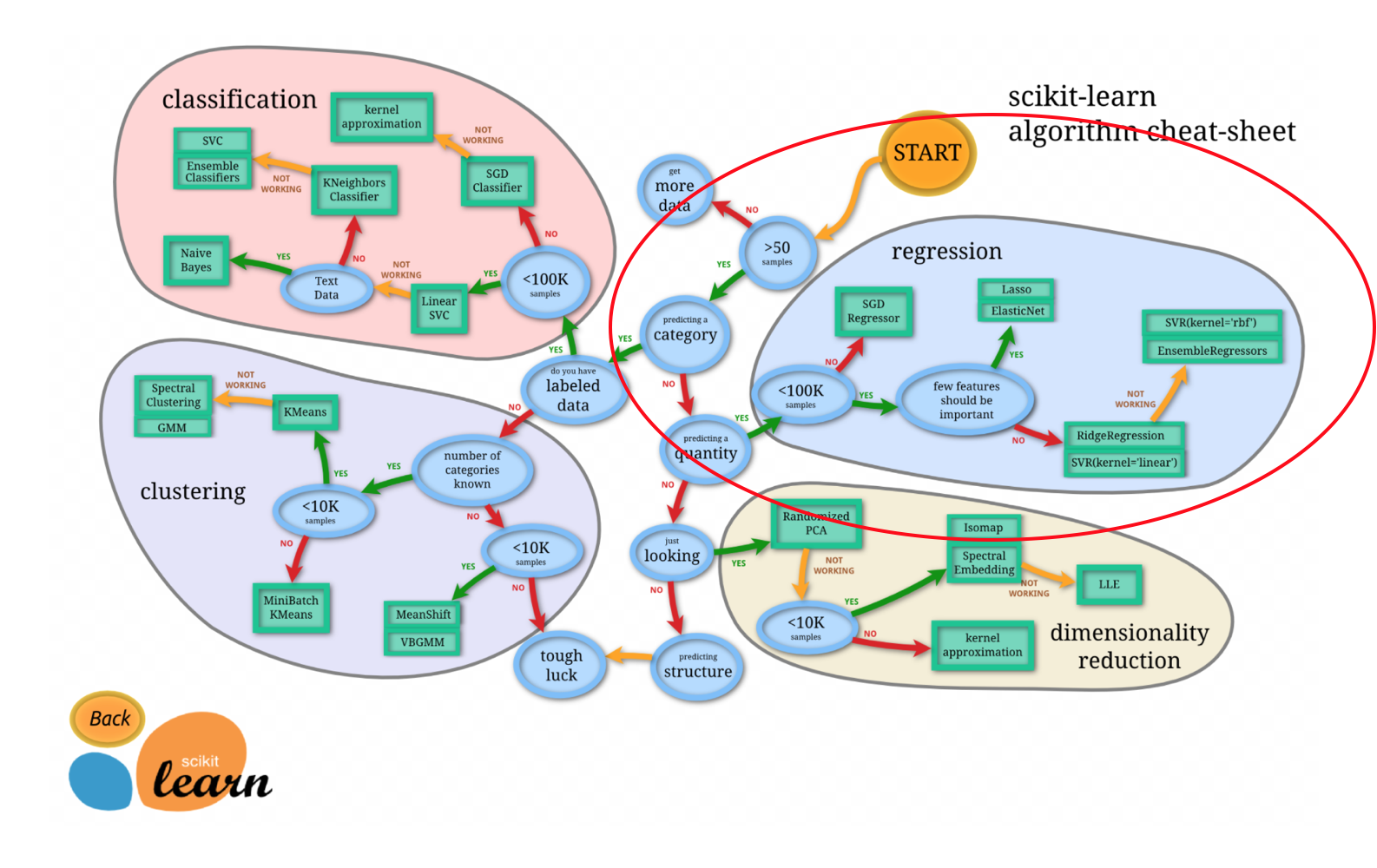
• 文字对比

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

• 选择：
  • 小规模数据：
    • LinearRegression(不能解决拟合问题)
    • 岭回归
  • 大规模数据：SGDRegressor

拓展-关于优化方法GD、SGD、SAG

GD

梯度下降(Gradient Descent)，原始的梯度下降法需要计算所有样本的值才能够得出梯度，计算量大，所以后面才有会一系列的改进。

SGD

随机梯度下降(Stochastic gradient descent)是一个优化方法。它在一次迭代时只考虑一个训练样本。

• SGD的优点是：
  • 高效
  • 容易实现
• SGD的缺点是：
  • SGD需要许多超参数：比如正则项参数、迭代数。
  • SGD对于特征标准化是敏感的。

SAG

随机平均梯度法(Stochasitc Average Gradient)，由于收敛的速度太慢，有人提出SAG等基于梯度下降的算法

欠拟合与过拟合

训练数据训练的很好啊，误差也不大，为什么在测试集上面有问题呢？

当算法在某个数据集当中出现这种情况，可能就出现了过拟合现象。

什么是过拟合与欠拟合

• 欠拟合

• 过拟合

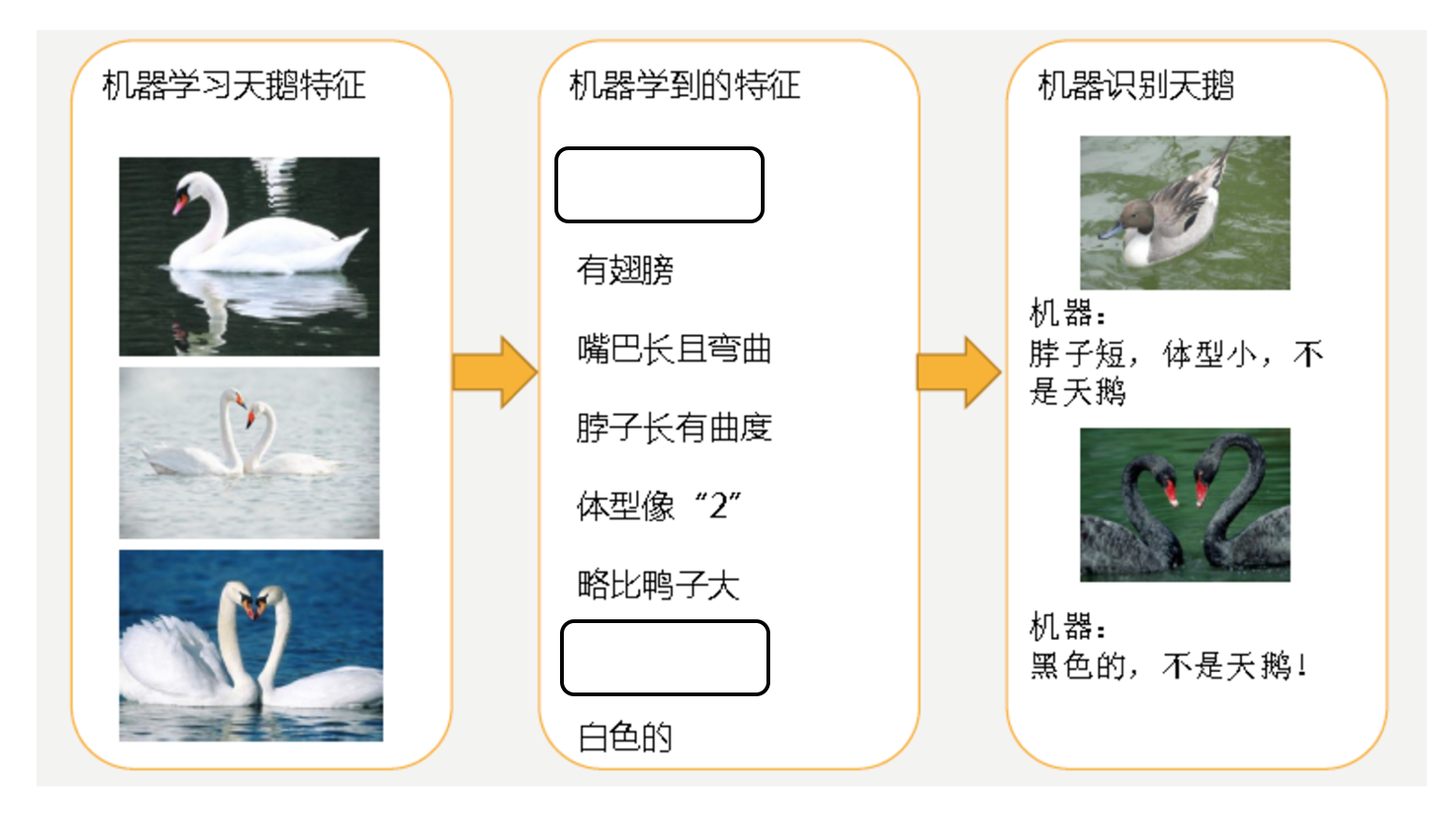
• 分析
  • 第一种情况：因为机器学习到的天鹅特征太少了，导致区分标准太粗糙，不能准确识别出天鹅。
  • 第二种情况：机器已经基本能区别天鹅和其他动物了。然后，很不巧已有的天鹅图片全是白天鹅的，于是机器经过学习后，会认为天鹅的羽毛都是白的，以后看到羽毛是黑的天鹅就会认为那不是天鹅。

定义

• 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
• 欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

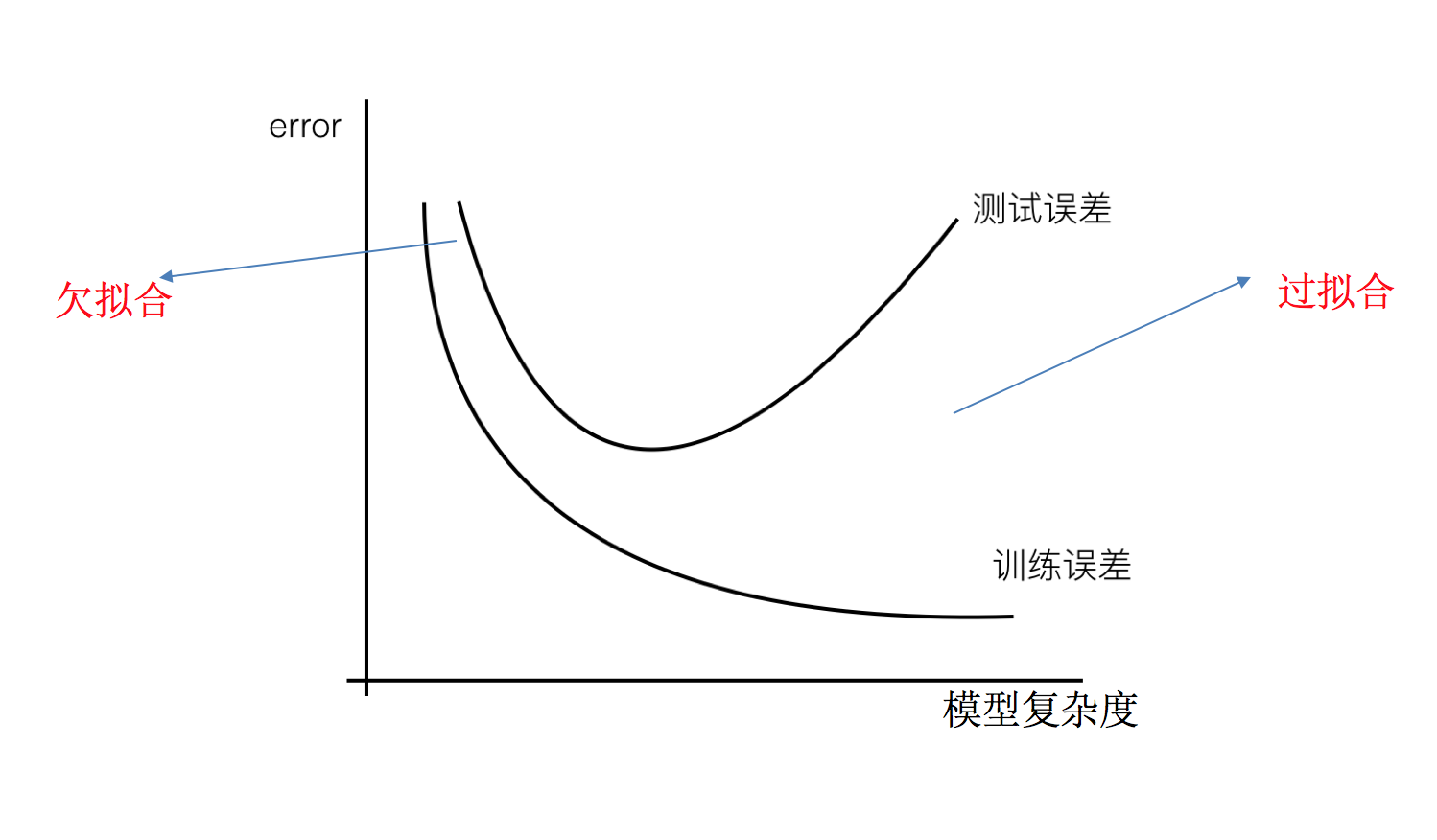
原因以及解决办法

• 欠拟合原因以及解决办法
  • 原因：学习到数据的特征过少
  • 解决办法：增加数据的特征数量
• 过拟合原因以及解决办法
  • 原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点
  • 解决办法：
    • 正则化

在这里针对回归，我们选择了正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括之前说的删除、合并一些特征

如何解决？

正则化类别

• L2正则化
  • 作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
  • 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
  • Ridge回归
• L1正则化
  • 作用：可以使得其中一些W的值直接为0，删除这个特征的影响
  • LASSO回归