算法复习-动态规划

终于到了著名的老大难问题——DP问题。

基本思想

在实际生活中，有一类问题的活动过程可以分成若干个阶段，而且在任一阶段后的行为依赖于该阶段的状态，与该阶段之前的过程是如何达到这种状态的方式无关。这类问题的解决是多阶段的决策过程。

20世纪50 年代，贝尔曼（Richard Bellman）等人提出了解决这类问题的“最优化原则”，指出多阶段过程的最优决策序列具有性质：

无论过程的初始状态和初始决策是什么，其余的决策都必须相对于初始决策所产生的状态构成一个最优决策序列。

这要求原问题计算模型的最优解需包含其（相干）子问题的一个最优解（称为最优子结构性质）。

动态规划算法就是采用最优化原则来建立递归关系式（关于求最优值的），在求解问题时有必要验证该递归关系式是否保持最优化原则。若不保持，则动态规划算法不适合求解该计算模型。在得到最优值的递归式之后，需要执行回溯以构造最优解。在使用动态规划算法自顶向下（Top-Down）求解时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次，动态规划算法正是利用了这种子问题重叠性质，对每一个子问题只计算一次，将其解保存在一个表格中，当再次要解此子问题时，只是简单地调用（用常数时间）一下已有的结果。

最优子结构性质和子问题重叠性质是计算模型采用动态规划算法求解的两个基本要素。

多段图问题

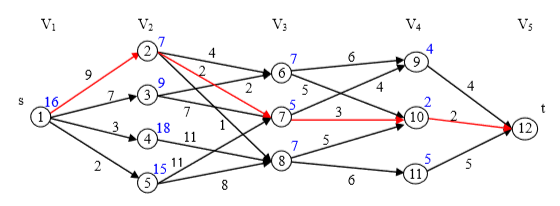
设(G=(V,E))是一个赋权有向图，其顶点集(V)被划分成(k(k>2))个不相交的子集(V_i: 1 le i le k)，其中，(V_1)和(V_k)分别只有一个顶点(s)(称为源)和一个顶点(t)(称为汇)，上图中所有的边((u,v))的始点和终点都在相邻的两个子集(V_i)和 (V_{i＋1})中，而且(u in Vi，v in V_{i＋1})。多段图问题是：求由(s)到(t)的最小成本路径（也叫最短路径）。

这里简单证明一下这个问题具有最优子结构：我们假设存在一条从源点到汇点的最短路径：

[s, v_2, v_3, v_4, ......, v_{k-1}, t ]

假设从(s)到(v_2)的决策是我们做出的初始决策。那么可以把(v_2)看做子问题的初始状态，那么这个问题变成寻找从(v_2)到(t)的一条最短路径，如果这个问题不具有最优子结构，那么从(v_2)到(t)则一定存在一条路径，比(v_2, v_3, v_4, ......, v_{k-1}, t)这条路径还短。那么(s, v_2, v_3, v_4, ......, v_{k-1}, t)就不是最短路径，这与我们的假设矛盾。所以这个问题具有最优子结构。

既然有最优子结构同时子问题重叠，那么就可以用动态规划算法。不难写出递推关系式：

[dp[i][j] = mathop {min }limits_{l in {V_{i + 1}},(j,l) in E} {c[j][l] + dp[i+1][l]} ]

其中(dp[i][j])表示在第(i)段中顶点(j)到汇点(t)的最短距离，这是一个从后向前的过程。

也可以从前向后，不过(dp)数组的意义要修改一下，这时(dp[i][j])表示源点(s)到第(i)段顶点(j)的最短距离，递推关系式为：

[dp[i][j] = mathop {min }limits_{l in {V_{i - 1}},(l,j) in E} { dp[i - 1][l] + c[l][j]} ]

进一步地，根据多段图的性质，一个顶点只能属于一个段，所以可以把(dp)数组压缩为1维数组，(dp[i])表示顶点(i)到源点或汇点的距离。

如果我们用邻接链表表示(G)，根据分析，得到算法的时间复杂度是(Theta(n+|E|))，因为我们要考虑(n)个节点，同时需要找出与各个节点相连的其他节点，就相当于在n次循环结束后要遍历完图中所有的边，同时找出最短路径的时间复杂度是(Theta(k) le n)，所以时间复杂度是(Theta(n+|E|))。如果用邻接矩阵表示，那么时间复杂度是(O(n^2))。

分析了这么多，代码也就呼之欲出了（这里以邻接矩阵存储图结构、且从后往前递推为例，(G[i][j]>0)表示节点(i,j)之间有链接且权值存储在这里）：

vector<int> multiGraph(vector<vector<int>>& G, int k)
{
    // 这里要求G中节点的编号是按照分段排列好的。
    // 例如：源点[0]，第一段[1,2,3]，第二段[4,5,6,7]，......， 第k段[n-3, n-2]，汇点[n-1]
    int n = G.size();
    vector<int> dp(n, INT_MAX);
    // next: 存储最短路径上当前节点的后继节点。
    vector<int> next(n, 0);
    dp[n-1] = 0;
    for(int j = n - 2 ; j >= 0 ; --j)
    {
        for(int r = j + 1 ; r < n ; r++)
        {
            if(G[j][r] > 0 && dp[j] > G[j][r] + dp[r])
            {
                dp[j] = G[j][r] + dp[r];
                next[j] = r;
            }
        }
    }
    // res：记录最短路径的节点顺序。
    vector<int> res(k, 0);
    res[0] = 0, res[k-1] = n-1;
    for(int j = 1 ; j < k - 1 ; ++j)
        res[j] = res[next[j-1]];
    return res;
}

矩阵连乘问题

给定(n)个数字矩阵(A_1，A_2，…，A_n)，其中(A_i)与(A_{i+1})是可乘的，(i=1,2,…,n-1). 求矩阵连乘(A_1A_2...A_n)的加括号方法，使得所用的数值乘法运算次数最少。

可见加括号的顺序不同会带来乘法次数的差异。对于(n)个矩阵的连乘积，令(P(n))表示前n个矩阵连乘积的加括号数，则有如下递归关系：

[P(n) = left{ egin{array}{l} 1,n = 1\ sumlimits_{k = 1}^{n - 1} {P(k)P(n - k),n ge 2} end{array} ight.]

可以算出(P(n)=C(n-1))，其中(C(n))表示卡特兰数。

[C(n) = frac{1}{{n + 1}}left( egin{array}{l} 2n\ n end{array} ight) = Omega ({4^n}/{n^{3/2}})]

所以，枚举所有(P(n))的情况是不现实的，我们考虑使用动态规划的做法解决这个问题。因为一个最优加括号方法的矩阵子链也必定采用了最优加括号方法，也就是说具有最优子结构。

那么我们可以直接采用递归的方法，令(m[i,j])表示计算矩阵链(A_{i,...,j})所需乘法次数的最小值。那么(m[i,j])可以写出如下的递推式：

[m[i,j] = left{ egin{array}{l} 0,i = j\ mathop {min }limits_{i le k < j} { m[i,k] + m[k + 1,j] + {p_{i - 1}}{p_k}{p_j}} ,i < j end{array} ight.]

可以看出，计算(m[i,j])需要([i,j])左侧和下侧的结果，也就是说需要知道跨度小于(j-i+1)的所有结果。因为我们需要得到最终的最优加括号计算次数和方法，所以用一个(s)表示加括号的位置，(s[i,j])表示在计算(A_i...A_j)的时候需要加括号的位置。

void printOptimalParens(vector<vector<int>>& s, int i, int j)
{
    if(i == j) 
    {
        printf("A%d", i);
        return;
    }
    printf("(");
    printOptimalParens(s, i, s[i][j]);
    printOptimalParens(s, s[i][j]+1, j);
    printf(")");
}

void matrixChainOrder(vector<int>& p)
{
    int n = p.size() - 1;
    vector<vector<int>> m(n+1, vector<int>(n+1, 0));
    vector<vector<int>> s(n, vector<int>(n+1, 0));
    for(int l = 2 ; l <= n ; ++l)
    {
        for(int i = 1 ; i <= n-l+1 ; i++)
        {
            int j = i + l - 1;
            m[i][j] = INT_MAX;
            for(int k = i ; k <= j - 1 ; k++)
            {
                int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if(q < m[i][j])
                {
                    m[i][j] = q;
                    s[i][j] = k;
                }
            }
        }
    }
    printOptimalParens(s, 1, n);
}
int main()
{
    vector<int> p = {30,35,15,5,10,20,25};
    matrixChainOrder(p);
    return 0;
}

执行过程如下：

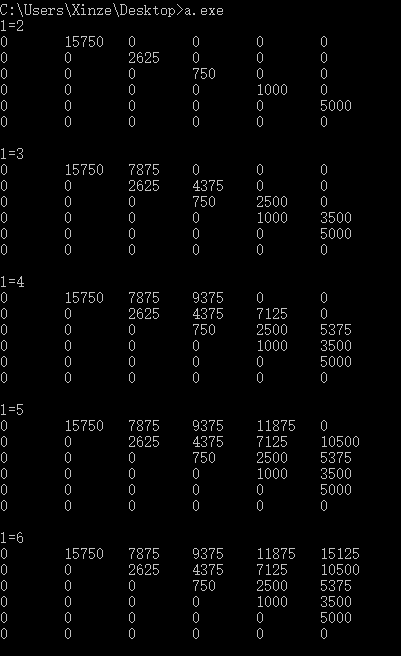
可见算法的复杂度是(O(n^3))。

0/1背包

0/1背包问题有很多种解法，动态规划问题是其中的一种解法。

问题可用下面的数学语言描述：

[max sumlimits_{i = 1}^n {{p_ix_i}} ,(sumlimits_{i = 1}^n {{w_i}{x_i} le c,{x_i} = 0,1)} ]

递推关系式为：

[m[i][W] = max(m[i-1][W], m[i-1][W-w[i]]+p[i]) ]

发现这个递推关系式可以用滚动数组优化，代码为：

int main()
{
    int N, V;
    cin >> N >> V;
    int w[MAX], p[MAX];
    for(int i = 0 ; i < N ; i++)
    {
        cin >> w[i] >> p[i];
    }
    int dp[MAX] = {0};
    int res[MAX][MAX] = {0};
    for(int j = 0 ; j < N ; j++)
    {
        for(int i = V ; i > 0 ; --i)
        {
            if(i - w[j] >= 0)
            {
                if(dp[i] < dp[i-w[j]] + p[j])
                {
                    dp[i] = dp[i-w[j]] + p[j];
                    res[j][i] = 1;
                }
                else res[j][i] = 0;
            }
        }
    }
    for(int j = N, i = V ; j >= 0 ; j--)
    {
        if(i > 0 && res[j][i] == 1)
        {
            printf("%d: %d %d
", j, w[j], p[j]);
            i -= w[j];
        }
    }
    printf("
");
    printf("%d", dp[V]);
    return 0;
}

注：课上讲的方法比这个的复杂度（(O(nV))）低，但是比较难理解。简单来说就是枚举所有的情况，之后去掉容量大但是价值低的点偶，去掉容量超出的点偶，最后得到最优解数值，之后通过每一步点偶的情况判断是否包含在最优解中。我觉得用组合的角度看更好理解，详见教材P120-121。

流水调度问题

我果然还是太菜了，还是直接看大佬的好一些QAQ，这里是一篇很详细的文章，感谢大佬。

这里强烈建议推一遍公式，感觉真的很爽！下面是流水调度问题的算法描述：

我们发现，这个算法其实就是在构造一个Johnson调度，不妨来验证一下，我们假设(AB)和(BA)中的元素已经按照算法要求排好序：

设(a_1, a_2 in AB)，有：

[a_1 < b_1, a_2 < b_2, 且a_1 le a_2 ]

[min(b_1, a_2) ge a_1,min(b_2, a_1)=a_1,所以min(b_1, a_2) ge min(b_2, a_1) ]

设(a_3, a_4 in BA)，有：

[a_3 ge b_3, a_4 ge b_4, 且b_3 ge b_4 ]

[min(b_3, a_4) ge b_4,min(b_4, a_3)=b_4,所以min(b_3, a_4) ge min(b_4, a_3) ]

一定存在一个(i)，使得(a_i in AB,a_{i+1} in BA)，有：

[a_i < b_i, a_{i+1} ge b_{i+1} ]

if (a_i ge a_{i+1}), then (min(b_i, a_{i+1})=a_{i+1},min(b_{i+1}, a_i)=b_{i+1})，所以满足Johnson不等式；
if (a_i < a_{i+1}) and (min(b_i, a_{i+1})=b_i), then if (min(b_{i+1}, a_i)=b_{i+1}), then (b_{i+1} ge a_i > b_i), 满足，else (min(b_{i+1}, a_i)=a_i), then (b_i>a_i) ,满足。
if (a_i < a_{i+1}) and (min(b_i, a_{i+1})=a_{i+1})，同理。

综上，算法得出的调度过程满足Johnson不等式，是一个Johnson调度，所以是最优调度。

算法时间复杂度是(O(nlogn))，因为大部分时间花费在排序过程中，空间复杂度是(O(n))。

最优二叉搜索树

这个问题没有上面那些问题那样直观。

我们可以认为(b_i)表示在二叉树中找到第(i)个节点的概率，直接看个例子吧：

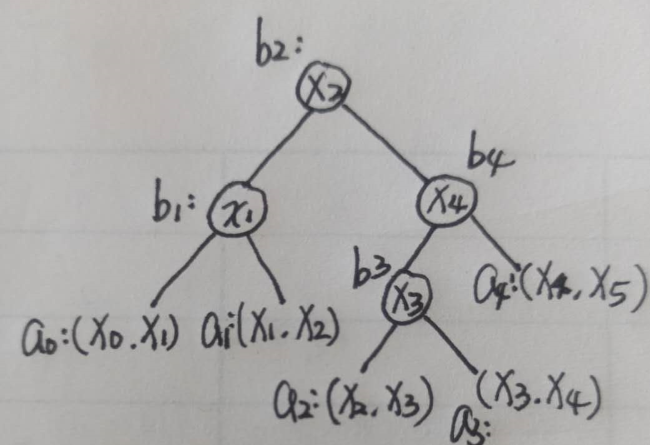
首先分析这个问题是否具有最优子结构，假设(T_{ij})是有序集({x_i,x_{i+1}, ..., x_j})关于存储概率分布({ overline {{a_{i - 1}}} ,overline {{b_i}} ,...,overline {{b_{j - 1}}} ,overline {{a_j}} })的一颗最优二叉搜索树，其平均路长记为(p_{ij}). (T_{ij})的根顶点存储的元素是(x_m), 其左子树(T_l)和右子树(T_r)的平均路长分别记为(p_l)和(p_r)。由于(T_l)和(T_r)中顶点深度是它们在(T_{ij})中的深度减1，有如下推导：

[{w_{ij}} = sumlimits_{k = i - 1}^j {{a_k}} + sumlimits_{k = i}^j {{b_k}} ]

所以：

实验验证：

#include<stdio.h>
#include<stdlib.h>
#include<limits.h>

const int N = 1010;
int root[N][N];
double e[N][N], w[N][N];

void printTree(int start, int end)
{
    if(start > end)
        return;
    int r = root[start][end];
    if(start <= r - 1)
        printf("k%d is the lchild of k%d.
", root[start][r-1], r);
    else
        printf("d%d is the lchild of k%d.
", r-1, r);
    printTree(start, r-1);
    if(r + 1 <= end)
        printf("k%d is the rchild of k%d.
", root[r+1][end], r);
    else
        printf("d%d is the rchild of k%d.
", end, r);
    printTree(r+1, end);
}

int main()
{
    freopen("optimalBST.in", "r", stdin);
    int n;
    scanf("%d", &n);
    double p[N] = {0}, q[N] = {0};
    for(int i = 1 ; i <= n ; i++) scanf("%lf", &p[i]);
    for(int i = 0 ; i <= n ; i++) scanf("%lf", &q[i]);
    
    for(int i = 1 ; i <= n + 1 ; i++)
    {
        e[i][i-1] = q[i-1];
        w[i][i-1] = q[i-1];
    }
    
    for(int l = 1 ; l <= n ; l ++)
    {
        for(int i = 1 ; i <= n - l + 1 ; i++)
        {
            int j = i + l - 1;
            e[i][j] = INT_MAX;
            w[i][j] = w[i][j-1] + p[j] + q[j];
            for(int r = i ; r <= j ; r++)
            {
                if(e[i][j] > e[i][r-1] + e[r+1][j] + w[i][j])
                {
                    e[i][j] = e[i][r-1] + e[r+1][j] + w[i][j];
                    root[i][j] = r;
                }
            }
        }
    }
    printf("mincost is %lf, k%d is root.

tree structure:
", e[1][n], root[1][n]);
    printTree(1, n);
    return 0;
}

算法的时间复杂度是(O(n^3))。