看了下面这篇文章后就恍然大悟了,不得不佩服解题方法的精妙之处。
http://blog.csdn.net/wh2124335/article/details/8739097
题目大意:
在第一象限中给出若干矩形(点范围1e5,矩形个数20000),现在给出一些询问(次数20000),每次询问给出一个整数t,问在(0,0)到(t,t)范围的矩形面积和。
解题思路:
考虑每次询问t,对于单一矩形的面积的计算方法~
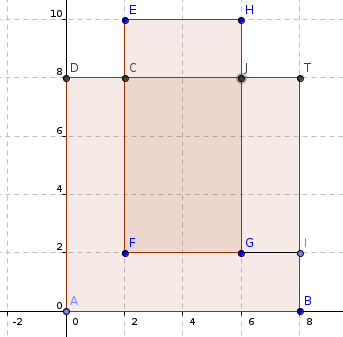
对于询问t。计算如图矩形所被包含的面积可以用矩形面积S[TCFI]-S[TJGI],而S[TCFI]=(t-Fx)*(t-Fy);S[TJGI]=(t-Gx)*(t-Gy)
换句话说就是用[T和矩形左下角的点形成的面积]减去[T和矩形右下角形成的矩形面积]就是这个矩形被包含的面积!
下面来看一个类似的情况:
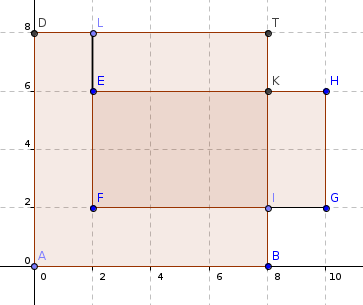
对于这次询问t。当前矩形被包涵的面积是S[TLFI]-S[TLEK]。即[T和矩形左下角点形成的面积]减去[T和矩形左上角点形成的矩形的面积]!
那么对于矩形被包含进(t,t)范围是什么情况呢?
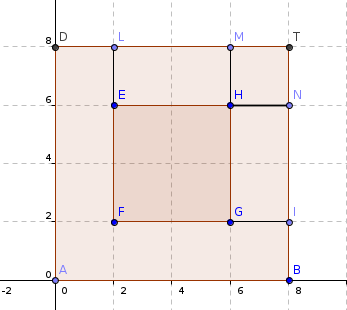
这时候的面积是EHGF的面积,但我们还想计算这个面积时和T有关。仿照前面的讨论,发现S[EHGF]不就是S[TLFI]-S[TLEN]-S[TMGI]+S[TMHN]么?
换句话描述,就是[T和矩形左下角点形成的矩形面积]减去[T和矩形左上角点形成的矩形面积]减去[T和矩形右下角点形成的矩形面积]加上[T和矩形右上角点形成的矩形面积]
那么我们得到了如下算法:
输入询问t
sum=0
遍历所有矩形的四个顶点
如果该顶点在(0,0)-(t,t)的范围内
如果当前顶点是它所在矩形的左上角或右下角的点那么sum+=[(t,t)和该点形成的矩形的面积]
否则sum-=[(t,t)和该点形成的矩形的面积]
返回sum
对于这题目的数据来说时间复杂度肯定是不够的,我们要想办法优化它。。。
观察我们计算[T和当前点形成的矩形面积]时的方法:
假设当前点坐标是(x,y)
那么S=(t-x)*(t-y)
我们可以将上式展开:S=t*t-t(x+y)+xy
我们可不可以将上式分成的三部分分别求和呢?答案是可以的!
那么我们可以将所有矩形左下角和右上角的点分到一组a(因为它们和T形成的矩形面积都是做“加”运算),把左上角和右下角的点分到一组b(因为它们和T形成的矩形面积都是做“减”运算)
那么结果可以写成sigma[a中在(t,t)范围内的点和T形成的矩形面积]-sigma[b在(t,t)范围内的点和T形成的矩形面积]
很容易想到,我们将a,b中的点分别按max(x,y)排序。然后正确的算法已经呼之欲出了!
对于每次询问t,我们二分找到它在a,b中的位置n,m(即max(x,y)恰好不超过t的最大的下标,a,b都是从1开始编号)
答案不就是
Sum(Sa)-Sum(Sb)
=sigma[t*t-t*(x+y)+xy](a中点)-sigma[t*t-t*(x+y)+xy](b中点)
=[sigma(t*t)-sigma(x+y)+sigma(xy)](a中点)-[sigma(t*t)-sigma(x+y)+sigma(xy)](b中点)
计算sigma(t*t)只要t*t乘个数(对于a是n,对于b是m)即可!
计算sigma(x+y)和sigma(xy)只要预处理一下即可!
现在算法如下:
检查所有矩形的四个顶点
如果是左下角或是右上角的点那么放到a的末尾
否则放到b的末尾
将a,b中的所有点按max(x,y)排序
定义suma,sumb表示a、b的点中下标1到下标i的所有点的x+y和
定义suma_mul,sumb_mul表示a、b的点中下标1到下标i的所有点的x*y和
循环 i=1 到 2*N
suma[i]=suma[i-1]+a[i].x+a[i].y
sumb[i]=sumb[i-1]+b[i].x+b[i].y
suma_mul[i]=suma_mul[i-1]+a[i].x*a[i].y
sumb_mul[i]=sumb_mul[i-1]+b[i].y*b[i].y
对于每次询问t
二分找到在a,b中max(x,y)恰好不超过t的下标n,m
输出答案(t*t*n-t*suma[n]+suma_mum[n])-(t*t*m-t*sumb[m]+sumb_mul[m])
另外:由于本题的询问范围是固定且是递增的,所以可以考虑在这里再次优化时间复杂度
// 以上内容为转载
代码如下:
#include <cstdio> #include <cstring> #include <cstdlib> #include <algorithm> using namespace std; typedef long long int64; int N, M; int64 saxay[20005*2], saxmy[20005*2]; int64 sbxay[20005*2], sbxmy[20005*2]; struct Node { int64 x, y; void set(int64 cx, int64 cy) { x = cx, y = cy; } bool operator < (const Node & t) const { return max(x, y) < max(t.x, t.y); // 按照被覆盖的时间排序 } bool operator < (int t) const { return max(x, y) < t; } }a[20005*2], b[20005*2]; void insert(int i) { int64 x1, y1, x2, y2; scanf("%I64d %I64d %I64d %I64d", &x1, &y1, &x2, &y2); a[i].set(x1, y1), a[i+1].set(x2, y2); b[i].set(x1, y2), b[i+1].set(x2, y1); } void deal() { for (int i = 1; i <= N*2; ++i) { saxay[i] = saxay[i-1] + a[i].x + a[i].y; saxmy[i] = saxmy[i-1] + a[i].x * a[i].y; sbxay[i] = sbxay[i-1] + b[i].x + b[i].y; sbxmy[i] = sbxmy[i-1] + b[i].x * b[i].y; } } int64 query(int ti) { int64 ret = 0; int pa = lower_bound(a+1, a+N*2+1, ti) - a - 1; int pb = lower_bound(b+1, b+N*2+1, ti) - b - 1; // pa, pb分别指向ti覆盖到了的点的位置 // printf("pa = %d, pb = %d\n", pa, pb); if (pa != 0) ret += 1LL*pa*ti*ti-ti*saxay[pa]+saxmy[pa]; if (pb != 0) ret -= 1LL*pb*ti*ti-ti*sbxay[pb]+sbxmy[pb]; return ret; } int main() { int T; scanf("%d", &T); while (T--) { scanf("%d", &N); for (int i = 0; i < N; ++i) { insert(i*2+1); } sort(a+1, a+1+2*N), sort(b+1, b+1+2*N); deal(); scanf("%d", &M); while (M--) { int ti; scanf("%d", &ti); printf("%I64d\n", query(ti)); } } return 0; }