POJ1392 Ouroboros Snake 欧拉回路

题意：对于一个长度为2^N的循环序列，从某一个位置开始依次取N个，这样就能够生成2^N个序列，现在要求输出一个最小的满足要求的循环序列。输出这个序列生成的第K个数字是多少？

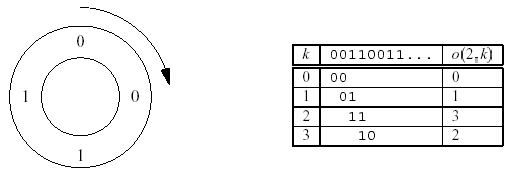
解法：套用Fleury算法，构边的时候保持从小到大的顺序即可。如果是生成N为序列的话，就考虑前N-1位构成的节点相互的连的边（例如三位数就可以这样构边 00 --> 01 --> 11那么这两条边就代表生成了001和011这两个数字），输出欧拉回路即可。

代码如下：

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = (1 << 15);
int n, k;
int stk[MAXN+5];
int path[MAXN+5];
int ans[MAXN+5];
int top;

struct Node { // f用来标志边是否被删除 
    int v, f;
    int next;
}e[MAXN*2+5]; // 每个节点最多生成两条边

int head[MAXN+5], idx; 

void insert(int a, int b) {
//    printf("a = %d, b = %d\n", a, b);
    e[idx].v = b, e[idx].f = 1;
    e[idx].next = head[a];
    head[a] = idx++;
}

void dfs(int x) {
    for (int i = head[x]; i != -1; i = e[i].next) {
        if (e[i].f) {
            stk[top++] = e[i].v;
            e[i].f = 0;
            dfs(e[i].v);
            break;
        }
    }    
}

void fleury(int ss) {
    int cnt = 0;
    top = 0;
    stk[top++] = ss;
    while (top > 0) {
        int brige = 1, v = stk[top-1];
        for (int i = head[v]; i != -1; i = e[i].next) {
            if (e[i].f) {
                brige = 0;
                break;
            }
        }
        if (!brige) {
            dfs(v);
        } else {
            --top; // 某联通子集中节点出栈
            path[cnt++] = v;
        }
    }
    for (int i = cnt-2, j = 0; i >= 0; --i, ++j) {
        ans[j] = (path[i+1] << 1) | (path[i] & 1);
    //    printf("path[%d] = %d\n", j, ans[j]);
    }
}

int main() {
    while (scanf("%d %d", &n, &k), n|k) {
        idx = 0; 
        memset(head, 0xff, sizeof (head));
        int lim = 1 << (n-1); // 只将前n-1位作为节点，后面一位放到边上，那么每条边都遍历一遍即使最后的结果 
    //    printf("lim = %d\n", lim);
        for (int i = 0; i < lim; ++i) {
            // 从每个节点有两个节点出去
            int t = i & ((lim-1)>>1);
            insert(i, t<<1|1);
            insert(i, t<<1); // 由于采用的前插入，因此较小的边后插入 
        }
        fleury(0);
        printf("%d\n", ans[k]);
    }
    return 0;
}