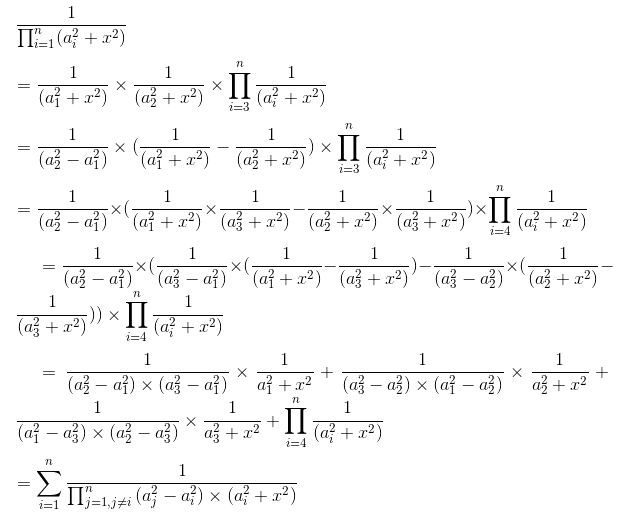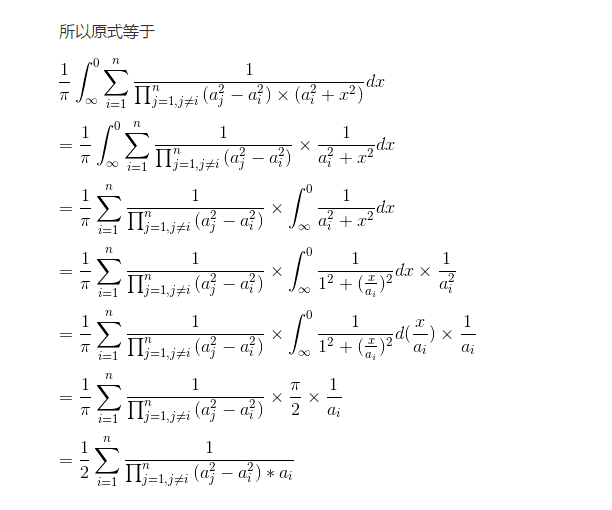A.Equivalent Prefixes
•题意
有两个数组a,b，现给一个定义，等价：
在区间[L,R]上的任意一个区间内，ai,bi最小值的位置相等，则称这两个数组是等价的
给你两个数组a,b，求a,b存在[1,R]是等价的最大的R
•思路
利用单调栈，求出每个ai,bi是最小值的左区间
当左区间不相同时，即可得到答案
•栗子
a数组 3 1 5 2 4
左区间 1 1 3 3 5
b数组 5 2 4 3 1
左区间 1 1 3 3 1
即可得到 R=4
•代码
View Code
B.Integration
•题意
解
对(109+7)取模的值
•思路
裂项相消，利用
参考这位大佬
把1/2乘进去得
然后利用费马小定理
(p/q)%mod≡p*q-1%mod
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const ll mod=1e9+7; 5 const int maxn=1e3+5; 6 ll a[maxn],b[maxn]; 7 int n; 8 9 ll quickMod(ll x,ll y) 10 { 11 ll res=1; 12 x=x%mod; 13 while(y) 14 { 15 if(y&1) 16 res=(res*x)%mod; 17 x=(x*x)%mod; 18 y>>=1; 19 } 20 return res; 21 } 22 23 int main() 24 { 25 while(scanf("%d",&n)!=EOF) 26 { 27 for(int i=1;i<=n;i++) 28 { 29 cin>>a[i]; 30 b[i]=(a[i]*a[i])%mod; 31 } 32 ll ans=0; 33 for(int i=1;i<=n;i++) 34 { 35 ll mul=a[i]*2; 36 for(int j=1;j<=n;j++) 37 { 38 if(j!=i) 39 mul=(mul*(b[j]-b[i]+mod)%mod)%mod; 40 } 41 mul=quickMod(mul,mod-2); 42 ans=(ans+mul)%mod; 43 } 44 cout<<ans<<endl; 45 } 46 return 0; 47 }
C.Euclidean Distance
•题意
给定一个N维坐标系的点A（a1/m,a2/m,a3/m,...,an/m），
寻找一个点P(p1,p2,p3,...,pn)满足p点的各坐标之和为1，且p1,p2,p3,...,pn > 0
使得A点到P点的欧几里得距离最小，
其中A与P之间的欧几里得距离即为∑n i=1(ai/m−pi)，
求这个最小的欧几里得距离，若为分数则用分数形式表示。
•思路
官方题解用拉格朗日乘子法做的，但是我不会(o(╥﹏╥)o
翻到这位大佬的博客，数形结合太形象了_(:з」∠)_
对于每个数 我们先不看分母，后来直接除分母就阔以
我们要使得减去pi后的ai平方和最小，那么是ai中较大的数减小的收益一定比使较小的数变小的收益大
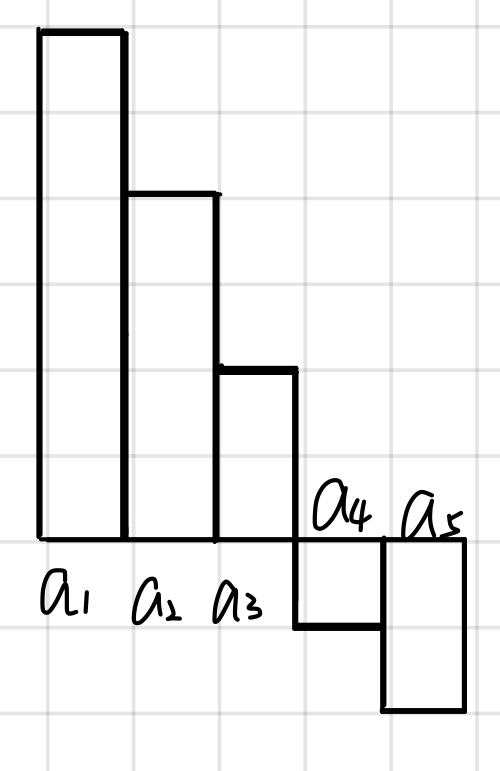
对于所有的a[i]，按从大到小排序，
来看下排序后的图
接下来我们需要确定P的坐标，也就是将 -m（因为在欧几里得距离中A和P的坐标是直接相减关系）分配到这个图
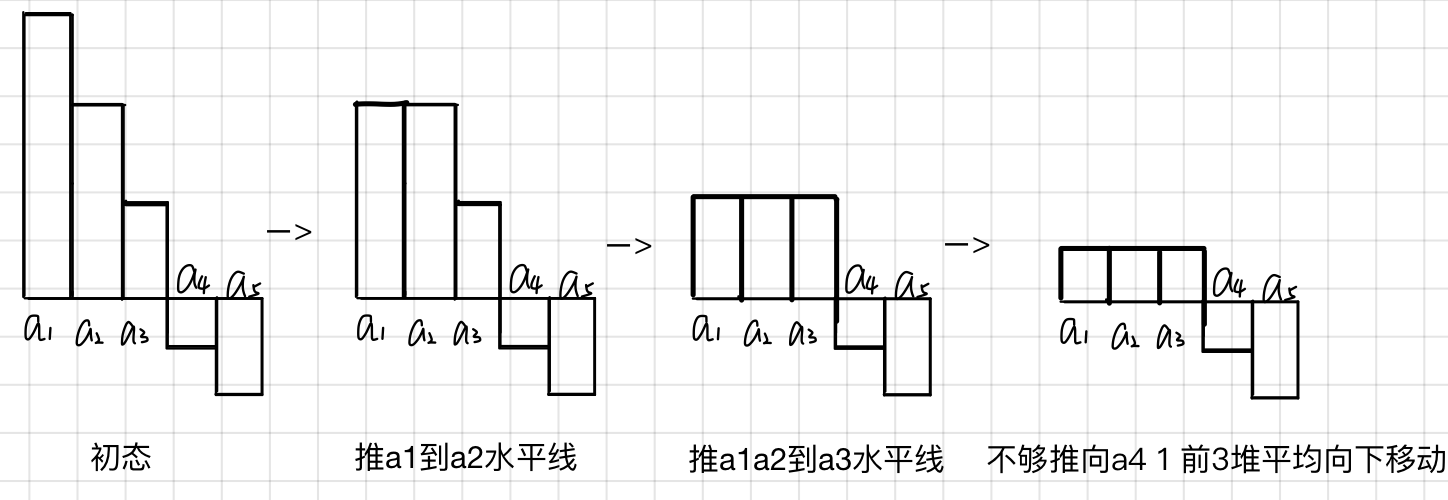
如何分配m呢？依次把最高堆的推向比较低的堆，直到不够再向下一堆(pos+1)的水平线推进为止，我们将m中未分配完称为rest
这时候未分配的rest再平均分配到所推进的前pos堆里去，也就是把这pos堆再往下推进rest/pos个单位
如图
关于分子分母处理看代码中的注释
•代码
View Code1 、#include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int maxn=1e4+5; 5 int a[maxn]; 6 int main() 7 { 8 int n,m; 9 while(~scanf("%d%d",&n,&m)) 10 { 11 for(int i=1;i<=n;i++) 12 cin>>a[i]; 13 sort(a+1,a+1+n,greater<int>()); 14 ll rest=m; //p[i]的总分配价值是 1 ,因为 ∑pi=m,也就是 m/m 15 int pos=1; //pos 标记能够分配p[i] 到第 pos 个 16 while(pos<n) 17 { 18 if(rest<(a[pos]-a[pos+1])*pos)//如果不能继续向下一水平线推 19 break; 20 rest-=(a[pos]-a[pos+1])*pos; 21 pos++; 22 } 23 24 //直到不能再往下一个堆(pos+1)的水平线推， 25 //那么剩余的可以再让前pos堆水平下推rest/pos个单位 26 //最终前pos堆的值 都是a[pos]-rest/pos, 27 //然后分子分母同乘pos,分子变为(a[pos]*pos-rest) 28 //平方后分子为(a[pos]*pos-rest)²，分母为(m*pos)² 29 //因为一共有pos堆分配到的，所以∑的结果分子为pos倍的 30 ll ansa=(a[pos]*pos-rest)*(a[pos]*pos-rest)*pos; 31 for(int i=pos+1;i<=n;i++) //分配不到的 a[i]，直接加上 32 ansa+=a[i]*a[i]*pos*pos; //因为分子乘了pos倍,记得平方 33 34 ll ansb=m*m*pos*pos; //分母(m*pos)² 35 ll gcd=__gcd(ansa,ansb); //求gcd 约分 36 if(gcd%ansb==0) 37 cout<<(ansa/ansb)<<endl; 38 else 39 cout<<ansa/gcd<<"/"<<ansb/gcd<<endl; 40 } 41 }
E.ABBA
•题意
有一个2(n+m)的序列，其中包括n各AB子序列，m个BA子序列
问这个序列有多少种情况,对109+7取模
•思路
定义dp[i][j]为有i个A,j个B的方案数
所以转移方程为
dp[i+1][j]=dp[i+1][j]+dp[i][j]
dp[i][j+1]=dp[i][j+1]+dp[i][j]
那怎么才能保证有n个AB呢？
前面的A的个数i比B的个数j多n的话，至少会形成n个AB
同理前面的B的个数j比A的个数多m的话，至少会形成m个BA
参考此处
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const ll mod=1e9+7; 5 const int maxn=1e3+5; 6 ll dp[maxn*2][maxn*2]; 7 int n,m; 8 int main() 9 { 10 while(~scanf("%d%d",&n,&m)) 11 { 12 for(int i=0;i<=n+m;i++) 13 for(int j=0;j<=n+m;j++) 14 dp[i][j]=0; 15 dp[0][0]=1; 16 17 for(int i=0;i<=n+m;i++) 18 { 19 for(int j=0;j<=n+m;j++) 20 { 21 if(i-j<n)//此时小于n个AB 22 dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod; 23 if(j-i<m)//此时小于m个BA 24 dp[i][j+1]=(dp[i][j+1]+dp[i][j])%mod; 25 } 26 } 27 cout<<dp[n+m][n+m]<<endl; 28 } 29 }
F.Random Point in Triangle
•题意
给定三个顶点的坐标形成一个三角形(也可能不能构成)
存在一点P使得Sp=max{SPAB,SPBC,SPCA}
求36*(Sp的数学期望)
•思路
正解证明到现在也不会，等到会了再来补上，结论是22倍的面积
以下是非正解
纯暴力模拟找规律来着，
当SPAB=SPBC=SPCA时，P为三角形的重心
就假设一个很大的三角形，先求出面积，然后求出重心，再让去移动整数点，相当于模拟P点在上移。一直上移到顶点处，算一下是多少倍的面积因为给的坐标是整数，输出答案也是整数，就很容易往面积的偶数倍上去想(因为奇数倍可能不是整数多测几组数据，然后多wa几发就出来了...所以就有了上面的非正解...（大雾
•代码
暴力模拟的代码
View Code#include<bits/stdc++.h> using namespace std; double gets(int x1,int x2,int x3,int yl,int y2,int y3) { return abs(((x2-x1)*(y3-yl)-(x3-x1)*(y2-yl))); } int main() { int x1,x2,x3,yl,y2,y3; cin>>x1>>yl>>x2>>y2>>x3>>y3; int s=gets(x1,x2,x3,yl,y2,y3); cout<<"总面积："<<s<<" 1/3面积："<<1.0*s/3<<endl; double py=1.0*s/6/(x2-x3); cout<<"重心Py:"<<py<<endl; int tots=0; int num=0; for(int i=0;py<=y3;i++) { py+=1; num++; int ss=gets(x1,x2,(x1+x2)/2,yl,y2,py); tots+=ss; cout<<"上移"<<i<<"个：S="<<ss<<" 面积和："<<tots<<endl; } double p=1.0*tots/(1.0*num)/(1.0*s); cout<<p<<endl; cout<<"倍数："<<p*36<<endl; }AC代码
View Code#include<bits/stdc++.h> using namespace std; #define ll long long ll x1,yl,x2,y2,x3,y3; ll s; int main() { while(cin>>x1) { cin>>yl>>x2>>y2>>x3>>y3; s=((x2-x1)*(y3-yl)-(x3-x1)*(y2-yl)); cout<<abs(11*s)<<endl; } }
H.XOR（线性基）
•参考资料
[1]:【2019牛客多校第一场】XOR
•题意
有一个集合 S，里边有 n 个正整数（$a_1,a_2,cdots ,a_n$）；
对于 S 的某子集 s'，如果 s' 中所有元素的异或和为 0，就将 |s'| 加入到答案中；
求解所有的异或为 0 的子集的元素个数之和（$ans=sum |s'|$）；
注意，集合 ${2,2}$ 的可构成两个元素为 2 的子集 ${2_1},{2_2}$；
也就是说子集是否相同和下标有关而与子集的元素是否相同无关；
•思路
把求每个异或和为0的子集长度和转化为求每个$a_{i}$异或和为0的贡献
为什么可以这样转化呢？
例如 在所有异或和为0的子集里，$x$个有$a_{1}$,$y$个有$a_{2},...$
那么，$a_{1}$的贡献为$x$,$a_{2}$的贡献为$y,...$
如何算贡献呢？可以根据基底！分为在基底中的数和不在基底中的数
①不在基底中的数 $cnt dot 2^{cnt-1}$种
不在基底中的数，为什么不在基底中呢？因为加入后就线性相关，从而会产生0
得到所有不在基底中的数$cnt$,从这$cnt$个数中拿出$1$与在基底中的组合有$cnt$中
其他$cnt-1$个不在基底中的数，加入组合和不加入组合有$2^{cnt-1}$种，所有此种情况有$cnt dot 2^{cnt-1}$种
②在基底中的数
对于在基底中的数$a_{i}$，可能可以用其他数来代替，也可能不能被代替
把除$a_{i}$以外的所有数组成基底 (假设有$y$个对基底没有作用)
①不能被代替
也就是$a_{i}$与这个基底线性无关，可以插入到这个基底中，此时不能形成0
②可以被代替
也就是$a_{i}$与这个基底线性有关，不可以插入到这个基底中，此时可以形成0
那可以形成多少也就是贡献是多少呢？$2^{y}$
因为此时$a_{i}$和基底可以形成一个0，还有$y$个数加入组合和不加入组合形成$2^{y}$种
那$y$如何计算？可以得到所有不在基底中的数$cnt$，其中包含$a_{i}$,所以$y=cnt-1$
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mem(a,b) memset(a,b,sizeof(a)) 4 #define ll long long 5 const int maxn=1e5+50; 6 const int MOD=1e9+7; 7 8 int n; 9 ll a[maxn]; 10 ll base[70]; 11 ll L[maxn][70];///L[i]:前i个数（1~i）构成的基底 12 ll R[maxn][70];///R[i]:后n-i+1个数（i~n）构成的基底 13 bool vis[maxn];///vis[i]:判断a[i]是否在这n个数构成的基底中 14 15 bool Insert(ll x) 16 { 17 for(int i=60;i >= 0;--i) 18 { 19 if(x>>i&1) 20 { 21 if(!base[i]) 22 { 23 base[i]=x; 24 return true; 25 } 26 x ^= base[i]; 27 } 28 } 29 return false; 30 } 31 ll qPow(ll a,ll b,ll mod) 32 { 33 ll ans=1; 34 a %= mod; 35 while(b) 36 { 37 if(b&1) 38 ans=ans*a%mod; 39 a=a*a%mod; 40 b >>= 1; 41 } 42 return ans; 43 } 44 ll Solve() 45 { 46 mem(base,0); 47 for(int i=1;i <= n;++i) 48 { 49 vis[i]=Insert(a[i]); 50 memcpy(L[i],base,sizeof(base)); 51 } 52 53 mem(base,0); 54 mem(R[n+1],0); 55 for(int i=n;i >= 1;--i) 56 { 57 Insert(a[i]); 58 memcpy(R[i],base,sizeof(base)); 59 } 60 61 int cnt=n; 62 for(int i=0;i <= 60;++i) 63 if(base[i]) 64 cnt--; 65 ///计算出不在基底中的数对答案的贡献 66 ll ans=cnt*qPow(2,cnt-1,MOD); 67 68 for(int i=1;i <= n;++i) 69 { 70 if(!vis[i]) 71 continue; 72 73 ///base:除a[i]外的其他n-1个数构成的基底 74 memcpy(base,L[i-1],sizeof(L[i-1])); 75 for(int j=0;j <= 60;++j) 76 if(R[i+1][j]) 77 Insert(R[i+1][j]); 78 79 if(Insert(a[i]))///判断a[i]是否还可插入 80 continue; 81 82 cnt=n; 83 for(int j=0;j <= 60;++j) 84 if(base[j]) 85 cnt--; 86 ///a[i]对答案的贡献 87 ans += qPow(2,cnt-1,MOD); 88 ans %= MOD; 89 } 90 return ans; 91 } 92 int main() 93 { 94 while(~scanf("%d",&n)) 95 { 96 for(int i=1;i <= n;++i) 97 scanf("%lld",a+i); 98 99 printf("%lld ",Solve()%MOD); 100 } 101 return 0; 102 }