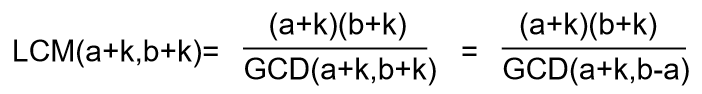•题意
给出两个正整数 a,b;
求解 k ,使得 LCM(a+k,b+k) 最小,如果有多个 k 使得 LCM() 最小,输出最小的k;
•思路
时隔很久,又重新做这个题
温故果然可以知新❤
重要知识点
GCD(a,b)=GCD(a,b-a)=GCD(b,b-a) (b>a)
证明:
设GCD(a,b)=c
则a%c=0,b%c=0,(b-a)%c=0
所以GCD(a,b-a)=c
得GCD(a,b)=GCD(a,b-a)
gcd(a+k,b-a)肯定是(b-a)的因子
所以gcd(a+k,b+k)是(b-a)的因子,所以我们就枚举(b-a)的因子(把因子称为i)
使得 (a+k)为i的倍数
解出k,再判断lcm是否符合最小
注意这里枚举的i只是(a+k)和(b+k)的公约数,不一定是最大公约数gcd
两者的公约数得到的是公倍数 公倍数=a*b/公约数
如果是最大公约数的话两者的公倍数一定是最小,
这里是没有甄别是否是最大公约数而是简单的得到公约数,然后得到的是公倍数
在所有的公倍数中,最小公倍数是最小的
所以并不影响解最小公倍数的答案
例如:
12 30
12 30
公约数i=1 k=1 a+k=13 b+k=31 公倍数=403
公约数i=2 k=2 a+k=14 b+k=32 公倍数=224
公约数i=3 k=3 a+k=15 b+k=33 公倍数=165
公约数i=6 k=6 a+k=18 b+k=36 公倍数=108
公约数i=9 k=6 a+k=18 b+k=36 公倍数=72
公约数i=18 k=6 a+k=18 b+k=36 公倍数=36最小公约数36,此时k=6
另外一个思路可以求最大公约数 然后求最小公倍数,看HHHyacinth的博客
•代码
 View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 ll a,b; 5 ll ans,lcm=0x3f3f3f3f3f3f3f3f; 6 int main() 7 { 8 cin>>a>>b; 9 ll d=abs(a-b); 10 for(ll i=1;i*i<=d;i++) 11 { 12 if(d%i==0)//枚举b-a的因数i 13 { 14 ll k=(i-a%i)%i;//把a凑成i的倍数需要+k 15 ll t=(a+k)*(b+k)/i;// a*b/i得公倍数 16 if(t<lcm) 17 { 18 lcm=t; 19 ans=k; 20 } 21 22 ll ii=d/i; 23 k=(ii-a%ii)%ii; 24 t=(a+k)*(b+k)/ii; 25 if(t<lcm) 26 { 27 lcm=t; 28 ans=k; 29 } 30 } 31 } 32 cout<<ans<<endl; 33 }
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 ll a,b; 5 ll ans,lcm=0x3f3f3f3f3f3f3f3f; 6 int main() 7 { 8 cin>>a>>b; 9 ll d=abs(a-b); 10 for(ll i=1;i*i<=d;i++) 11 { 12 if(d%i==0)//枚举b-a的因数i 13 { 14 ll k=(i-a%i)%i;//把a凑成i的倍数需要+k 15 ll t=(a+k)*(b+k)/i;// a*b/i得公倍数 16 if(t<lcm) 17 { 18 lcm=t; 19 ans=k; 20 } 21 22 ll ii=d/i; 23 k=(ii-a%ii)%ii; 24 t=(a+k)*(b+k)/ii; 25 if(t<lcm) 26 { 27 lcm=t; 28 ans=k; 29 } 30 } 31 } 32 cout<<ans<<endl; 33 }