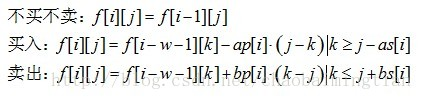Description
最近lxhgww又迷上了投资股票,通过一段时间的观察和学习,他总结出了股票行情的一些规律。 通过一段时间的观察,lxhgww预测到了未来T天内某只股票的走势,第i天的股票买入价为每股APi,第i天的股票卖出价为每股BPi(数据保证对于每个i,都有APi>=BPi),但是每天不能无限制地交易,于是股票交易所规定第i天的一次买入至多只能购买ASi股,一次卖出至多只能卖出BSi股。 另外,股票交易所还制定了两个规定。为了避免大家疯狂交易,股票交易所规定在两次交易(某一天的买入或者卖出均算是一次交易)之间,至少要间隔W天,也就是说如果在第i天发生了交易,那么从第i+1天到第i+W天,均不能发生交易。同时,为了避免垄断,股票交易所还规定在任何时间,一个人的手里的股票数不能超过MaxP。 在第1天之前,lxhgww手里有一大笔钱(可以认为钱的数目无限),但是没有任何股票,当然,T天以后,lxhgww想要赚到最多的钱,聪明的程序员们,你们能帮助他吗?
Input
输入数据第一行包括3个整数,分别是T,MaxP,W。 接下来T行,第i行代表第i-1天的股票走势,每行4个整数,分别表示APi,BPi,ASi,BSi。
Output
输出数据为一行,包括1个数字,表示lxhgww能赚到的最多的钱数。
Sample Input
5 2 0
2 1 1 1
2 1 1 1
3 2 1 1
4 3 1 1
5 4 1 1
2 1 1 1
2 1 1 1
3 2 1 1
4 3 1 1
5 4 1 1
Sample Output
3
HINT
对于30%的数据,0<=W<T<=50,1<=MaxP<=50
对于50%的数据,0<=W<T<=2000,1<=MaxP<=50
对于100%的数据,0<=W<T<=2000,1<=MaxP<=2000
对于所有的数据,1<=BPi<=APi<=1000,1<=ASi,BSi<=MaxP
怎么感觉做单调队列优化着优化着没找到感觉结果巨***儿模糊??
一眼方程f[i][j]表示第i天手里有j张股票,三种转移:
考虑优化,上下界单调,单调队列
然后推柿子,把固定项i提出来,然后剩下的分两种情况讨论即可(雾??复杂度O(nm)
代码如下:
1 //MT_LI 2 #include<cmath> 3 #include<cstdio> 4 #include<cstring> 5 #include<cstdlib> 6 #include<algorithm> 7 using namespace std; 8 int f[2100][2100];//表示第i天手里有j套股票的最优策略 9 /* 10 不买不卖 f[i][j]=f[i-1][j] 11 买入 f[i][j]=f[i-w-1][k]-ap[i]*(j-k)|k>=j-as 12 f[i][j]=f[i-w-1][k]-ap[i]*j+ap[i]*k 13 14 卖出 f[i][j]=f[i-w-1][k]+bp[i]*(k-j)|k<=j+bs 15 */ 16 struct node{ 17 int ap,bp,as,bs; 18 }a[4100];int n,m,w; 19 int head,tail; 20 struct line{ 21 int pos,x; 22 }list[4100]; 23 int main() 24 { 25 scanf("%d%d%d",&n,&m,&w); 26 for(int i=1;i<=n;i++)scanf("%d%d%d%d",&a[i].ap,&a[i].bp,&a[i].as,&a[i].bs); 27 for(int i=1;i<=m;i++)f[0][i]=-99999999; 28 for(int i=1;i<=n;i++) 29 { 30 head=1,tail=0; 31 for(int j=0;j<=m;j++) 32 { 33 f[i][j]=f[i-1][j]; 34 if(i<=w){if(j<=a[i].as)f[i][j]=max(f[i][j],-j*a[i].ap);continue;} 35 while(head<=tail&&list[head].pos<j-a[i].as)head++; 36 if(head<=tail)f[i][j]=max(f[i][j],list[head].x-a[i].ap*j); 37 while(head<=tail&&list[tail].x<f[i-w-1][j]+a[i].ap*j)tail--; 38 list[++tail].x=f[i-w-1][j]+a[i].ap*j; 39 list[tail].pos=j; 40 } 41 head=1,tail=0; 42 if(i>w) 43 { 44 for(int j=m;j>=0;j--) 45 { 46 while(head<=tail&&list[head].pos>j+a[i].bs)head++; 47 if(head<=tail)f[i][j]=max(f[i][j],list[head].x-a[i].bp*j); 48 while(head<=tail&&list[tail].x<f[i-w-1][j]+a[i].bp*j)tail--; 49 list[++tail].x=f[i-w-1][j]+a[i].bp*j; 50 list[tail].pos=j; 51 } 52 } 53 } 54 printf("%d ",f[n][0]); 55 return 0; 56 }