《Subgradients》
Subderivate-wiki
Subgradient method-wiki
《Subgradient method》
Subgradient-Prof.S.Boyd,EE364b,StanfordUniversity
《Characterization of the Subdifferential of Some Matrix Norms 》
定义
我们称(g in mathbb{R}^n)是(f:mathbb{R}^{n} ightarrow mathbb{R})在(xin domf)的次梯度,如果对于任意的(z in domf),满足:
如果(f)是可微凸函数,那么(g)就是(f)在(x)处的梯度。我们将(z)看成变量,那么仿射函数(f(x)+g^T(z-x))是(f(z))的一个全局下估计。这个次梯度的作用,就是在处理不可微函数的时候,提供一个替代梯度的工具,而且,根据定义,沿着次梯度方向,函数的值是非降的:
另外,如果极限存在,有下面的性质,这联系了方向导数和次梯度:
当然,还有从左往右的来的,这里就不讲了。
下图是一个例子,我们可以看到,在存在梯度的地方,次梯度就是梯度,在不可导的地方,次梯度是一个凸集。
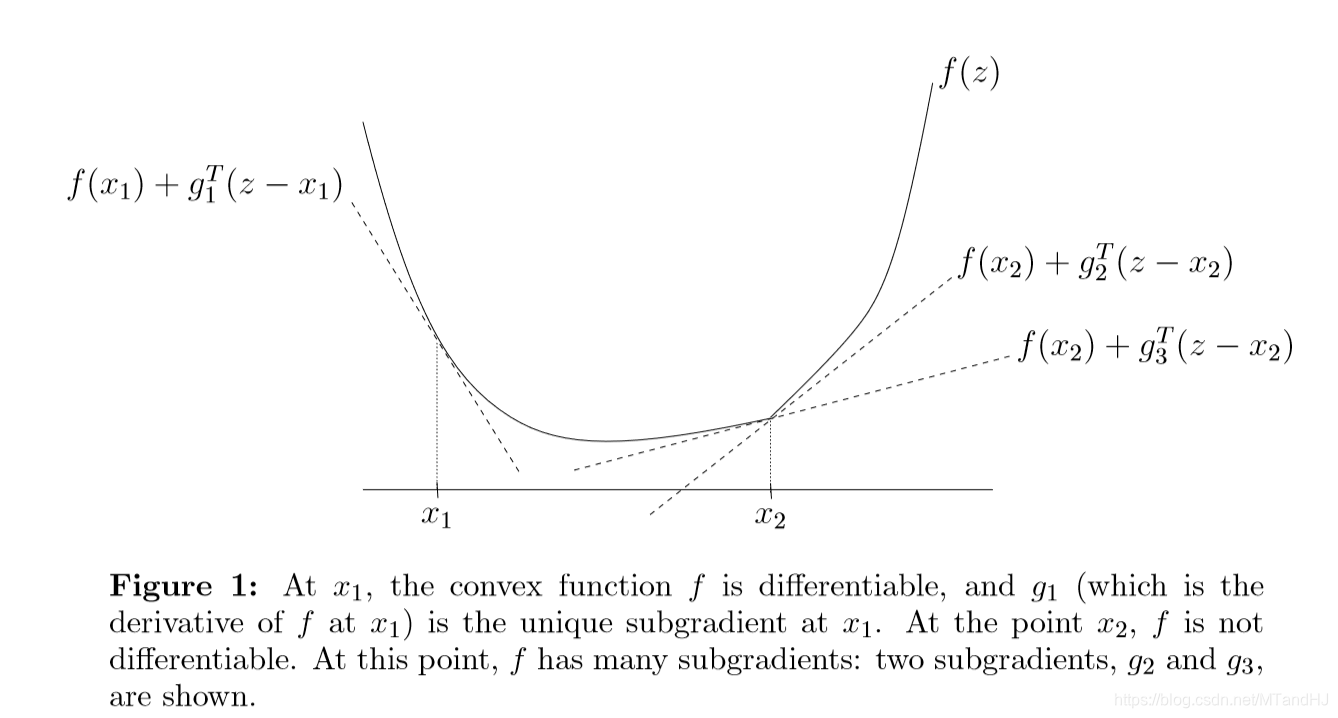
次梯度总是闭凸集,即便(f)不是凸函数,有下面的性质:
下面是(f(x) = |x|)的例子:
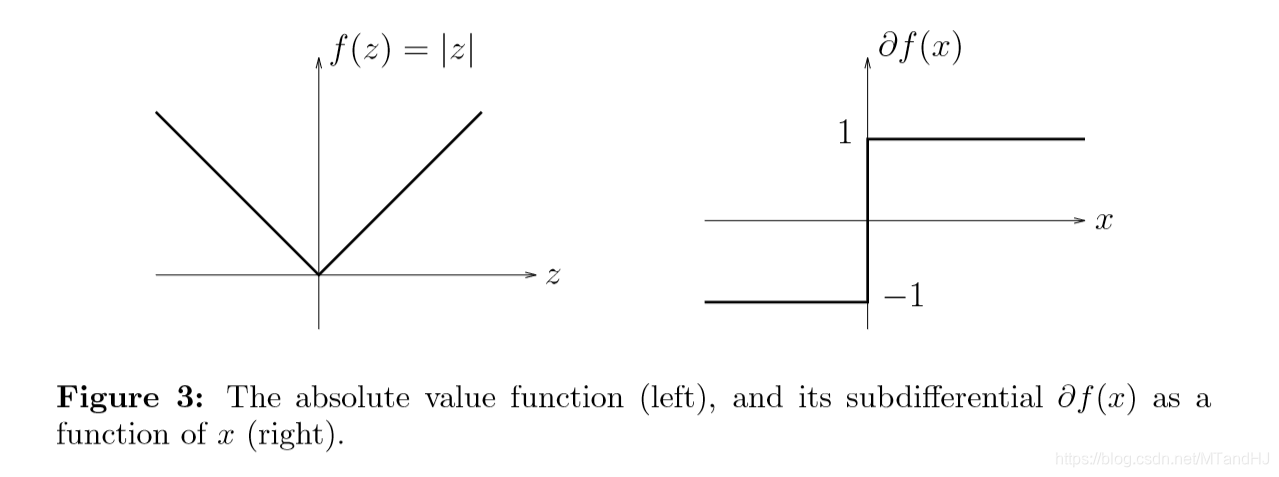
上镜图解释
(g)是次梯度,当且仅当((g, -1))是(f)的上镜图在((x, f(x)))处的一个支撑超平面。
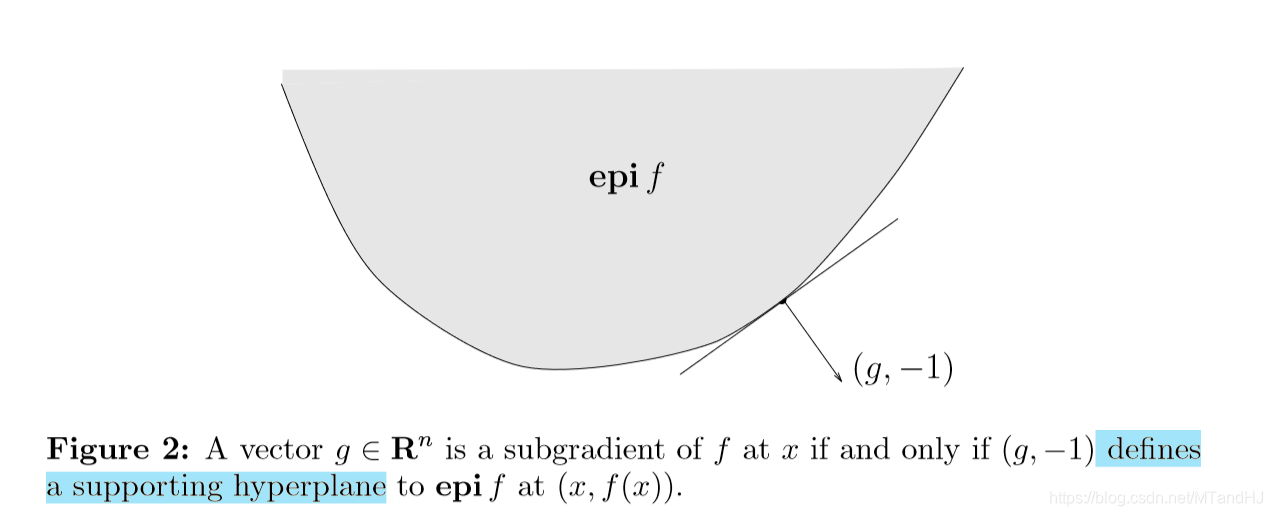
函数(f)的上镜图定义为:
一个函数是凸函数,当且仅当其上镜图是凸集。
我们来证明一开始的结论,即(g)是次梯度,当且仅当((g, -1))是(f)的上镜图在((x, f(x)))处的一个支撑超平面。
首先,若((g, -1))是(f)的上镜图在((x, f(x)))处的一个支撑超平面,则:
对所有((x, t) in mathbf{epi} f)成立,令(t=f(x)),结果便得到。
反过来,如果(g)是次梯度,那么:
又(t ge f(z), (z, t) in mathbf{epi} f),所以:
所以,((g,-1))在((x, f(x)))处定义了一个超平面。
次梯度的存在性
如果(f)是凸函数,且(x in mathbf{int} mathbf{dom} f),那么(partial f(x))非空且闭。根据支撑超平面定理,我们知道,在((x, f(x)))处存在关于(mathbf{epi} f)的一个超平面,设(a in mathbb{R}^n, b in mathbb{R}),则对于任意的((z, t)in mathbf{epi} f)都有:
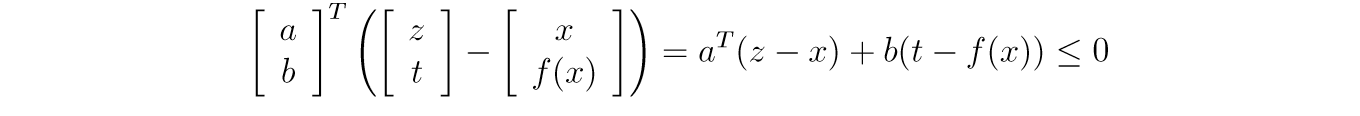
显然,((x, f(x)+epsilon))也符合条件,这意味着(ble0),以及:
对所有(z)成立。
如果(b=0),那么(a=0),不构成超平面,即(b < 0)。
于是:
即(-a/b in partial f(x))
性质
极值
(x^*)是凸函数(f(x))的最小值,当且仅当(f)在(x^*)处存在次梯度且
(f(x) ge f(x^*) Rightarrow 0 in partial f(x^*))
非负数乘 (alpha f(x))
(partial(alpha f) = alpha partial f, alpha ge 0)
和,积分,期望
(f = f_1+f_2ldots+f_n),(f_i,i=1,2,ldots,m)均为凸函数,那么:
(F(x)= int_Y f(x,y) dy), 固定(y), (f(x,y))为凸函数,那么:
不过需要注意的一点是,这里的等号都是对于特定的次梯度,我总感觉(f)的次梯度的集合不止于此,或许会稍微大一点?就是对于和来讲,下面这个式子成立吗?:
至少凸函数没问题吧,凸函数一定是连续函数,且左右导数存在,那么(g)的范围都是固定的。
仿射变换
(f(x))是凸函数,令(h(x)=f(Ax+b))则:
仿梯度
我们知道梯度有下面这些性质:
我认为(注意是我认为!!!大概是是异想天开。)(f)为凸函数的时候,或者(f)为可微(这个时候是一定的)的时候,上面的性质也是存在的。当然,这只是针对某些次梯度。因为当(f)为凸函数的时候,(f)的左右导数都存在,那么:
那么(凸函数的性质)
同理:
而且(k_- le k_+)。
事实上,因为:
所以,容易证明:
容易验证(h(t) = f(x+tv))时关于(t)的凸函数,那么:
同理
一样的分析,我们可以知道:
不好意思,证到这里我证不下去了,我实在不知道结果该是什么。
混合函数

应用
Pointwise maximum
其中(f_i,i=1,2,ldots,m)为凸函数。

(mathbf{Co}(cdot))大概是把里面的集合凸化(我的理解):
第一个例子,可微函数取最大:

我倒觉得蛮好理解的,因为(
abla_i f(x))和(
abla_j f(x))如果都是次梯度,那么根据次梯度的集合都是凸集可以知道(
abla_i f(x),
abla_j f(x))的凸组合也是次梯度。
第二个例子,(ell_1)范数:

我也觉得蛮好理解的。
上确界 supremum
(f_alpha (x))是次可微的。

例子,最大特征值问题:

Minimization over some variables

拟凸函数
