Proximal Algorithms 5 Parallel and Distributed Algorithms

目录

• 问题的结构
• consensus
  • 更为一般的情况
• Exchange 问题
  • Global exchange
  • 更为一般的情况
• Allocation

Proximal Algorithms

这一节，介绍并行算法的实现.

问题的结构

令([n] = {1, ldots, n}). 给定(c subseteq [n]), 让(x_c in mathbb{R}^{|c|})表示向量(xin mathbb{R}^n)的一个子向量(以(c)为指标的对应部分).当(mathcal{P}={c_1, ldots, c_N})满足:

[cup mathcal{P} = [n] \ c_i cap c_j = emptyset, i e j ]

时， 称(mathcal{P})为([n])的一个分割.
函数(f)的(mathcal{P}-)分割满足:

[f(x) = sum_{i=1}^N f_i (x_{c_i}) ]

其中(f_i : mathbb{R}^{|c_i|} ightarrow mathbb{R}).
在这种情况下:

[(mathbf{prox}_f(v))_i = mathbf{prox}_{f_i}(v_i) ]

所以，可以并行计算.

考虑下面的问题：

[mathrm{minimize} quad f(x) + g(x) ]

如果假设(f)是(mathcal{P}-)分割的, 而(g)是(mathcal{Q}-)分割的，那么问题等价于:

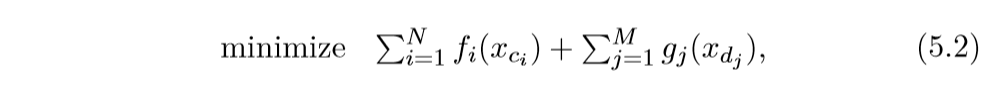
于是ADMM可以并行计算:

consensus

考虑下列问题如何进行并行计算:

[mathrm{minimize} quad f(x) = sum_{i=1}^N f_i (x) ]

一个非常巧妙的变化:

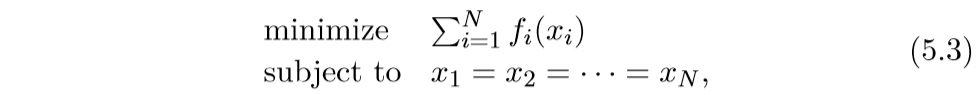
可以看到，这样子，函数就是可分了, 只是多了一个附加条件.
将上面的问题转化为:

[mathrm{minimize} quad sum_{i=1}^N f_i(x_i) + I_{mathcal{C}} (x_1, ldots, x_N) ]

其中(mathcal{C})是consensus set:

[mathcal{C} = {(x_1, ldots, x_N)| x_1 = ldots, =x_N} ]

这样，问题就变成俩个可分函数了, 不过需要注意的是，二者的分割并不相同:

[mathcal{P} = {[n], n+[n], 2n + [n], ldots, (N-1)n + [n]} ]

而(mathcal{Q})，即(I_{mathcal{C}})的分割为:

[mathcal{Q} = {{i, n+i, 2n + i, ldots, (N-1)n + i}|i=1, 2, ldots, n} ]

注: 文中是(i=1, 2, ldots, N)(我认为是作者的笔误).
这个时候的ADMM的第二步，即更新(z)，可以直接为:

[z_i = ar{z} = (1/N) sum_{i=1}^N z_i ]

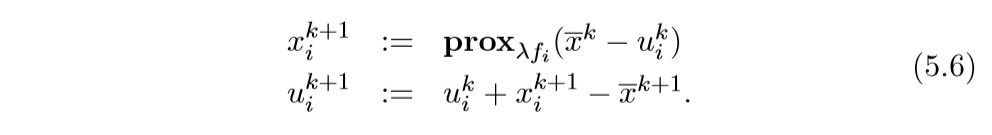
作者贴了一个比较形象的图来表示这种分割:

更为一般的情况

考虑下面的问题:

[mathrm{minimize} quad f(x) = sum_{i=1}^N f_i (x_{c_i}) ]

其中(c_i subseteq [n])， 但是(c_i cap c_j, i e j)并不一定为空集.
进行同样的转换:

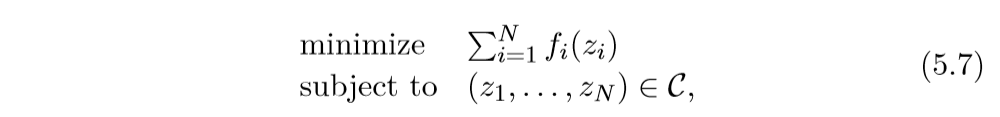
其中

[mathcal{C} = {(z_1, ldots, z_N) | (z_i)_k = (z_j)_k quad if : k in c_i cap c_j} ]

同样等价于:

[mathrm{minimize} quad sum_{i=1}^N f_i(z_i) + I_{mathcal{C}} (z_1, ldots, z_N) ]

相应的有一张比较形象的图：

前一部分的分割是类似的, 后一部分的分割，就是怎么说呢，就像图上的行一样的分.

ADMM为:

其中(F_i = {j in [N] | i in c_j})

Exchange 问题

Global exchange

交换问题具有如下形式:

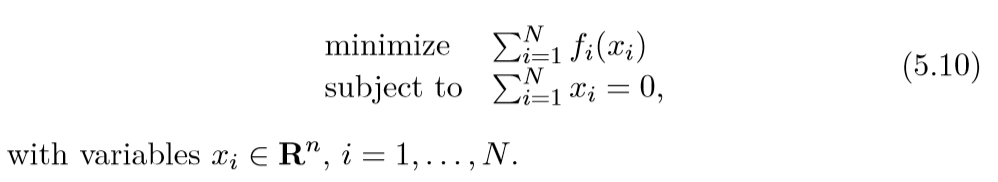
可以用一个实际问题来考量，每个(i)表示一个客户，(x_i)表示每个客户给予或者得到的总量，而(f_i(x_i))表示该客户的效益，(sum_{i=1}^Nx_i=0)这个条件表示，所以客户东西的总量是固定的，即收支平衡.

我们可以将此问题转化为(这个方法太好使了吧):

[mathrm{minimize} quad sum_{i=1}^N f_i(x_i) + I_{mathcal{C}}(x_1, ldots, x_N) ]

其中

[mathcal{C} = {(x_1, ldots, x_N)in mathbb{R}^{nN} | x_1 + x_2 + ldots + x_N=0} ]

我们知道，指示函数的proximal为投影算子, 于是:

[(Pi_{mathcal{C}}(v_1, ldots, v_N))_i = v_i - ar{v} ]

于是ADMM算法为:

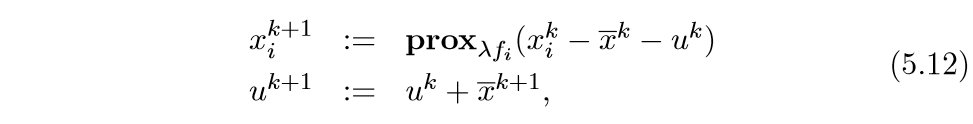
更为一般的情况

有些时候，并不是所有客户都面对同一个市场，所以，每个(x_i)的维度什么对的也有区别:

[mathcal{C} = Big { (z_1, ldots, z_N) Big| sum_{i : k in c_i} (z_i)_k =0 Big } ]

有点和consenus的一般情况比较类似.

Allocation

allocation problem:

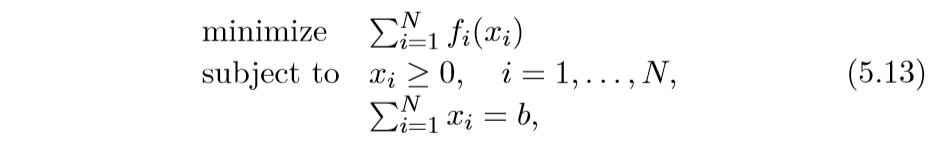
其中(x_i in mathbb{R}^n).

这个问题和交换问题也是相似的，区别在于总量(b)， 而且要求(x_i ge 0).
类似的，我们可以将上面的问题改写为:

[mathrm{minimize} quad sum_{i=1}^N f_i(x_i) + I_{mathcal{C}} (x_1, ldots, x_N) ]

其中:

[mathcal{C} = {(x_1, ldots, x_N)| x_i ge 0, x_1 + ldots + x_N = b} ]

所以相应的算法是:

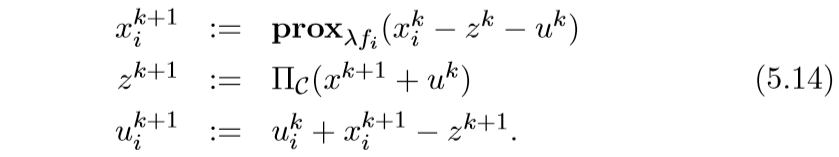
如何进行投影，会在下一节提到， 还有更加一般的情况，比如(sum_{i=1}^N x_i le b).