Deep Linear Networks with Arbitrary Loss: All Local Minima Are Global

目录

• 问题
• 假设和重要结果
• 证明
• 注

Laurent T, Von Brecht J H. Deep linear networks with arbitrary loss: All local minima are global[C]. international conference on machine learning, 2018: 2902-2907.

问题

这篇文章是关于深度学习的一些理论分析.

假设这么一个网络:

[hat{y}^{(i)}=W_LW_{L-1}cdots W_1 x^{(i)}. ]

其中(x)是输入，(W_k)是第(k)层的权重，而(hat{y})是最后的输出. 没错，这篇文章研究的是深度线性网络的性质(没有激活函数). 当然，这样子，无论有多少层，这个网络最后是一个普通线性函数，所以，作者的本意应该只是借此来窥探深度学习的一些性质.

作者证明了，在满足一定条件下，这个深度线性网络，任何局部最优解都是全局最优解.

假设和重要结果

损失函数如此表示:

[mathcal{L}(W_1, ldots, W_L)=frac{1}{N} sum_{i=1}^N ell (hat{y}^{(i)}, y^{(i}) ]

假设

1. (d_k)表示第(k+1)层的神经元个数，即(d_0)表示输入层的维度，(W_k in mathbb{R}^{d_{k-1} imes d_k}), (d_L)表示输出层的维度,
2. (d_k ge min {d_0, d_L}, 0 < k < L),
3. 损失函数关于(hat{y})凸且可微.

定理1：满足上面假设的深度线性网络，任意局部最优都是全局最优.

考虑下面问题p(2):

[min quad f(W_LW_{L-1}cdots W_1), ]

并记(A=W_LW_{L-1}cdots W_1).
则:

定理3:
假设(f(A))是任意的可微函数，且满足:

[min {d_1, ldots, d_{L-1}} ge min {d_0, d_L}, ]

则关于p(2)的任意的极小值点((hat{W}_1, ldots, hat{W}_L))，都将满足:

[ abla f(hat{A})=0 quad hat{A} := hat{W}_L hat{W}_{L-1}cdots hat{W}_1. ]

证明

注意到, 可表示成:

[mathcal{L} (W_1, ldots, W_L)=f(W_Lcdots W_1). ]

则(f(A))是关于(A)的凸的可微函数(注意是关于(A)), 所以，当( abla f(hat{A})=0)的时候，(hat{A})便是(f)，即(mathcal{L})得最小值点. 这意味着，只要我们证明了定理3，也就证明了定理1.

下证定理3:

首先定义:

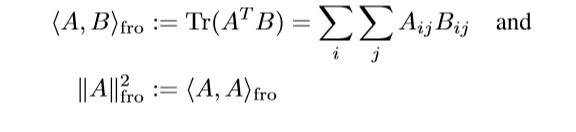
记:

[F(W_1, ldots, W_L) := f(W_L cdots W_1). ]

容易证明(这部分论文中也给出了证明，不在此贴出):

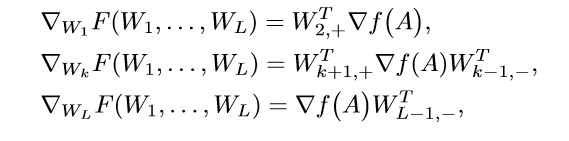
其中:

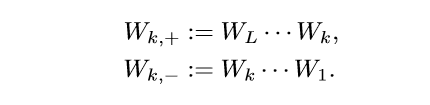
不失一般性，假设(d_Lge d_0), 因为令:

[g(A) := f(A^T) ]

则，(g)定义在(d_0 imes d_L)之上，且(A^T)使得(f)为极小值，当且仅当(A)使得(g)为极小值，所以(d_0, d_L)的地位是相同的，我们可以直接假设(d_L ge d_0).

((hat{W}_1, ldots, hat{W}_L))是最小值点，则存在(epsilon>0)， 使得满足:

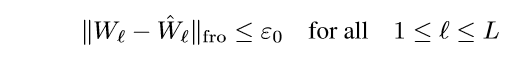
的点满足:

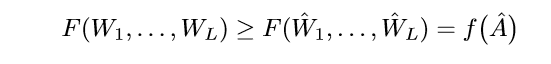
于是:

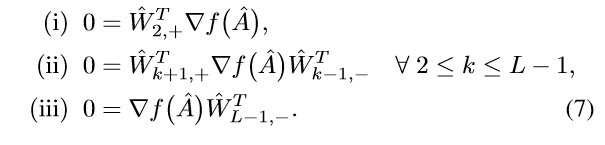
当(mathrm{ker}(hat{W}_{L-1}) = {0})的时候:

[ abla f(hat{A})=0. ]

于是只要证明, (ker(hat{W}_{L-1}) = ot {0})的时候，上式也成立即可.

我们的想法是构造一族极小值点, 满足:

[widetilde{A}=A, ]

通过一些性质，推出( abla f(hat{A})=0).

首先证明，满足:

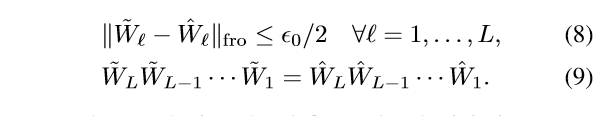
的点都是极小值点.

因为:

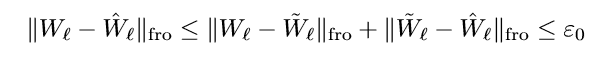
所以:

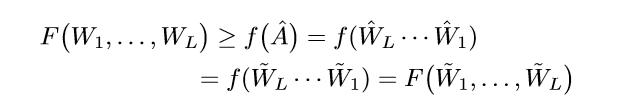
所以(( ilde{W}_1, ldots, ilde{W}_L))也是一个极小值点.

那么如何来构造呢?

可知:

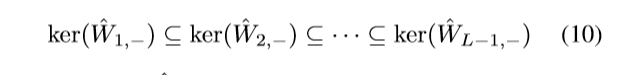
对(hat{W}_{k, -})进行奇异值分解:

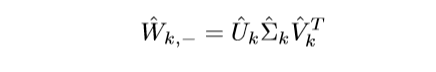
因为(d_k ge d_0, kge1), 所以其分解是这样的:

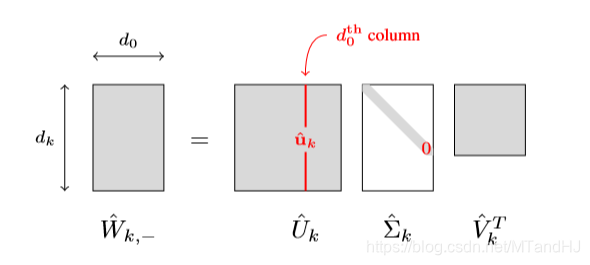
注意到，这里体现了为什么需要(d_kge min {d_L, d_0})， 否则(mathrm{ker}(hat{W}_{k, -}))不可能等于({0})(因为其秩永远小于(d_0)).

假设(k_*)是第一个(mathrm{ker}(hat{W}_{k, -}) = ot{0})的，则下面的构造便是我们所需要的:

其中(hat{u}_{k-1})表示(hat{W}_{k-1, -})奇异值分解(hat{U}_{k-1})的(d_0)列, 很明显，满足(hat{u}_{k-1}^That{W}_{k-1,-}=0, kge k^* + 1).

条件(8)容易证明，用数学归纳法证明(9):
第一项成立，假设第(k)项也成立, 于是

也成立，所以条件成立.

既然满足其构造方式的所有点都是点都是极小值点，那么:

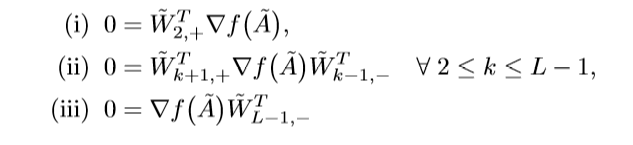
注意，对所有的满足条件的(delta_k, w_k)都成立.
(k_* > 1)的时候可得:

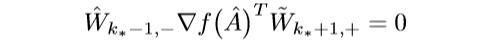
又(mathrm{ker}(hat{W}_{k_*-1,-})={0}), 所以:

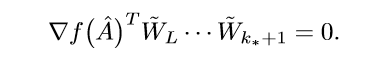
注意到(k_*=1)的时候，也有上面的形式.

首先，令(delta_{k_*+1}=0), 则( ilde{W}_{k_*+1}=hat{W}_{k_*+1}), 于是:

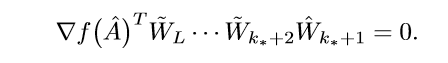
在去任意(delta_{k_*+1} > 0)， 与上式作差可得:

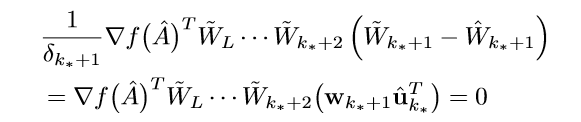
俩边同乘上(hat{u}_{k_*}^T)可得:

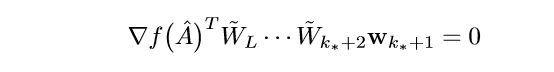
因为(w_{k_*+1})是任意的，所以，左端为0，以此类推，最后可得:

[ abla f( ilde{A})= abla f(hat{A})=0. ]

证毕.

注

我没有把定理2放上来.

有一个方向，定理3中的极小值点改成极大值点，似乎定理也成立，即：
假设(f(A))是任意的可微函数，且满足:

[min {d_1, ldots, d_{L-1}} ge min {d_0, d_L}, ]

则关于p(2)的任意的极大值点((hat{W}_1, ldots, hat{W}_L))，都将满足:

[ abla f(hat{A})=0 quad hat{A} := hat{W}_L hat{W}_{L-1}cdots hat{W}_1. ]

我自己仿照论文的证明是可以证明出来的，不过，既然( abla f(hat{A})=0), 那么(hat{A})依然是(mathcal{L})的最小值点，是不是可以这么认为，(f)压根没有存粹的极大值点.

另外作者指出，极小值点不能改为驻点，因为(A=0)便是一个驻点，但是没有(f(0))必须为0的规定.
此外作者还说明了，为什么要可微等等原因，详情回见论文.