概
本文提出了一种自适应步长的梯度下降方法(以及多个变种方法), 并给了收敛性分析.
主要内容
主要问题:
[ ag{1}
min_x : f(x).
]
局部光滑的定义:
若可微函数(f(x))在任意有界区域内光滑,即
[|
abla f(x) -
abla f(y)| le L_{mathcal{C}} |x-y|, quad forall x, y in mathcal{C},
]
其中(mathcal{C})有界.
本文的一个基本假设是函数(f(x))凸且局部光滑.
算法1 AdGD

定理1 ADGD-L
定理1. 假设(f: mathbb{R}^d ightarrow mathbb{R}) 为凸函数且局部光滑. 则由算法1生成的序列((x^k))收敛到(1)的最优解, 且
[f(hat{x}^k) - f_* le frac{D}{2S_k} = mathcal{O}(frac{1}{k}),
]
其中(hat{x}^k := frac{sum_{i=1}^k lambda_i x^i + lambda_1 heta_1 x^1}{S_k}), (S_k:= sum_{i=1}^k lambda_i + lambda_1 heta).
算法2

在(L)已知的情况下, 我们可以对算法1进行改进.
定理2
定理2 假设(f)凸且(L)光滑, 则由算法(2)生成的序列((x^k))同样使得
[f(hat{x}^k)-f_*=mathcal{O}(frac{1}{k})
]
成立.
算法3 ADGD-accel

这部分没有理论证明, 是作者基于Nesterov中的算法进行的改进.
算法4 Adaptive SGD

这个算法是对SGD的一个改进.
定理4

代码
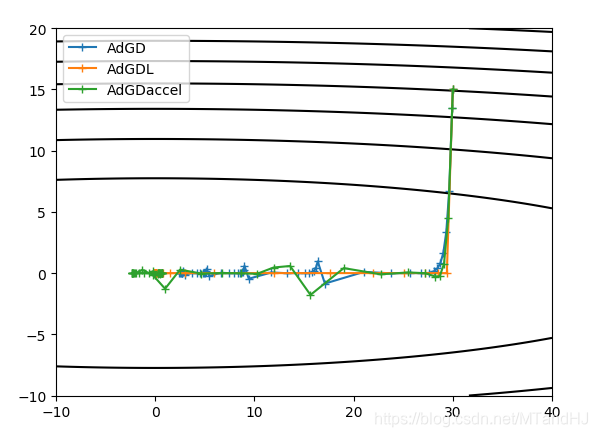
(f(x, y) = x^2+50y^2), 起点为((30, 15)).
"""
adgd.py
"""
import numpy as np
import matplotlib.pyplot as plt
State = "Test"
class FuncMissingError(Exception): pass
class StateNotMatchError(Exception): pass
class AdGD:
def __init__(self, x0, stepsize0, grad, func=None):
self.func_grad = grad
self.func = func
self.points = [x0]
self.points.append(self.calc_one(x0, self.calc_grad(x0),
stepsize0))
self.prestepsize = stepsize0
self.theta = None
def calc_grad(self, x):
self.pregrad = self.func_grad(x)
return self.pregrad
def calc_one(self, x, grad, stepsize):
return x - stepsize * grad
def calc_stepsize(self, grad, pregrad):
part2 = (
np.linalg.norm(self.points[-1]
- self.points[-2]) /
(np.linalg.norm(grad - pregrad) * 2)
)
if not self.theta:
return part2
else:
part1 = np.sqrt(self.theta + 1) * self.prestepsize
return min(part1, part2)
def update_theta(self, stepsize):
self.theta = stepsize / self.prestepsize
self.prestepsize = stepsize
def step(self):
pregrad = self.pregrad
prex = self.points[-1]
grad = self.calc_grad(prex)
stepsize = self.calc_stepsize(grad, pregrad)
nextx = self.calc_one(prex, grad, stepsize)
self.points.append(nextx)
self.update_theta(stepsize)
def multi_steps(self, times):
for k in range(times):
self.step()
def plot(self):
if self.func is None:
raise FloatingPointError("func is not defined...")
if State != "Test":
raise StateNotMatchError()
xs = np.array(self.points)
x = np.linspace(-40, 40, 1000)
y = np.linspace(-20, 20, 500)
fig, ax = plt.subplots()
X, Y = np.meshgrid(x, y)
ax.contour(X, Y, self.func([X, Y]), colors='black')
ax.plot(xs[:, 0], xs[:, 1], "+-")
plt.show()
class AdGDL(AdGD):
def __init__(self, x0, L, grad, func=None):
super(AdGDL, self).__init__(x0, 1 / L, grad, func)
self.lipschitz = L
def calc_stepsize(self, grad, pregrad):
lk = (
np.linalg.norm(grad - pregrad) /
np.linalg.norm(self.points[-1]
- self.points[-2])
)
part2 = 1 / (self.prestepsize * self.lipschitz ** 2)
+ 1 / (2 * lk)
if not self.theta:
return part2
else:
part1 = np.sqrt(self.theta + 1) * self.prestepsize
return min(part1, part2)
class AdGDaccel(AdGD):
def __init__(self, x0, stepsize0, convex0, grad, func=None):
super(AdGDaccel, self).__init__(x0, stepsize0, grad, func)
self.preconvex = convex0
self.Theta = None
self.prey = self.points[-1]
def calc_convex(self, grad, pregrad):
part2 = (
(np.linalg.norm(grad - pregrad) * 2) /
np.linalg.norm(self.points[-1]
- self.points[-2])
) / 2
if not self.Theta:
return part2
else:
part1 = np.sqrt(self.Theta + 1) * self.preconvex
return min(part1, part2)
def calc_beta(self, stepsize, convex):
part1 = 1 / stepsize
part2 = convex
return (part1 - part2) / (part1 + part2)
def calc_more(self, y, beta):
nextx = y + beta * (y - self.prey)
self.prey = y
return nextx
def update_Theta(self, convex):
self.Theta = convex / self.preconvex
self.preconvex = convex
def step(self):
pregrad = self.pregrad
prex = self.points[-1]
grad = self.calc_grad(prex)
stepsize = self.calc_stepsize(grad, pregrad)
convex = self.calc_convex(grad, pregrad)
beta = self.calc_beta(stepsize, convex)
y = self.calc_one(prex, grad, stepsize)
nextx = self.calc_more(y, beta)
self.points.append(nextx)
self.update_theta(stepsize)
self.update_Theta(convex)
config.json:
{
"AdGD": {
"stepsize0": 0.001
},
"AdGDL": {
"L": 100
},
"AdGDaccel": {
"stepsize0": 0.001,
"convex0": 2.0
}
}
"""
测试代码
"""
import numpy as np
import matplotlib.pyplot as plt
import json
from adgd import AdGD, AdGDL, AdGDaccel
with open("config.json", encoding="utf-8") as f:
configs = json.load(f)
partial_x = lambda x: 2 * x
partial_y = lambda y: 100 * y
grad = lambda x: np.array([partial_x(x[0]),
partial_y(x[1])])
func = lambda x: x[0] ** 2 + 50 * x[1] ** 2
fig, ax = plt.subplots()
x = np.linspace(-10, 40, 500)
y = np.linspace(-10, 20, 500)
X, Y = np.meshgrid(x, y)
ax.contour(X, Y, func([X, Y]), colors='black')
def process(methods, times=50):
for method in methods:
method.multi_steps(times)
def initial(methods, **kwargs):
instances = []
for method in methods:
config = configs[method.__name__]
config.update(kwargs)
instances.append(method(**config))
return instances
def plot(methods):
for method in methods:
xs = np.array(method.points)
ax.plot(xs[:, 0], xs[:, 1], "+-", label=method.__class__.__name__)
plt.legend()
plt.show()
x0 = np.array([30., 15.])
methods = [AdGD, AdGDL, AdGDaccel]
instances = initial(methods, x0=x0, grad=grad, func=func)
process(instances)
plot(instances)