@article{xiao2018generating,
title={Generating Adversarial Examples with Adversarial Networks},
author={Xiao, Chaowei and Li, Bo and Zhu, Junyan and He, Warren and Liu, Mingyan and Song, Dawn},
journal={arXiv: Cryptography and Security},
year={2018}}
概
本文利用GAN生成adversarial samples.
主要内容
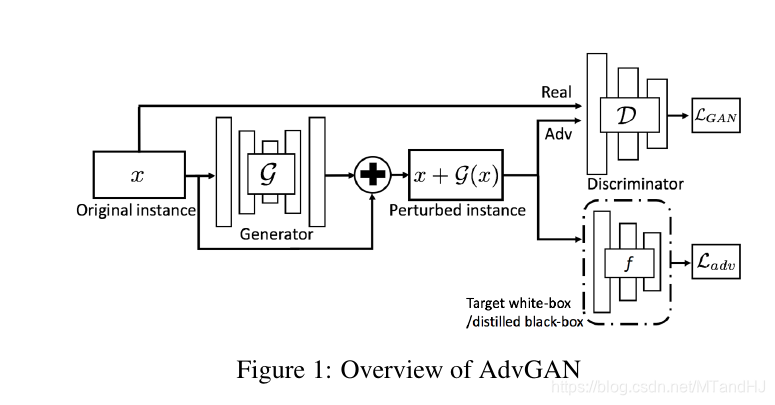
其中(mathcal{G})是生成器, (mathcal{D})是用于判别真假的判别器, 二者都是需要训练的, 而(f)是已知的我们需要攻击的模型(在white-box下是不需要训练的).
训练判别器很普通的GAN是类似的, 即最大化下式:
[ ag{1}
mathcal{L}_{GAN} = mathbb{E}_{x} log mathcal{D}(x) + mathbb{E}_{x} log (1-mathcal{D}(x+mathcal{G}(x))).
]
训练生成器, 除了(mathcal{L}_{GAN}), 还需要
[ ag{2}
mathcal{L}_{adv}^f = mathbb{E}_x ell_f (x+mathcal{G}(x),t),
]
其中(t)是我们所需要的攻击目标(注意这里通过对(ell)的一些额外的选择, 是可以用到untargeted attack的).
[ ag{3}
mathcal{L}_{hinge} = mathbb{E}_x max (0, |mathcal{G}(x)|_2 -c),
]
显然(3)是保证摄动不要太大.
所以训练生成器是最小化
[ ag{4}
mathcal{L}=mathcal{L}_{adv}^f+ alpha mathcal{L}_{GAN} + eta mathcal{L}_{hinge}.
]
black-box 拓展
该方法可以拓展到black-box上, 假设(b(x))是目标网络, 其结构和训练数据都是未知的, 此时我们构建一个替代网络(f(x))用于逼近(b(x)). 利用交替训练, 更新生成器(mathcal{G})和(f).
- 固定(f_{i-1}), 更新(mathcal{G}_i): (mathcal{G}_i)初始化参数为(mathcal{G}_{i-1}), 则
[mathcal{G}_i, mathcal{D}_i = arg min _{mathcal{G}} max_{mathcal{D}} mathcal{L}_{adv}^f+ alpha mathcal{L}_{GAN} + eta mathcal{L}_{hinge}.
]
- 固定(mathcal{G}_i), 更新(f_i): 初始化(f_i)的参数为(f_{i-1}), 则
[f_i=arg min_f mathbb{E}_x mathcal{H} (f(x), b(x)) + mathbb{E}_x mathcal{H} (f(x+mathcal{G}_i(x)), b(x+mathcal{G}_i(x))).
]
其中(mathcal{H})表示交叉熵损失.