AC自动机－－速成版

没办法，学了又忘了，暑假上课没听懂的锅现在要补......

AC自动机的思想:

Ｔｒｉｅ树 + ＫＭＰ，但是有人称它为"树上ＫＭＰ"，我觉得也蛮形象的。

确实也是这样子的，ＡＣ自动机主要就是运用了ＫＭＰ类似的思想以及操作:"失配指针"(字符串匹配都是运用已知信息来减少无效匹配次数......)

同时ＡＣ自动机支持多个模式串的匹配，这样子就运用到了Ｔｒｉｅ树。

(Fail)指针

(Fail)指针的含义:最长的 当前字符串的后缀 在Trie树上的编号

如果一个点(i)的(Fail)指针指向(j)。那么根节点到(j)的字符串是根节点到(i)的字符串的一个后缀。
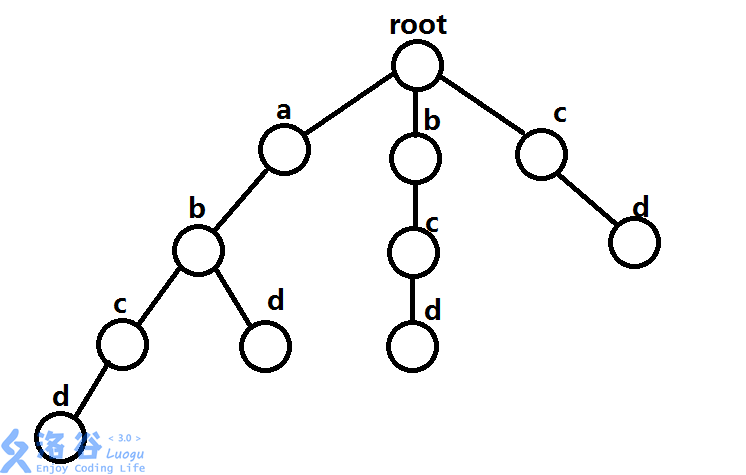
以下面的图为例，我们肉眼就可以发现，最左下的那个"d"的(Fail)指针应该指向中间最下面那个"d"，因为"abcd"的后缀集就有"bcd"这一元素

具体实现((Fail指针的构建方法))

我们明确一点，我们是用Ｔｒｉｅ树上ＢＦＳ的方式来建立(Fail)指针.

• 首先我们把模式串都丢到Trie上面去

(我们默认叶子节点是每个模式串的最后一个字符(真实情况未必是这样！))

ps.上面这张图借用的是luogu用户hicc0305的

显然，每一个点(i)的(Fail)指针指向的点的深度一定是比(i)小的(因为是后缀)。

同时，我们要使得(i)的(Fail)指针指向的位置尽量的深。

分情况讨论:

• 如果(i)的父亲节点不是真正的存在(i)这个子节点(也就是没有真实出现在模式串中，但是我们仍然要遍历)

也就是说比如串"abcb"

我们的第3个字符是c,在第三个字符这一层我们仍然要遍历"a , b , c , d , e , f , g "等等....直到"z"，并且为它们建立(Fail)指针,但是显然只有"c"是真正在文本串中的。

那么对于例如上面的"a,b,d,e,f,g"等等都是并非"真实存在"的，就把当前节点的子节点指向(Fail_{fa})节点的具有相同的值的子节点。

• 如果 (i)的父亲节点确确实实的存在(i)这个子节点(出现在上图中的样子，也就是确确实实出现在一个模式串中的)

不妨令(i)的 父亲 的 (Fail)指针为(Fail_{fa})

令(i)的(Fail)指针指向的点为(Fail_i)，那么我们就会令(Fail_i)等于(Fail_{fa})的儿子节点中与(i)值相同的那个点.

很多人没有介绍这里，蒟蒻我看了十分钟才明白为什么(Fail_{fa})的儿子节点中 一定 会有一个点与(i)值相同

首先(i)节点的父亲节点一定是深度比它浅的,那么父亲节点的(Fail)指针又比父亲节点浅。这样子(Fail_{fa})至少比(i)的深度少了2。

(Fail_{fa})的儿子节点中的与(i)值相同的节点至少深度比(i)少１，满足(Fail)指针的条件。

根据ＢＦＳ，我们默认(i)上层的一定是已经构造好了(Fail)指针的了，而且根据构造方法，对于任何一个文本种类

我们都会遍历，就如同上面说的"abcb"的例子中，遍历第三层的时候我们不仅仅帮"c"建立了(Fail)指针,我们还帮"a,b,d,e,f,g...x,y,z"都建立了(Fail)指针，所以只要是深度比(i)小的节点中，必定有一个节点跟(i)的值相同！

对于构造方法的例子:

我们以图上最左下那个"d"为例，我们假设遍历到了这个节点，因为是BFS，我们默认它上层所有节点已经建成了

(Fail) 指针。这里它的父亲节点"c"的(Fail)指针显然应该指向最中间的"c"节点，那么我们根据构造方法，

(Fail_i)　等于(Fail_{fa})的儿子节点中与(i)值相同的那个点，也就是最中间的"c"的子节点"d"。

(Fail)指针的构建到此结束.按照上面两种情况即可建成(Fail)指针，代码也很好写呀!

康康代码吧

Code

#include <bits/stdc++.h>
using namespace std;
struct {
	int end,Fail;
	int son[26];
}AC[1000005];
char a[1000005],s[1000005];
int cnt = 0,n;
int vis[1000005];
void build()
{
	int len = strlen(s),now = 0;
	for(int i = 0 ; i < len ; i ++)
	{
		int num = s[i] - 'a';
		if(! AC[now].son[num])
			AC[now].son[num] =++cnt;
		now = AC[now].son[num];
	}
	AC[now].end ++;
}

void GetFail()
{
	int now = 0,head = 0,tail = 0;
	for(int i = 0 ; i < 26 ; i ++)
		if(AC[0].son[i] != 0)
			tail ++ , vis[tail] = AC[0].son[i];
	//第一层的Fail指针只能指向Ｒｏｏｔ(这里是0号节点)，优先进入队列
	while(head < tail)
	{
		head ++;
		int v = vis[head];
		int Fail = AC[v].Fail;//这个点的Fail指针　
		for(int i = 0 ; i < 26 ; i ++)//遍历当前点的儿子节点
		{
			if(AC[v].son[i])//如果"真实存在这个点"
			{
				AC[AC[v].son[i]].Fail = AC[Fail].son[i];
				tail ++;
				vis[tail] = AC[v].son[i];//记得入队
			}
			else AC[v].son[i] = AC[Fail].son[i];
			//否则就把这个儿子节点接到Fail[fa]的相同值的儿子节点上
		}
	}
	return ;//这就完事了......
}

void GetAns()
{
	int len = strlen(a),now = 0 , ans = 0;
	for(int i = 0 ; i < len  ; i ++)
	{
		int num = a[i] - 'a';
		now = AC[now].son[num];
		for(int u = now ; AC[u].end != -1 && u ; u = AC[u].Fail)
                  //u == 0 表示访问到了一个虚节点，那么匹配失败,AC[u] == -1表示当前已经匹配过了，就跳走
		{
			ans += AC[u].end;
			AC[u].end = -1;
		}
	}
	cout << ans << endl;
	return ;
}

int main()
{
	cin >> n;
	for(int i = 1 ; i <= n ; i ++)
	{
		cin >> s;
		build();
	}
	GetFail();
	cin >> a;
	GetAns();
	return 0;
}

ＡＣ自动机加强版:

给你n个模式串以及1个文本串，你需要求出哪个模式串在文本串中出现次数最多，输出最多出现的次数以及出现次数最多的模式串.

思路

修改一下end存的东西以及查询答案的方式就行了(char数组开小了居然没有RE而是输出超限？不知道输出了些啥(数组越界居然会影响这么多东西)......)

#include <bits/stdc++.h>
using namespace std;
int n;
int cnt = 0,coun[500],T = 0;
char s[1505];
char t[1500005];
char ans[155][75];
int vis[1000005];
#define Faili AC[AC[v].son[i]].Fail
struct {
	int end,Fail;
	int son[26];
	void clea()
	{
		end = Fail = 0;
		for(int i = 0 ; i < 26 ; i ++)
			son[i] = 0;
	}
}AC[1000005];

void build(int k)
{
	int len = strlen(s) , now  = 0;
	for(int i = 0 ; i < len ; i ++)
	{
		int num = s[i] - 'a';
		if(AC[now].son[num] == 0)
			cnt ++ , AC[now].son[num] = cnt;
		now = AC[now].son[num];
		ans[k][i] = s[i];
	}
	AC[now].end = k;
	return ;
}

void GetFail()
{
	int head = 0 , tail = 0 , now = 0;
	for(int i = 0 ; i < 26 ; i ++)
		if(AC[0].son[i])tail++,vis[tail] = AC[0].son[i];
	while(head < tail)
	{
		head++;
		int v = vis[head];
		int Failfa = AC[v].Fail;
		for(int i = 0 ; i < 26 ; i ++)
		{
			if(AC[v].son[i])
			{
				Faili = AC[Failfa].son[i];
				tail ++;
				vis[tail] = AC[v].son[i];
			}
			else AC[v].son[i] = AC[Failfa].son[i];
		}
	}
	return ;
}

void clean()
{
	for(int i = 0 ; i <= cnt ; i ++)
		AC[i].clea();
	for(int i = 1 ; i <= T ; i ++)
	{
		coun[i] = 0;
		memset(ans[i],0,sizeof(ans[i]));
	}
	cnt = 0;T = 0;
}

void Compare()
{
	int len = strlen(t) , now = 0;
	for(int i = 0 ; i < len  ;i ++)
	{
		int num = t[i] - 'a';
		now = AC[now].son[num];
		int u = now;
		for(; u ; u = AC[u].Fail)
		{
			coun[AC[u].end]++;
		}
	}
}

int main()
{
	while(1)
	{
		cin >> n;
		if(n == 0)break;
		clean();
		
		while(n)
		{
			cin >> s;
			T++;
			build(T);
			memcpy(ans[T],s,sizeof(s));
			n--;
		}
		
		GetFail();
		cin >> t;
		Compare();
		int M = 0;
		for(int i = 1 ; i <= T ; i ++)
			M = max(M,coun[i]);
		cout << M << endl;
		for(int i = 1 ; i <= T ; i ++)
			if(coun[i] == M)cout << ans[i] << endl;
	}
	return 0;
}