多项式加法和乘法的实现

多项式的表示可以使用数组也可以使用链表

• 数组表示起来简单，调试方便。但需要事先确定数组的大小。
• 链表表示起来动态性强，但编程复杂，调试起来困难。

为了提高对链表的操作，后面介绍的程序，均使用链表来完成。

注意：下列链表没有头节点

//多项式的加法和乘法
#define  _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

struct PolyNode 
{
	int Coef;
	int Expon;
	struct PolyNode* Next;  //指向下一个节点
};

void Attach(int coef,int expon,struct PolyNode** PtrRear)
{
	struct PolyNode* p;
	p = (struct PolyNode*)malloc(sizeof(struct PolyNode));
	p->Coef = coef;
	p->Expon = expon;
	p->Next = NULL;
	(*PtrRear)->Next = p;
	(*PtrRear) = p;  //修改PtrRear的值
}

struct PolyNode* ReadPoly()
{
	int N;  //存储多项式的项数
	int c;  //多项式的系数
	int e;  //多项式的指数
	struct PolyNode* p;  //表头
	struct PolyNode* Rear;
	struct PolyNode* t;
	p = (struct PolyNode*)malloc(sizeof(struct PolyNode));
	p->Next = NULL;
	Rear = p;
	scanf("%d",&N);
	while (N--)
	{
		scanf("%d %d",&c,&e);
		Attach(c,e,&Rear);
	}
	t = p;
	p = p->Next;
	free(t);  //删除临时生成的头节点
	return p;
}
//作用：比较两个指数的大小
//返回值： e1 > e2 返回 1
//         e1 < e2 返回 -1
//         e1 = e2 返回 0
int Compare(int e1,int e2)
{
	if (e1 > e2)
	{
		return 1;
	}
	else if (e1 < e2)
	{
		return -1;
	}
	else
	{
		return 0;
	}
}

//将两个多项式相加
struct PolyNode* PolyAdd(struct PolyNode* P1, struct PolyNode* P2)
{
	struct PolyNode* rear;
	struct PolyNode* front;
	struct PolyNode* temp;
	int sum;

	//为方便表头插入，先产生一个临时空节点作为结果多项式链表头
	rear = (struct PolyNode*)malloc(sizeof(struct PolyNode));
	front = rear;

	while (P1 && P2)  //当两个多项式都有非零项待处理时
	{
		switch (Compare(P1->Expon, P2->Expon))
		{
		case 1:
			Attach(P1->Coef,P1->Expon,&rear);
			P1 = P1->Next;
			break;
		case -1:
			Attach(P2->Coef, P2->Expon, &rear);
			P2 = P2->Next;
			break;
		case 0:
			sum = P1->Coef + P2->Coef;
			if (sum)
			{
				Attach(sum,P1->Expon,&rear);
			}
			P1 = P1->Next;
			P2 = P2->Next;
			break;
		}
	}
	//将未处理完的另一个多项式的所有节点依次复制到结果多项式中去
	for (;P1;P1 = P1->Next)
	{
		Attach(P1->Coef,P1->Expon,&rear);
	}
	for (; P2; P2 = P2->Next)
	{
		Attach(P2->Coef, P2->Expon, &rear);
	}
	rear->Next = NULL;
	temp = front;
	front = front->Next; //令front指向结果多项式第一个非零项
	free(temp);
	return front;
}
//将两个多项式相乘
struct PolyNode* PolyMult(struct PolyNode* P1, struct PolyNode* P2)
{
	struct PolyNode* rear;
	struct PolyNode* P;
	struct PolyNode* t1 = P1;
	struct PolyNode* t2 = P2;
	struct PolyNode* t;
	int sumc;
	int sume;

	if (NULL == P1 || NULL == P2)
	{
		return NULL;
	}
	//产生一个临时空节点作为结果多项式链表头
	P = (struct PolyNode*)malloc(sizeof(struct PolyNode));
	rear = P;
	while (t2)
	{
		//先用P1的第一项乘以P2得到P
		Attach(t1->Coef * t2->Coef,t1->Expon + t2->Expon,&rear);
		t2 = t2->Next;
	}
	t1 = t1->Next;

	while (t1)
	{
		rear = P;
		t2 = P2;
		while (t2)
		{
			sumc = t1->Coef * t2->Coef;  //系数相乘
			sume = t1->Expon + t2->Expon;  //指数相加
			while (rear->Next && rear->Next->Expon > sume)
			{
				rear = rear->Next;
			}
			if (rear->Next && rear->Next->Expon == sume)
			{
				if (rear->Next->Coef + sumc)
				{
					//rear->Next->Coef + sumc != 0
					rear->Next->Coef = rear->Next->Coef + sumc;
				}
				else
				{
					//rear->Next->Coef + sumc = 0
					//删除一个节点
					t = rear->Next;
					rear->Next = t->Next;
					free(t);
				}
			}
			else //rear->Next->Expon < sume
			{
				//向链表中插入新的节点
				t = (struct PolyNode*)malloc(sizeof(struct PolyNode));
				t->Coef = sumc;
				t->Expon = sume;
				t->Next = NULL;
				t->Next = rear->Next;
				rear->Next = t;

				rear = rear->Next;
			}
			t2 = t2->Next;
		}
		t1 = t1->Next;
	}
	t2 = P;
	P = P->Next;
	free(t2);
	return P;
}
//将多项式输出
void PrintPoly(struct PolyNode* P)
{
	int flag = 0;
	if (NULL == P)
	{
		printf("0 0
");
	    return 0;
	}
	while (P)
	{
		if (!flag)
		{
			flag = 1;
		}
		else
		{
			printf(" ");
		}
		printf("%d %d", P->Coef, P->Expon);
		P = P->Next;
	}
	printf("
");
}

int main()
{
	struct PolyNode* P1;
	struct PolyNode* P2;
	struct PolyNode* PP;
	struct PolyNode* PS;

	P1 = ReadPoly();
	P2 = ReadPoly();
	PP = PolyAdd(P1, P2);
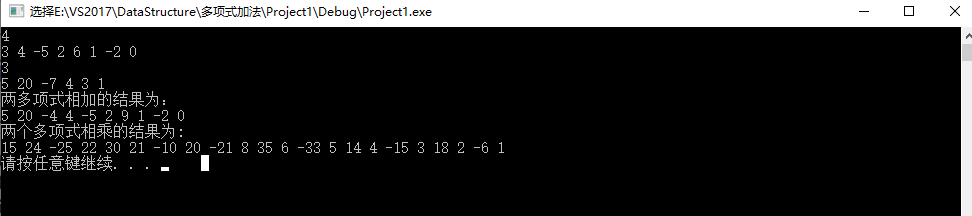
	printf("两多项式相加的结果为：
");
	PrintPoly(PP);
	printf("两个多项式相乘的结果为:
");
	PS = PolyMult(P1,P2);
	PrintPoly(PS);
	system("pause");
	return 0;
}

参考资料：
1 《数据结构》 陈越主编
2 慕课网 《数据结构》 陈越老师，何钦铭老师主讲