63. Unique Paths II

• 思路1

这个题目第一个思路还是用DFS，和第62题一样，但是在递归的时候需要判断有无障碍物。因为第62题用的DFS，Leetcode提示Time Limit Exceeded，所以这道题没有尝试DFS的做法，而是直接使用了DP。

• 思路2

根据第62题可以得到状态转移方程为dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，其中dp[i][j] 表示到当前位置不同的走法的个数。在本题中，状态转移方程因为障碍物的存在略有变化。另外由于障碍物的存在，数组的初始化也有一些不同。

先看第一种情况，障碍物在边上的情况：

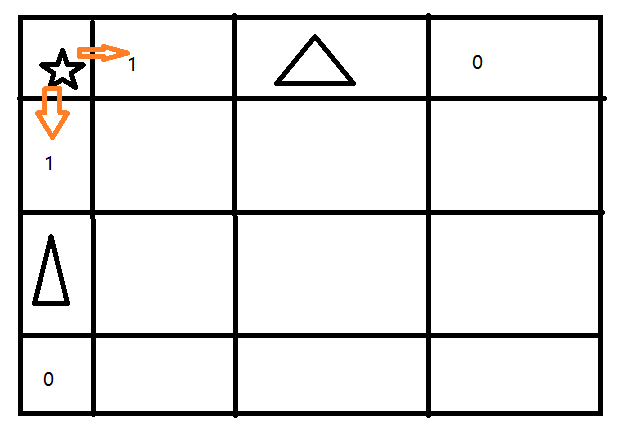
障碍物后面的dp[][]都应该被初始化为0，因为机器人只能向左走或向右走，而在边上的这种情况，机器人没有办法走到。

障碍物在中间：

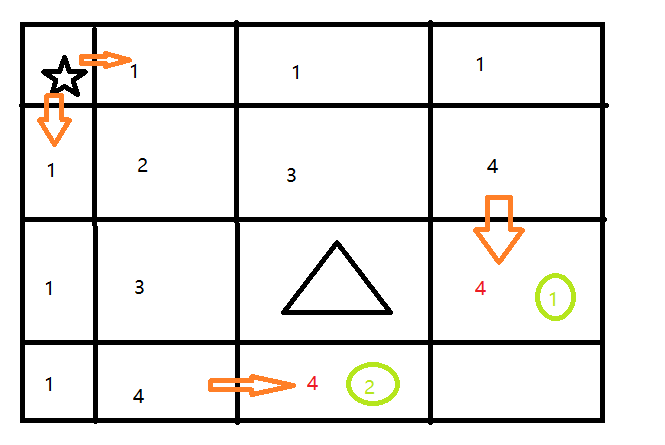
在这种情况下，受到障碍物影响的是障碍物左边的1号和障碍物下边的2号，1号由于障碍物的影响，只能从上往下走，所以可以走到1号的不同走法的个数是1号上方的小格子决定的。2号受到障碍物的影响，只能从2号的左边走到，因此走到2号的不同走法的个数是由2号左边的小格子决定的。

因此状态转移方程如下：

dp[i][j] = dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; dp[i][j]的左边和上边都没有障碍物的情况。
dp[i][j] = dp[i][j - 1]; dp[i][j]的左边有障碍物的情况
dp[i][j] = dp[i - 1][j]; dp[i][j]的上面有障碍物的情况。

C++代码实现如下：

class Solution {
public:
	int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
	{
		//维护一个二维数组
		double row = obstacleGrid.size();
		double col = obstacleGrid.at(0).size();

		vector<vector<double>> dp(row, vector<double>(col));
		//初始化dp数组
		for (int i = 0;i < 1;i++)
		{
			for (int j = 0;j < col;j++)
			{
				if (obstacleGrid[i][j] == 0)
				{
					dp[i][j] = 1;
				}
				else if (obstacleGrid[i][j] == 1)
				{
					dp[i][j] = 0;
					for (;j < col;j++)
					{
						dp[i][j] = 0;
					}
				}
			}
		}
		for (int j = 0; j < 1; j++)
		{
			for (int i = 0; i < row; i++)
			{
				if (obstacleGrid[i][j] == 0)
				{
					dp[i][j] = 1;
				}
				else if (obstacleGrid[i][j] == 1)
				{
					dp[i][j] = 0;
					for (; i < row; i++)
					{
						dp[i][j] = 0;
					}
				}
			}
		}
		for (int i = 1;i < row;i++)
		{
			for (int j = 1;j < col;j++)
			{
				if (obstacleGrid[i][j] == 1)
				{
					dp[i][j] = 0;
				}
				else
				{
					dp[i][j] = 1;
				}
			}
		}
		//根据状态方程和障碍物判断路径
		for (int i = 1;i < row;i++)
		{
			for (int j = 1;j < col;j++)
			{					
				if (dp[i][j] == 0)
				{
					continue;
				}
				else
				{
					if (dp[i-1][j] == 0)
					{
						dp[i][j] = dp[i][j - 1];
					}
					else if (dp[i][j - 1] == 0)
					{
						dp[i][j] = dp[i - 1][j];
					}
					else
					{
						dp[i][j] = dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
					}
				}
			}
		}
		return dp[row - 1][col - 1];
	}
};