如图所示,在平面四边形(ABCD)中,(AB=1),(BC=2),( riangle ACD)为正三角形,则( riangle BCD)面积的最大值为(underline{qquadqquad}).
解析: 将(BC)边固定,则(A)点在以(B)为圆心,(1)为半径的圆上运动, 由于( riangle ACD)为正三角形,因此
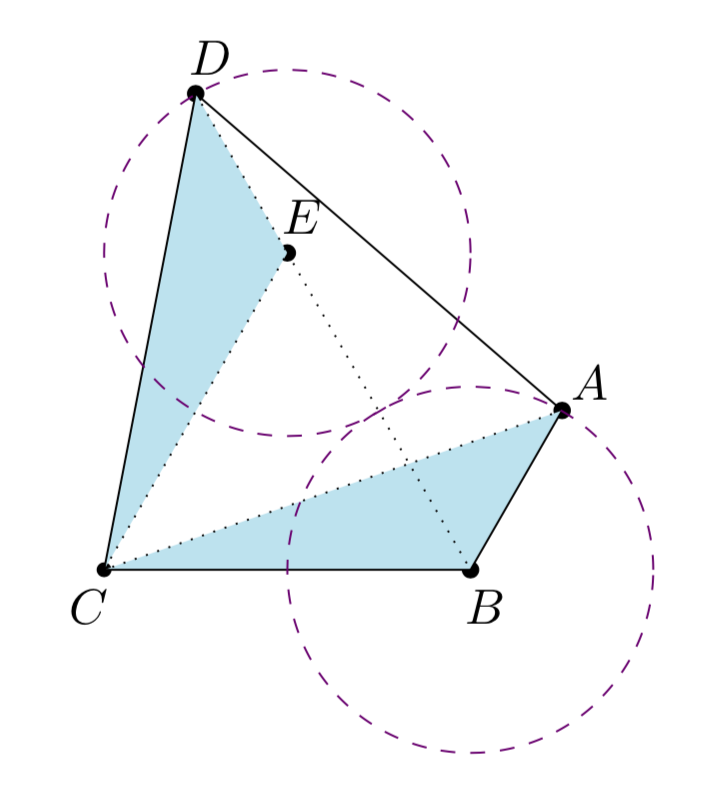
(D)点是在以(E)点为圆心,(1)为半径的圆上运动,其中(E)点是把(B)点绕着(C)点逆时针旋转(60^circ)所得的点.因此显然当(D)点位于圆(E)的上端顶点时,( riangle BCD)的面积最大,且此时面积最大值为$$
S=dfrac{1}{2}cdot |BC|cdot left(dfrac{sqrt{3}}{2}|BC|+1
ight)=sqrt{3}+1.$$