每日一题_191201

一项智力游戏的规则如下:在(4 imes 4)的宫格中放上(8)面完全相同的标志旗帜,每行每列有且只有(2)面旗帜,则不同的放法有(underline{qquadqquad}) 种.
解析
法一 由于(4 imes 4)的宫格每一列只插有两面旗子(青色),

因此这四列的类型总数共计( m{C}_4^2=6)种,如图所示,分别记为基因( m{A-F}). 从这六个类型中选择四个组成一个"基因型".那么这个``基因型''有且仅有两类,第一类基因型包含(2)个基因,第二类基因型包含(4)个基因,分别记为( m{XXYY})型和( m{XYZW})型.
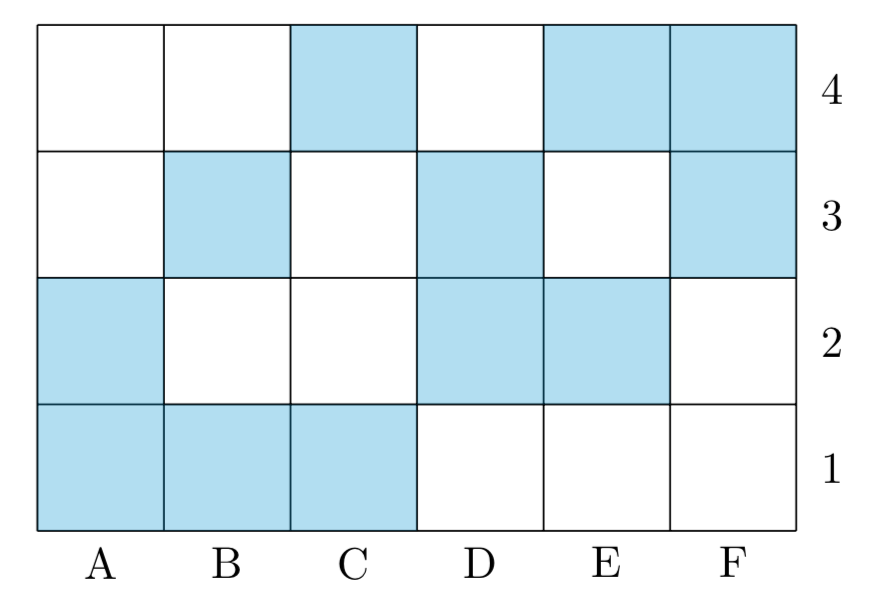
情形一 ( m{XXYY})型 由于( m{X})一旦确定,则( m{Y})随之唯一确定,因此该种情形( m{X})与( m{Y})的组合种数有(3)种.而每一种组合都对应( m{C}_4^2=6)种排列,因此 ( m{XXYY})型的个数共计(3cdot 6=18)种.
情形二 ( m{XYZW})型 对于该种情形,分两步解决.
第一步 确定(4 imes 4)宫格中四列的类型 在选择的时候必然是从( m{ABC})中选(2)种,再从( m{DEF})中选(2)种,并且前两种一旦确定下来,则后两种随之唯一确定,因此在选择基因这件事情上,满足题意的选法有( m{C}_3^2=3)种.
第二步 将选定的不同四列排序 四列模型各不相同,考虑四列之间的顺序差异共计( m{A}_4^4=24)种.
因此( m{XYZW})型的个数共计(3cdot 24=72)种.
综上,所有满足题意的旗帜放法有(18+72=90)种.
法二 逐行确定放法,共计$$ m{C}_4^{2cdotleft[left( m{C}_2}2 ight)^{2+left( m{C}_2}1 m{C}_2^1 ight)cdot 2+ m{C}_2^{2cdot m{C}_4}2 ight]cdot m{C}_2^2=90.$$