Our Journey of Dalian Ends 最小费用最大流

链接：https://nanti.jisuanke.com/t/16959

题意：从大连出发，经途经上海，然后最终到达西安，每个地方只能经过一次，然后给出一些无向有权变，求最短的距离。

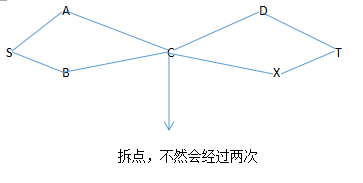
题解：最小费用最大流，要抽象出模型来。因为每个地方只能经过一次，因此要拆点，将每个地方作为一个点，将这个点拆成入点和出点（详见如图的反例），然后连边。从上海出发连边，容量是1，每条边的花费就是这条边的权值，出点和入点之间的边的花费为0。建立超级汇点T,从西安和大连分别连向汇点容量为1的边，花费为0。原来点的序号为（1----n），拆后点的序号为（1+n-----n+n）;

详见代码：（会被队友嫌弃的板子）

#include <stdio.h>
#include <algorithm>
#include <math.h>
#include <string.h>
#include <vector>
#include <queue>
#include <map>
#include <stack>
#include <iostream>
#define pi acos(-1.0)
#define INF 0x3f3f3f3f
using namespace std;
#define ll long long
const double INFINITE= 1e18;
#define MAX_NODE 10010
#define MAX_EDGE_NUM 400005
struct Edge{

    ll to;

    ll vol;

    ll cost;

    ll next;

};

Edge gEdges[MAX_EDGE_NUM];

ll gHead[MAX_NODE];

ll gPre[MAX_NODE];

ll gPath[MAX_NODE];

ll gDist[MAX_NODE];

ll gEdgeCount;
void init()
{
    memset(gHead,-1,sizeof gHead);
    gEdgeCount=0;
}
void InsertEdge(ll u, ll v, ll vol, ll cost){

    gEdges[gEdgeCount].to = v;

    gEdges[gEdgeCount].vol = vol;

    gEdges[gEdgeCount].cost = cost;

    gEdges[gEdgeCount].next = gHead[u];

    gHead[u] = gEdgeCount++;



    gEdges[gEdgeCount].to = u;

    gEdges[gEdgeCount].vol = 0;         //vol为0，表示开始时候，该边的反向不通

    gEdges[gEdgeCount].cost = -cost;    //cost 为正向边的cost相反数，这是为了

    gEdges[gEdgeCount].next = gHead[v];

    gHead[v] = gEdgeCount++;

}
//假设图中不存在负权和环,SPFA算法找到最短路径/从源点s到终点t所经过边的cost之和最小的路径

bool Spfa(ll s, ll t){
    memset(gPre, -1, sizeof(gPre));
    memset(gDist, 0x7F, sizeof(gDist));
    gDist[s] = 0;
    queue<ll> Q;
    Q.push(s);
    while (!Q.empty()){//由于不存在负权和环，因此一定会结束

        ll u = Q.front();
        Q.pop();
        for (ll e = gHead[u]; e != -1; e = gEdges[e].next){
            ll v = gEdges[e].to;
            if (gEdges[e].vol > 0 && gDist[u] + gEdges[e].cost < gDist[v]){
                gDist[v] = gDist[u] + gEdges[e].cost;
                gPre[v] = u; //前一个点
                gPath[v] = e;//该点连接的前一个边
                Q.push(v);
            }
        }
    }
    if (gPre[t] == -1)  //若终点t没有设置pre，说明不存在到达终点t的路径

        return false;

    return true;

}
ll MinCostFlow(ll s, ll t){

    ll cost = 0;

    ll flow = 0;

    while (Spfa(s, t)){
        ll f = INFINITE;

        for (ll u = t; u != s; u = gPre[u]){

            if (gEdges[gPath[u]].vol < f)

                f = gEdges[gPath[u]].vol;

        }

        flow += f;
        cost += gDist[t];
        //printf("cost %d
",cost);
        for (ll u = t; u != s; u = gPre[u]){
            gEdges[gPath[u]].vol -= f;   //正向边容量减少
            gEdges[gPath[u]^1].vol += f; //反向边容量增加
        }
    }
    if(flow!=2) return -1;
    return cost;

}
map<string,ll> jl;
int u[MAX_NODE],v[MAX_NODE],w[MAX_NODE];
int  main()
{
    //freopen("C:\Users\Administrator\Desktop\a.txt","r",stdin);
    ios::sync_with_stdio(false);
    //freopen("C:\Users\Administrator\Desktop\b.txt","w",stdout);
    ll T,n,m;
    cin>>T;
    while(T--)
    {
        m=3;
        cin>>n;
        init();
        jl.clear();
        string c1="Shanghai",c2="Xian",c3="Dalian";
        jl[c1]=1,jl[c2]=2,jl[c3]=3;
        for(int i=0;i<n;i++)
        {
            string c1,c2;
            int tp1,tp2;
            ll a;
            cin>>c1>>c2>>a;
            if(jl[c1]) tp1=jl[c1];
            else jl[c1]=++m;
            if(jl[c2]) tp2=jl[c2];
            else jl[c2]=++m;
            tp1=jl[c1],tp2=jl[c2]; //先将边存储起来
            u[i]=tp1,v[i]=tp2,w[i]=a;
        }
        int T=2*m+1;
        for(int i=0;i<n;i++)
            if(u[i]==1) InsertEdge(u[i],v[i],1,w[i]);
            else if(v[i]==1) InsertEdge(v[i],u[i],1,w[i]);
            else InsertEdge(u[i]+m,v[i],1,w[i]),InsertEdge(v[i]+m,u[i],1,w[i]);
        for(int i=2;i<=m;i++) InsertEdge(i,i+m,1,0);//拆点之后的出点和入点
        InsertEdge(2+m,T,1,0);InsertEdge(3+m,T,1,0);//大连和西安连向汇点
        ll ans=MinCostFlow(1,T);
        printf("%lld
",ans);
    }
    return 0;
}