实践题目:图的广度优先遍历
题目要求:由课上在班课资源里得到的图进行广度优先遍历,从每一个顶点出发得到结果。
附图: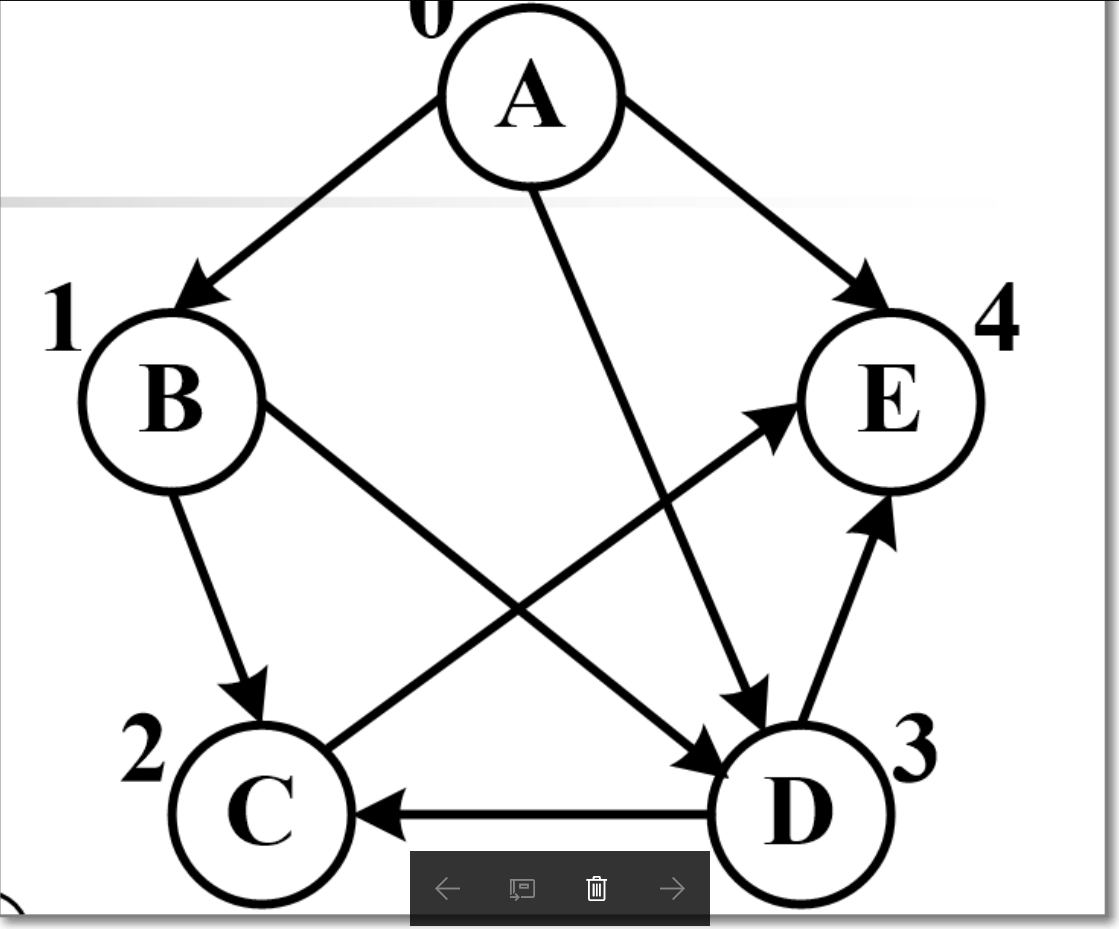
首先需要学习广度优先遍历的定义及方法
概念:广度优先遍历是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,则称为广度优先遍历。其基本思想为:
1、从图中某个顶点V0出发,并访问此顶点;
2、从V0出发,访问V0的各个未曾访问的邻接点W1,W2,…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点;
3、重复步骤2,直到全部顶点都被访问为止。
同样,广度优先遍历也对应出很多性质:可以通过广度优先遍历生成树,在广度优先遍历中,如果将每次"前进"(纵深)路过的(将被访问的)结点和边都记录下来,就得到一个子图,该子图为以出发点为根的树,称为广度优先生成树。这种情况与深度优先遍历类似。可以解决最短路径问题:从v0出发广度优先遍历图,将得到v0到它的各个可达到的路径。我们这里定义路径上的边的数目为路径长度。与深度优先遍历不同,广度优先遍历得到的v0到各点的路径是最短路径。
在对应到这个题目中,则基于广度优先遍历原则可以得到结果:

因为广度优先遍历属于以辐射状覆盖较广的范围,则可得到以上结果。