不连续的处理很麻烦
导致序列DP又找不到优秀的子问题
自底向上考虑?
建立小根堆笛卡尔树
每个点的意义是:高度是(自己-father)的横着的极大矩形
子问题具有递归的优秀性质
f[i][j]i为根子树,放j个
儿子背包合并
考虑本层的矩形放多少个
枚举一共放t个,本层放j个
对于子树里的放置的t-j个,不论怎么放,一定占据了t-j列,剩下W[i]-(t-j)个位置
转移是:
https://blog.csdn.net/qq_39972971/article/details/79359547
当前节点的:枚举放多少个、占哪些行、占哪些列、具体先后顺序。
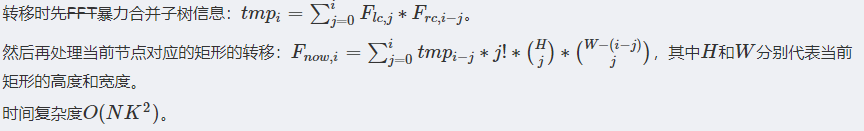
代码:
C(n,m)时刻注意n>=0&&m>=0&&n>=m否则<0越界还看不出来调死
#include<bits/stdc++.h> #define reg register int #define il inline #define int long long #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=505; const int mod=1e9+7; ll f[N][N]; ll tmp[N]; ll jie[1000000+5],inv[1000000+5]; int qm(int x,int y){ int ret=1; while(y){ if(y&1) ret=(ll)ret*x%mod; x=(ll)x*x%mod; y>>=1; } return ret; } int n,k; int ch[N][2],sz[N],fa[N],h[N]; int sta[N],top; int a[N]; int build(){ top=0; int las=0; for(reg i=1;i<=n;++i){ las=0; while(top&&a[i]<a[sta[top]]){ las=sta[top]; --top; if(top&&a[sta[top]]>a[i]) ch[sta[top]][1]=las,fa[las]=sta[top]; else ch[i][0]=las,fa[las]=i; } sta[++top]=i; } while(top>1) ch[sta[top-1]][1]=sta[top],fa[sta[top]]=sta[top-1],--top; return sta[1]; } int C(int n,int m){ if(n<0||m<0||n<m) return 0; return (ll)jie[n]*inv[m]%mod*inv[n-m]%mod; } void dfs(int x){ // cout<<" x ff "<<x<<" "<<ff<<endl; f[x][0]=1; if(!x) return; sz[x]=1; dfs(ch[x][0]);dfs(ch[x][1]); sz[x]+=sz[ch[x][0]]+sz[ch[x][1]]; h[x]=a[x]-a[fa[x]]; f[x][0]=1; for(reg s=0;s<=1;++s){ if(!ch[x][s]) continue; int y=ch[x][s]; for(reg j=k;j>=0;--j){ for(reg t=1;t<=j;++t){ f[x][j]=(f[x][j]+f[x][j-t]*f[y][t])%mod; } } } for(reg i=k;i>=0;--i){ for(reg j=1;j<=min(min(i,sz[x]),h[x]);++j){ f[x][i]=(f[x][i]+f[x][i-j]*C(h[x],j)%mod*C(sz[x]-(i-j),j)%mod*jie[j]%mod)%mod; } } } int main(){ rd(n);rd(k); int m=0; for(reg i=1;i<=n;++i) rd(a[i]),m=max(m,a[i]); m=max(m,max(n,k)); jie[0]=1; for(reg i=1;i<=m;++i) jie[i]=(ll)jie[i-1]*i%mod; inv[m]=qm(jie[m],mod-2); for(reg i=m-1;i>=0;--i) inv[i]=(ll)inv[i+1]*(i+1)%mod; int rt=build(); // cout<<" rt "<<rt<<endl; f[0][0]=1; dfs(rt); printf("%lld",f[rt][k]); return 0; } } signed main(){ // freopen("data.in","r",stdin); // freopen("my.out","w",stdout); Miracle::main(); return 0; }
总结:
建出笛卡尔树后有优秀的子问题性质
当前矩形的填法可以归为:先找到几行几列变成子正方形,L行L列的正方形的填法就是L!