[POI2007]堆积木Klo

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 530  Solved: 172
[Submit][Status]

Description

Mary在她的生日礼物中有一些积木。那些积木都是相同大小的立方体。每个积木上面都有一个数。Mary用他的所有积木垒了一个高塔。妈妈告诉Mary游戏的目的是建一个塔，使得最多的积木在正确的位置。一个上面写有数i的积木的正确位置是这个塔从下往上数第i个位置。Mary决定从现有的高塔中移走一些，使得有最多的积木在正确的位置。请你告诉Mary她应该移走哪些积木。

Input

输入文件的第一行为一个数n，表示高塔的初始高度。第二行包含n个数a1,a2,...,an，表示从下到上每个积木上面的数。(1<=n<=100000,1<=ai<=1000000)。

Output

注意：请输出最多有多少点可以处在正确位置

Sample Input

5
1 1 2 5 4

Sample Output

3

HINT

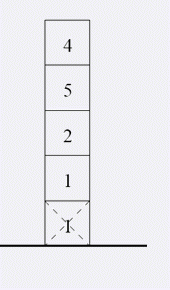
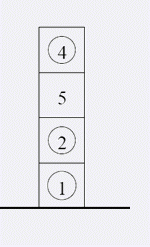
 题解：

摘自：

BZOJ1109: [POI2007]堆积木Klo

先列下DP方程。令f[i]是第i个积木在自己的位置上时，前i个积木中最多能归位的数目。

f[i]=max{f[j]|i>j,a[i]>a[j],a[i]-a[j]<=i-j}+1

(无后效性和最优子结构都是可以保证的。统计答案的时候，每个f[]取一个mx）

其中a[i]>a[j]是保证i,j都在自己的位置上，a[i]-a[j]<=i-j是为了保证中间有足够的积木让i能在a[i]这个位置上。

为了让每个限制只和位置有关，a[i]-a[j]<=i-j可以变形为a[i]-i<=a[j]-j。

1：a[i]-i<=a[j]-j ===> -a[i]+i>=-a[j]+j

2：                                  a[i]>a[j]

得到i>j……说明只要满足a[i]>a[j]和a[i]-i<=a[j]-j，则一定满足i>j！

那么就只要按照a[i]-i排序（你想按照a[i]排序也行，那样两数相等就在求LIS的时候判了），求LIS即可。

由于a[i]-i相等时，a[i]升序就可以使答案最大化，所以排序的时候第二关键字要弄成a[i]。

（我们现在只要满足两个条件：

a[i]>a[j]

i-a[i]>=j-a[j]

在排好序的新数列中，最后的LIS就是最后剩下的归位的积木。

首先这样的选法肯定是合法的。因为下标和数值，可以满足这两个条件

并且这样肯定是最优的，对于每一个位置，会求一个前i位LIS，是最长的一个，并且，LIS的方程，f[i]=max(f[j],a[j]<a[i],j<i)+1

就满足了原来的DP方程。相当于从所有的合法转移中，选择了一个最大的。

实际上，LIS里的f数组，和我们开始的DP中的f数组，是同一个数组。本质意义是一样的。

因为，转移的条件一样，转移的方程也一样。

所以，两个f一样。

所以，这个变形是等价的。

）

代码：

（网上借鉴）

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 100100
#define M 1000100
using namespace std;
struct node
{
    int x,y;
    friend bool operator < (node a,node b)
    {
        if(a.x==b.x)return a.y<b.y;
        return a.x<b.x;
    }
}b[N];
int d[M],a[N];
int n,ma,tot;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        if(i-a[i]<0)continue;
        b[++tot].x=i-a[i],b[tot].y=a[i];
    }
    sort(b+1,b+tot+1);
    memset(d,0x3f,sizeof(d)); 
    for(int i=1;i<=tot;i++)
    {
        int l=1,r=ma,ans=0;
        while(l<=r)
        {
            int mid=(l+r)>>1;
            if(b[i].y>d[mid])ans=mid,l=mid+1;
            else r=mid-1;
        }
        ma=max(ma,ans+1);
        d[ans+1]=min(d[ans+1],b[i].y);
    }
    printf("%d
",ma);
}