参考&&推荐:
LCT总结——概念篇+洛谷P3690[模板]Link Cut Tree(动态树)(LCT,Splay)
[Link-Cut-Tree]【学习笔记】
一、概括
一种支持维护树的森林的算法。
采用实链剖分,多棵splay维护每个实链,键值就是节点的深度。
即,中序遍历就是这个链从上到下的节点组成。
同一个原树上的splay之间也连接,但是不同的实链的splay之间的父子边单向,由儿子指向父亲。
即,认父不认子。
也就是说,一个节点可以成为多个节点的父亲,但是最多只认一个左儿子,一个右儿子。
可以支持,
1.加入一条边(连接两棵树),
2.删除一条边
3.处理一条路径上的询问。
二、核心思想
1.实链剖分
区别于重链剖分和长链剖分,实链剖分的实链是动态的。
即,轻儿子重儿子随便换。根据需求会换不同的儿子。
2.原树和辅助树分开处理。
辅助树即splay(森林)
一棵原树可以认为是一棵部分联通的splay,也可以看做是多个splay,之间认父不认子
(以下称维护一条链的splay叫小splay,整个原树的splay叫大splay)
原树和辅助树没有区分开是初学者懵逼的一大原因。
splay的中序遍历就是这个链从上到下的节点组成。
可以参考上面第二篇博客。
3.每次提取一条完整的链进行处理。两端就是路径的起始终止节点。
“两端就是路径的起始终止节点。”这句话尤为关键。
makert之后access之后splay就可以把一个链放进一个子树里,轻松查找。(类似于普通splay区间查询)
还有一些性质,可以参考第一篇博客。
1.深度为键值,严格递增(显然,splay不可能存在两个点键值相同)
2.每个点属于一个小splay
3.认父不认子。最多一个重儿子
三、函数
1.access(灵魂函数)
access意为进入,接近。
就是打通一条root到x的路径。把root到x的路径变成实链。
无关的边都变成轻链。
摘自:LCT总结——概念篇+洛谷P3690[模板]Link Cut Tree(动态树)(LCT,Splay)
A是树根,access(N)
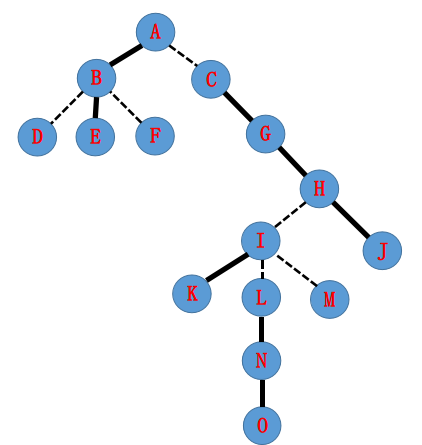
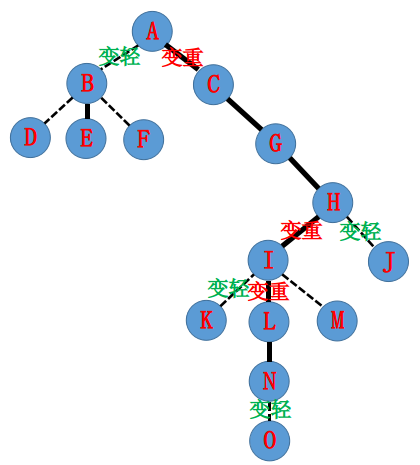
这里我们直接把轻边变成重边。
void access(int x){
for(int y=0;x;y=x,x=t[x].fa){
splay(x);t[x].ch[1]=y;pushup(x);
}
}
开始扔掉右儿子,就是扔掉N-O这块子树。
发现一个关键的性质,
这样,N和A在同一个小splay里面,N和A的路径上的点就是这个splay中的所有点。
2.splay(灵魂函数)&&rotate&&nrt
注意:这里splay仅在小splay中进行。都是把x转到这个小splay的根。
与一般splay不同的是,
LCT中splay的节点编号就是原树节点编号。可以随机访问。没有kth这一步
也就意味着,pushdown必须跟上。
用一个栈记录父亲,然后依次pushdown
之后像原来一样splay即可。
void splay(int x){
int y=x,z=0;
sta[++z]=y;
while(nrt(y)) y=t[y].fa,sta[++z]=y;
while(z) pushdown(sta[z--]);
while(nrt(x)){
y=t[x].fa,z=t[y].fa;
if(nrt(y)){
rotate((t[y].ch[0]==x)==(t[z].ch[0]==y)?y:x);
}
rotate(x);
}
pushup(x);
}
值得注意的是,由于不能转出去,所以必须有一个nrt(not root)判断是否x是当前小splay的根。
通过father认不认这个x儿子判断是否为根。
否,返回1,是,返回0
bool nrt(int x){
return (t[t[x].fa].ch[0]==x)||(t[t[x].fa].ch[1]==x);
}
由于认父不认子,所以小splay的根的father不能设置儿子关系。
void rotate(int x){
int y=t[x].fa,d=t[y].ch[1]==x;
t[t[y].ch[d]=t[x].ch[!d]].fa=y;
if(nrt(y)) t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x;//nrt注意
else t[x].fa=t[y].fa;//无论如何要设置x的fa
t[t[x].ch[!d]=y].fa=x;
pushup(y);
}
3.makert&&reverse(灵魂函数)
由于深度单调递增,所以实链一定是竖直往下的。
对于x到y的路径,x,y可能不在一个实链上。
原树是一棵无根树,所以可以随时换根。
引入makert函数,把x钦定成为原树的根。
只要调整中序遍历即可。
access(x),splay(x),然后reverse(x),那么,就相当于直接翻转。
那么,本来x是和root相连的实链的底端,这样reverse一下,直接变成了根!!
神奇操作。
void rev(int x){
ls^=rs^=ls^=rs;
t[x].r^=1;
}
void makert(int x){
access(x);
splay(x);
rev(x);
}
makert和access结合,就可以处理路径问题了。(见split)
4.findrt
查找一个点所在的原树的根。
找中序遍历第一个即可。
int findrt(int x){
access(x);splay(x);
while(t[x].ch[0]) x=t[x].ch[0];
return x;
}
值得注意的是,原树的根现在不是所属小splay的根了,根变成了x
5.split
提出x到y的路径。
根据access的得出的性质可以发现,makert(x),再access(y),就把x到y的路径打通了。
然后splay(y),那么这个路径就是y和y的左子树。
void split(int x,int y){
makert(x);access(y);splay(y);
}
之后可以直接查询y的信息。
6.link
连接原树中x到y
判断是否在同一个原树里。然后把x连向y一条认父亲边。
y先不认x这个儿子,必要的时候会access
void link(int x,int y){
makert(x);
if(findrt(y)==x) return;
t[x].fa=y;
pushup(y);
}
必须要makert(x),否则link完了就不是一棵树。。。
7.cut
判断是否相连 。
makert再findrt后,如果相连,y一定是x的father,x一定是y的左儿子。
如果x的father不是y,或者x有右儿子。则没有这条边。
否则断开。
void cut(int x,int y){
makert(x);
if(findrt(y)!=x||t[x].fa!=y||t[x].ch[1]) return;
t[x].fa=t[y].ch[0]=0;
pushup(y);
}
8.pushup
维护权值
void pushup(int x){if(x)t[x].s=t[rs].s^t[ls].s^t[x].v;}
9.pushdown
主要是下放reverse标记。
void pushdown(int x){
if(t[x].r){
t[x].r=0;
rev(ls);rev(rs);
}
}
模板:
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define rs t[x].ch[1]
#define ls t[x].ch[0]
using namespace std;
typedef long long ll;
il void rd(int &x){
char ch;x=0;bool fl=false;
while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
for(x=numb;isdigit(ch=getchar());x=x*10+numb);
(fl==true)&&(x=-x);
}
namespace Miracle{
const int N=3e5+5;
int n,m;
struct node{
int fa,ch[2];
int s,v;
int r;
}t[N];
int sta[N];
void pushup(int x){if(x)t[x].s=t[rs].s^t[ls].s^t[x].v;}
void rev(int x){
ls^=rs^=ls^=rs;
t[x].r^=1;
}
void pushdown(int x){
if(t[x].r){
t[x].r=0;
rev(ls);rev(rs);
}
}
bool nrt(int x){
return (t[t[x].fa].ch[0]==x)||(t[t[x].fa].ch[1]==x);
}
void rotate(int x){
int y=t[x].fa,d=t[y].ch[1]==x;
t[t[y].ch[d]=t[x].ch[!d]].fa=y;
if(nrt(y)) t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x;//nrt注意
else t[x].fa=t[y].fa;//无论如何要设置x的fa
t[t[x].ch[!d]=y].fa=x;
pushup(y);
}
void splay(int x){
int y=x,z=0;
sta[++z]=y;
while(nrt(y)) y=t[y].fa,sta[++z]=y;
while(z) pushdown(sta[z--]);
while(nrt(x)){
y=t[x].fa,z=t[y].fa;
if(nrt(y)){
rotate((t[y].ch[0]==x)==(t[z].ch[0]==y)?y:x);
}
rotate(x);
}
pushup(x);
}
void access(int x){
for(int y=0;x;y=x,x=t[x].fa){
splay(x);t[x].ch[1]=y;pushup(x);
}
}
void makert(int x){
access(x);
splay(x);
rev(x);
}
void split(int x,int y){
makert(x);access(y);splay(y);
}
int findrt(int x){
access(x);splay(x);
while(t[x].ch[0]) x=t[x].ch[0];
return x;
}
void link(int x,int y){
makert(x);
if(findrt(y)==x) return;
t[x].fa=y;
pushup(y);
}
void cut(int x,int y){
makert(x);
if(findrt(y)!=x||t[x].fa!=y||t[x].ch[1]) return;
t[x].fa=t[y].ch[0]=0;
pushup(y);
}
int main(){
scanf("%d%d",&n,&m);
for(reg i=1;i<=n;++i){
rd(t[i].v);t[i].s=t[i].v;
}
int op,x,y;
while(m--){
rd(op);
rd(x);rd(y);
switch(op){
case 0:split(x,y);printf("%d
",t[y].s);break;
case 1:link(x,y);break;
case 2:cut(x,y);break;
case 3:splay(x);t[x].v=y;pushup(x);
}
}
return 0;
}
}
int main(){
Miracle::main();
return 0;
}
/*
Author: *Miracle*
Date: 2018/11/13 20:07:40
*/
四、比较区别&&优势所在
1.与普通平衡树
见splay函数区别。
2.树链剖分、并查集比较
支持动态加边,删边,还可以支持维护链的信息。
虽然一个logn,但是大常数还不如树剖快。
其实比树剖快
五、应用&&例题
支持的操作就是基本应用。
1.[HNOI2010]弹飞绵羊
找树根是一个麻烦点。
比较优秀的做法是,建立一个n+1的虚拟节点,所有的点都在这一棵树上,那么n+1就是永恒的根。直接LCT即可。
或者可以强行不用makert,因为序列的先后位置就是树的深度关系,所以可以利用这一点在不进行makert的情况下进行link-cut

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=200000+5; int n,m; int a[N]; struct node{ int ch[2],sz; int rev,fa; }t[N]; int sta[N]; bool nrt(int x){ return t[t[x].fa].ch[0]==x||t[t[x].fa].ch[1]==x; } void pushup(int x){ if(x) t[x].sz=t[t[x].ch[0]].sz+t[t[x].ch[1]].sz+1; } void reverse(int x){ t[x].ch[0]^=t[x].ch[1]^=t[x].ch[0]^=t[x].ch[1]; t[x].rev^=1; } void pushdown(int x){ if(t[x].rev){ reverse(t[x].ch[0]); reverse(t[x].ch[1]); t[x].rev=0; } } void rotate(int x){ int y=t[x].fa,d=t[y].ch[1]==x; t[t[y].ch[d]=t[x].ch[!d]].fa=y; if(nrt(y)) t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x; else t[x].fa=t[y].fa; t[t[x].ch[!d]=y].fa=x; pushup(y); } void splay(int x){ int y=x,z=0; sta[++z]=y; while(nrt(y)) y=t[y].fa,sta[++z]=y; while(z) pushdown(sta[z--]); while(nrt(x)){ y=t[x].fa,z=t[y].fa; if(nrt(y)){ rotate((t[y].ch[0]==x)==(t[z].ch[0]==y)?y:x); } rotate(x); } pushup(x); } void access(int x){ for(int y=0;x;y=x,x=t[x].fa){ splay(x);t[x].ch[1]=y;pushup(x); } } void link(int x,int y){ if(x>y) swap(x,y); splay(x); t[x].fa=y; } void cut(int x,int y){ if(x>y) swap(x,y); access(x);splay(y); t[x].fa=t[y].ch[1]=0; pushup(y); } void wrk(int x,int y){ if(x+a[x]<=n) cut(x,x+a[x]); if(x+y<=n) link(x,x+y); a[x]=y; } int main(){ scanf("%d",&n); for(reg i=1;i<=n;++i){ rd(a[i]); if(i+a[i]<=n) link(i,i+a[i]); } // for(reg x=1;x<=n;++x){ // cout<<x<<" : "<<t[x].fa<<" "<<t[x].sz<<" "<<t[x].ch[0]<<" "<<t[x].ch[1]<<endl; // } scanf("%d",&m); int op,x,y; while(m--){ rd(op); switch(op){ case 1:scanf("%d",&x);++x;access(x);splay(x);printf("%d ",1+t[t[x].ch[0]].sz);break; case 2:scanf("%d%d",&x,&y);++x;wrk(x,y);break; } // cout<<t[1].sz<<" "<<t[2].sz<<" "<<t[3].sz<<" "<<t[4].sz<<endl; } return 0; } } int main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/14 7:56:04 */
直接LCT维护连通性即可

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=10000+5; int n,m; struct node{ int ch[2],fa; int rev; }t[N]; int sta[N]; bool nrt(int x){ return t[t[x].fa].ch[0]==x||t[t[x].fa].ch[1]==x; } void reverse(int x){ swap(t[x].ch[0],t[x].ch[1]); t[x].rev^=1; } void pushdown(int x){ if(t[x].rev){ reverse(t[x].ch[0]); reverse(t[x].ch[1]); t[x].rev^=1; } } void rotate(int x){ int y=t[x].fa,d=t[y].ch[1]==x; t[t[y].ch[d]=t[x].ch[!d]].fa=y; if(nrt(y)) t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x; else t[x].fa=t[y].fa; t[t[x].ch[!d]=y].fa=x; } void splay(int x){ int y=x,z=0; sta[++z]=y; while(nrt(y)) y=t[y].fa,sta[++z]=y; while(z) pushdown(sta[z--]); while(nrt(x)){ y=t[x].fa,z=t[y].fa; if(nrt(y)){ rotate((t[y].ch[0]==x)==(t[z].ch[0]==y)?y:x); } rotate(x); } } void access(int x){ for(reg y=0;x;y=x,x=t[x].fa){ splay(x);t[x].ch[1]=y; } } void makert(int x){ access(x);splay(x);reverse(x); } int findrt(int x){ access(x);splay(x); // cout<<" ls "<<t[x].ch[0]<<endl; while(t[x].ch[0]) x=t[x].ch[0]; return x; } void link(int x,int y){ //cout<<" linking "<<endl; makert(x);//warning!!! t[x].fa=y; // cout<<" fa "<<t[x].fa<<endl; } void cut(int x,int y){ makert(x);access(y);splay(y); t[x].fa=t[y].ch[0]=0; } int main(){ rd(n);rd(m); char ch[233];int x,y; while(m--){ scanf("%s",ch+1); rd(x);rd(y); switch(ch[1]){ case 'Q':puts(findrt(x)==findrt(y)?"Yes":"No");break; case 'C':link(x,y);break; case 'D':cut(x,y);break; } //cout<<" rt "<<findrt(123)<<" "<<findrt(127)<<" "<<t[123].fa<<" "<<t[127].fa<<endl; } return 0; } } int main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/14 9:05:36 */
翻译一下,就是动态最小生成树。
边不好处理。
那就把边变成点。
边的权值就是点的权值。原来的真实点权值为-1
这样,splay一条链上的点最大值就是花费时间。
正着删边不好维护。时光倒流,倒着加边。
加入一条边,如果当前x,y不连通,并且(x,y)路径上存在一个边(点),权值比当前边(点)权值大,那么就切掉这个点的两个连边。
然后link上。
所以节点维护mx,子树最大权值。is,最大权值的点的编号。
cut的时候,把这个最大权值的点的编号id ,splay到根,易证只有左右儿子这两个儿子认它。(不存在更多的儿子)
直接砍断即可。
link的时候,分别link上。
注意数组别开小!!点数是N+M
(本代码cut函数没用)

#include<bits/stdc++.h> #define reg register int #define il inline #define ls t[x].ch[0] #define rs t[x].ch[1] #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=1000+5; const int M=100000+5; int n,m,q; struct node{ int fa,ch[2],mx,is,val; bool r; }t[N+M]; int sta[N+M]; struct question{ int typ,x,y; int ans; }que[N+M]; int v[N][N]; bool kil[N][N]; bool nrt(int x){ return t[t[x].fa].ch[0]==x||t[t[x].fa].ch[1]==x; } void pushup(int x){ if(t[x].val>max(t[ls].mx,t[rs].mx)){ t[x].mx=t[x].val; t[x].is=x; } else{ if(t[ls].mx>t[rs].mx){ t[x].mx=t[ls].mx; t[x].is=t[ls].is; } else{ t[x].mx=t[rs].mx; t[x].is=t[rs].is; } } } void rev(int x){ ls^=rs^=ls^=rs; t[x].r^=1; } void pushdown(int x){ if(t[x].r){ rev(ls);rev(rs); t[x].r=0; } } void rotate(int x){ int y=t[x].fa,d=t[y].ch[1]==x; t[t[y].ch[d]=t[x].ch[!d]].fa=y; if(nrt(y)) t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x; else t[x].fa=t[y].fa; t[t[x].ch[!d]=y].fa=x; pushup(y); } void splay(int x){ int y=x,z=0; sta[++z]=y; while(nrt(y)) y=t[y].fa,sta[++z]=y; while(z) pushdown(sta[z--]); while(nrt(x)){ y=t[x].fa,z=t[y].fa; if(nrt(y)){ rotate((t[y].ch[0]==x)==(t[z].ch[0]==y)?y:x); } rotate(x); } pushup(x); } void access(int x){ for(reg y=0;x;y=x,x=t[x].fa){ splay(x);t[x].ch[1]=y;pushup(x); } } void makert(int x){ access(x);splay(x);rev(x); } void split(int x,int y){ makert(x);access(y);splay(y); } int findrt(int x){ access(x);splay(x); while(t[x].ch[0]) x=t[x].ch[0]; return x; } void link(int x,int y){ makert(x); t[x].fa=y; pushup(y); } void cut(int x,int y){ split(x,y); t[x].fa=t[y].ch[0]=0; pushup(y); } void wrk(int x,int y,int z){//x----y(x--z--y) makert(x); if(findrt(y)!=x){ link(x,z);link(z,y); } else{ split(x,y); if(t[y].mx>t[z].val){ int id=t[y].is; splay(id); t[t[id].ch[0]].fa=t[t[id].ch[1]].fa=0; link(x,z);link(z,y); } } } int main(){ rd(n);rd(m);rd(q); int x=0,y=0,z=0; memset(v,-1,sizeof v); for(reg i=1;i<=m;++i){ rd(x);rd(y);rd(z); v[x][y]=v[y][x]=z; } t[0].val=-1; for(reg i=1;i<=n;++i) t[i].val=-1;//warning!!! int op; for(reg i=1;i<=q;++i){ rd(op);rd(x);rd(y); if(op==2) kil[x][y]=kil[y][x]=1; que[i].x=x,que[i].typ=op; que[i].y=y; } int tot=n; for(reg i=1;i<=n;++i){ for(reg j=i+1;j<=n;++j){ if(v[i][j]!=-1&&!kil[i][j]){ ++tot; t[tot].val=v[i][j]; wrk(i,j,tot); } } } //cout<<tot<<endl; for(reg i=q;i>=1;--i){ if(que[i].typ==1){ split(que[i].x,que[i].y); que[i].ans=t[que[i].y].mx; } else{ ++tot; t[tot].val=v[que[i].x][que[i].y]; wrk(que[i].x,que[i].y,tot); } } for(reg i=1;i<=q;++i){ if(que[i].typ==1) printf("%d ",que[i].ans); } return 0; } } int main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/14 10:30:34 */
六、总结和理解
为什么要建这么多棵辅助树?因为直接一棵树,deep键值相同,又不能合并。
所以必须多棵辅助树。但是一个点只能有两个儿子。所以就建立单向边。
但是还要支持必要时候的访问。
实链剖分的access就自底向上打通了一条链。直接可以访问。
链上有相同深度的点,不能在同一个实链上,但是必须要拉出来。
发现但是如果以一端为根,那么必然深度就不会相同了。
所以makert的随时换根,使得求路径变得十分简单。划分明确。
(至于弹飞绵羊为什么不用makert也可以,因为所有的路径都是自上而下的,本身就具备了深度不同的性质。)
所有的操作都是基于splay树高logn的性质。
所以所有操作的复杂度均摊logn(当然常数不能再大了)
