【luogu P2731 骑马修栅栏】 题解

题目链接：https://www.luogu.org/problemnew/show/P2731

这个题是欧拉回路的模板题，那么在这里给出一个hierholzer的做法。

对于求欧拉回路的问题，有Fluery算法和Hierholzers算法，两种算法。

后面一种算法无论是编程复杂度还是时间复杂度好像都比前种算法复杂度更优，但前者的应用广泛性好像比后者更高。

对于Hierholzers算法，前提是假设图G存在欧拉回路，即有向图任意点的出度和入度相同。从任意一个起始点v开始遍历，直到再次到达点v，即寻找一个环，这会保证一定可以到达点v，因为遍历到任意一个点u，由于其出度和入度相同，故u一定存在一条出边，所以一定可以到达v。将此环定义为C，如果环C中存在某个点x，其有出边不在环中，则继续以此点x开始遍历寻找环C’，将环C、C’连接起来也是一个大环，如此往复，直到图G中所有的边均已经添加到环中。

举个例子

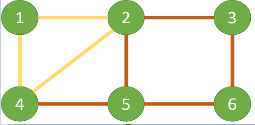
在手动寻找欧拉路的时候，我们从点 4 开始，一笔划到达了点 5，形成路径 4-5-2-3-6-5。此时我们把这条路径去掉，则剩下三条边，2-4-1-2 可以一笔画出。

这两条路径在点 2 有交接处（其实点 4 也是一样的）。那么我们可以在一笔画出红色轨迹到达点 2 的时候，一笔画出黄色轨迹，再回到点 2，把剩下的红色轨迹画完。

既然是模板题..那么当然选择好写的

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <stack>
using namespace std;
const int maxn = 1031;
int G[maxn][maxn], du[maxn];
int n,m;
stack<int> S;//用栈记录路径
void dfs(int u)//dfs过程中不需要恢复，用栈记录路径
{
    for(int v=1; v<=n; v++)
        if(G[u][v])
        {
            G[u][v]--;
            G[v][u]--;
            dfs(v);    
        }
    S.push(u);
}
int main(){
   
    cin>>m;
    int u,v;
    for(int i=1; i<=m; i++){
        cin>>u>>v;
        n = max(n,u);
        n = max(n,v); //取出点数
        G[u][v]++;
        G[v][u]++;
        du[u]++;
        du[v]++;
    }
    int s = 1;
    for(int i=1; i<=n; i++)
        if(du[i]%2==1) 
        {    
            s=i;
            break;
        }//选取起点
    dfs(s);
    while(!S.empty()){
        cout<<S.top()<<endl;
        S.pop();
    }
    return 0;
}