最近公共祖先(Lowest Common Ancestors):
简称LCA(并不是某轻型战斗机)
一.何为最近公共祖先
对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。(摘自百度百科)
那么举个简单的例子:看图
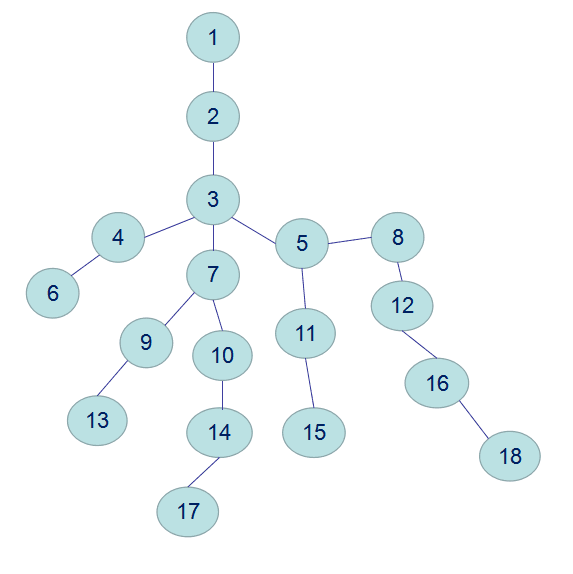
那么比如14和18的lca就是3 11和16的lca就是5
对于求lca,有很多种方法:tarjan啦,树剖啦,倍增啦,暴力......
二.如何求最近公共祖先呢
首先我们想到了:暴力大法好
对于所求的两个点,调整到同一个深度,然后一起向上跳,这样所求到的第一个相同的点就是这两个点的lca。
可是暴力肯定会T...那么怎么办呢
我们想到了之前学过的st表,利用倍增的思想来完成lca的查询。
接着我们想到了:倍增大法好
1.首先我们准备好要用到的变量
所有点的2^j层的父亲,用fa数组保存,对于fa[i][j]表示编号为i的点向上跳2^j步的父亲。maxlog用来枚举j。
head,edge,cnt邻接表的标配,不用多说。deep[i]表示i的深度,root为所给定的根节点编号。add为向树中添加一条边。
1 const int maxlog = 20; 2 const int maxn = 550000; 3 int n, m, s; 4 int root; 5 int fa[maxn][maxlog]; 6 int deep[maxn]; 7 int head[maxn]; 8 int cnt; 9 struct Edge{ 10 int next; 11 int to; 12 }e[2*maxn]; 13 void add(int u, int v) 14 { 15 e[cnt].to = v; 16 e[cnt].next = head[u]; 17 head[u] = cnt++; 18 }
2.初始化建树,预处理每个点的fa数组
dfs建树,ini初始化fa数组。
1 void dfs(int u, int p, int d) 2 { 3 fa[u][0] = p; 4 deep[u] = d; 5 for(int i = head[u]; i != -1; i = e[i].next) 6 if(e[i].to != p) dfs(e[i].to, u, d+1); 7 } 8 void init() 9 { 10 dfs (root, -1, 0); 11 for(int k = 0; k + 1 < maxlog; k++) 12 { 13 for(int v = 1; v <= n; v++) 14 if(fa[v][k] < 0) fa[v][k+1] = -1; 15 else fa[v][k+1] = fa[fa[v][k]][k]; 16 } 17 }
3.接下来就是关于倍增lca的精髓所在:
(划重点!)我们对于每一个点,还是先移动到同一高度,再开始跳。
对于第一个for便是移动到相同深度。
对于两个已经跳到了相同深度的两个点,我们从最高处向下跳,直到遇见一个两个点fa都不相同的点,即他们的lca下面的两个点。再求出这个两个点的向上跳一步的父节点。即lca。
1 int lca(int u, int v) 2 { 3 if(deep[u] > deep[v]) swap(u, v); 4 for(int k = 0; k < maxlog; k++) 5 { 6 if(deep[v] == deep[u]) break; 7 if((deep[v] - deep[u]) >> k & 1) 8 { 9 v = fa[v][k]; 10 //cout<<deep[v]<<" "<<deep[u]<<endl; 11 }//向上跳到同样深度 12 } 13 14 if(u == v) return u; 15 16 for(int k = maxlog - 1; k >= 0; k--) 17 { 18 if(fa[v][k] != fa[u][k]) 19 { 20 u = fa[u][k]; 21 v = fa[v][k]; 22 //cout<<u<<" "<<v<<endl; 23 } 24 25 }//从大向小跳下去 , 第一个遇到的不同的 26 return fa[u][0]; 27 }
模板:
https://www.luogu.org/problemnew/show/P3379
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 #include <cstring> 5 using namespace std; 6 const int maxlog = 20; 7 const int maxn = 550000; 8 int n, m, s; 9 int root; 10 int fa[maxn][maxlog]; 11 int deep[maxn]; 12 int head[maxn]; 13 int cnt; 14 struct Edge{ 15 int next; 16 int to; 17 }e[2*maxn]; 18 void add(int u, int v) 19 { 20 e[cnt].to = v; 21 e[cnt].next = head[u]; 22 head[u] = cnt++; 23 } 24 void dfs(int u, int p, int d) 25 { 26 fa[u][0] = p; 27 deep[u] = d; 28 for(int i = head[u]; i != -1; i = e[i].next) 29 if(e[i].to != p) dfs(e[i].to, u, d+1); 30 } 31 void init() 32 { 33 dfs (root, -1, 0); 34 for(int k = 0; k + 1 < maxlog; k++) 35 { 36 for(int v = 1; v <= n; v++) 37 if(fa[v][k] < 0) fa[v][k+1] = -1; 38 else fa[v][k+1] = fa[fa[v][k]][k]; 39 } 40 } 41 int lca(int u, int v) 42 { 43 if(deep[u] > deep[v]) swap(u, v); 44 for(int k = 0; k < maxlog; k++) 45 { 46 if(deep[v] == deep[u]) break; 47 if((deep[v] - deep[u]) >> k & 1) 48 { 49 v = fa[v][k]; 50 //cout<<deep[v]<<" "<<deep[u]<<endl; 51 } 52 } 53 54 if(u == v) return u; 55 56 for(int k = maxlog - 1; k >= 0; k--) 57 { 58 if(fa[v][k] != fa[u][k]) 59 { 60 u = fa[u][k]; 61 v = fa[v][k]; 62 } 63 } 64 return fa[u][0]; 65 } 66 int main() 67 { 68 memset(head,-1,sizeof(head)); 69 int a,b; 70 scanf("%d%d%d",&n,&m,&root); 71 for(int i = 1; i < n; i++) 72 { 73 scanf("%d%d",&a,&b); 74 add(a,b); 75 add(b,a); 76 } 77 init(); 78 for(int i = 1; i <= m; i++) 79 { 80 int u,v,a; 81 scanf("%d%d",&u,&v); 82 a = lca(u,v); 83 printf("%d ",a); 84 } 85 return 0; 86 }
