树状数组(Binary Indexed Tree(B.I.T))
是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只
能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。-------摘自百度百科
对于树状数组这种数据结构,关键词一是树状,另一个则是数组。
请看下图:
我们令每个叶节点代表每一个元素。
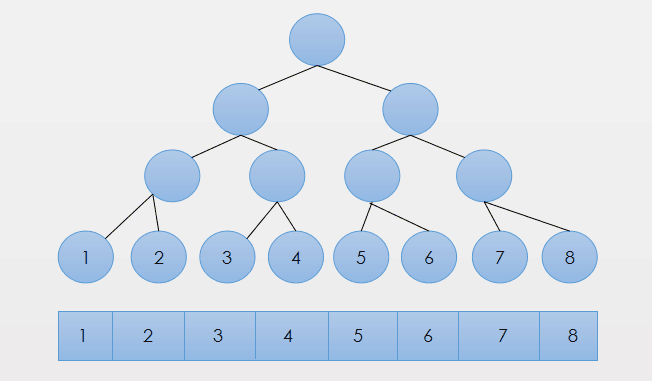
现在我们变形一下,顺便加上数组的编号:
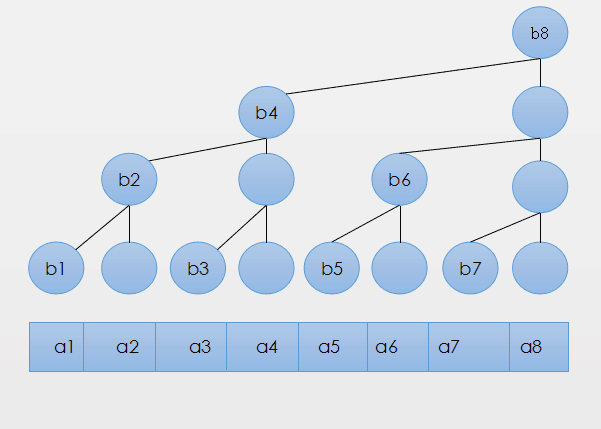
a数组是原数据。
b数组的节点,代表其所有子节点之和。
b[1] = a[1]
b[2] = a[1] + a[2]
b[3] = a[3]
b[4] = a[1] + a[2] + a[3] + a[4]
b[5] = a[5]
b[6] = a[5] + a[6]
b[7] = a[7]
b[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8]
这时,我们再把b数组转化成二进制编码:
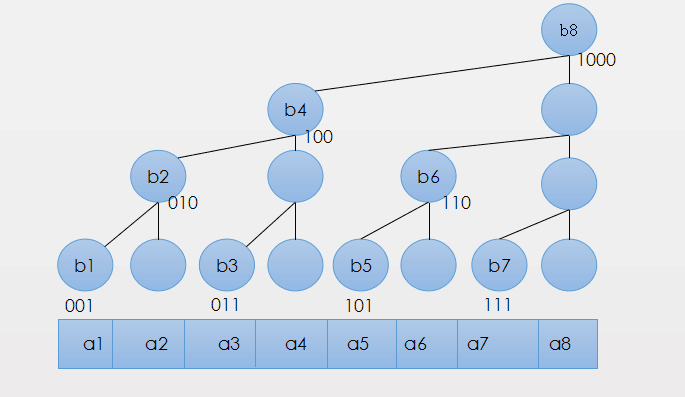
可以发现:
1 int lowbit(int x) 2 { 3 return x&(-x); 4 }
其实......很短......背吧......
接着是修改函数:
1 void add(int k, int num) 2 { 3 while(k<=n) 4 { 5 BIT[k]+=num; 6 k += lowbit(k); 7 } 8 }
BIT就是b数组
在位置k上加上num,我们用lowbit枚举出与k有关的位置,依次加上num。
举个栗子:
比如我们要修改1位置的值。与之有关的是b[1] b[2] b[4] b[8]。
第一次 k = 1,BIT[1] += num后,lowbit(1) = 1,k+=1;
第二次 k = 2,BIT[2] += num后,lowbit(2) = 2,k+=2;
第三次 k = 4,BIT[4] += num后,lowbit(4) = 4,k+=4;
第四次 k = 8,BIT[8] += num后,lowbit(8) = 8;
another:
修改3位置的值。与之有关的是b[3] b[4] b[8]。
第一次 k = 3,BIT[3] += num后,lowbit(3) = 1,k+=1;
第二次 k = 4,BIT[4] += num后,lowbit(4) = 4,k+=4;
第三次 k = 8,BIT[8] +=num后, lowbit(8) = 8;
最后是查询操作:
在这里,我们反着来做
1 int query(int k) 2 { 3 int sum = 0; 4 while(k>0) 5 { 6 sum+=BIT[k]; 7 k-=lowbit(k); 8 } 9 return sum; 10 }
跟修改的原理是一样的,不过是反着做,比如查询7位置之前所有的和,就是BIT[7] + BIT[6] + BIT[4]。
这里你会想,我们的查询函数是查询从 1——k 的值的和,要是查询一个区间 l——r(包含 l 和 r 的值) 的话怎么办?
我们利用前缀和的思想,查询 l——r 就等于query(r) - query(l-1)。
所以,luogu P3374 树状数组的模板1,就解决啦~
https://www.luogu.org/problemnew/show/P3374
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 int n,m; 6 int BIT[500070],a[500070]; 7 int lowbit(int x) 8 { 9 return x&-x; 10 } 11 void add(int k, int num) 12 { 13 while(k<=n) 14 { 15 BIT[k]+=num; 16 k += lowbit(k); 17 } 18 } 19 int query(int k) 20 { 21 int sum = 0; 22 while(k>0) 23 { 24 sum+=BIT[k]; 25 k-=lowbit(k); 26 } 27 return sum; 28 } 29 int main() 30 { 31 scanf("%d%d",&n,&m); 32 for(int i=1;i<=n;i++) 33 { 34 scanf("%d",&a[i]); 35 add(i,a[i]);//初始化元素,当然是每个位置i加上a[i]啦 36 } 37 38 for(int i=1;i<=m;i++) 39 { 40 int c; 41 scanf("%d",&c); 42 if(c == 1) 43 { 44 int k,num; 45 scanf("%d%d",&k,&num); 46 add(k,num); 47 } 48 else 49 if(c == 2) 50 { 51 int l,r; 52 scanf("%d%d",&l,&r); 53 printf("%d ",query(r)-query(l-1)); 54 } 55 } 56 return 0; 57 }
