直接给出题目吧。。。
问题 D(1988): 【高级算法】火力网
时间限制: 1 Sec 内存限制: 128 MB
题目描述
给出一个N*N的网格,用'.'表示空地,用'X'表示墙。在网格上放碉堡,可以控制所在的行和列,但不能穿过墙。问:最多能放多少个碉堡?
输入
第1行:一个整数N(N<=20)接下来N行,每行N个字符
输出
第1行:1个整数,表示最多可放碉堡数。样例输入
4
.X..
....
XX..
....
样例输出
5
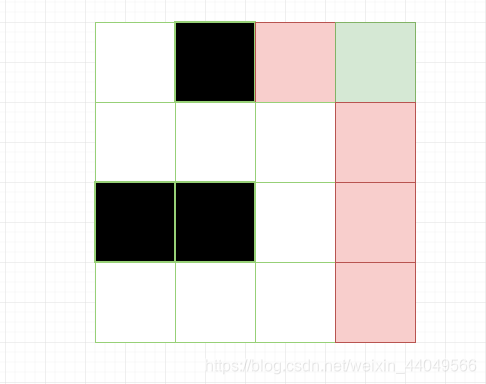
不知为何此题的图片居然莫名其妙的消失了,于是自己动手画了一张关于样例的图。
来解释一下样例吧。
现在我们要做的就是在白色格子上放上碉堡。每个碉堡都可以控制它所在的行和列,直到遇到了黑色格子。下图便是一个碉堡的攻击范围。
我们要做的便是在这个地图中放入尽量多的骑士,使他们都不能互相攻击。
题意应该说的很明显了吧,现在我们就要思考一下此题的做法。
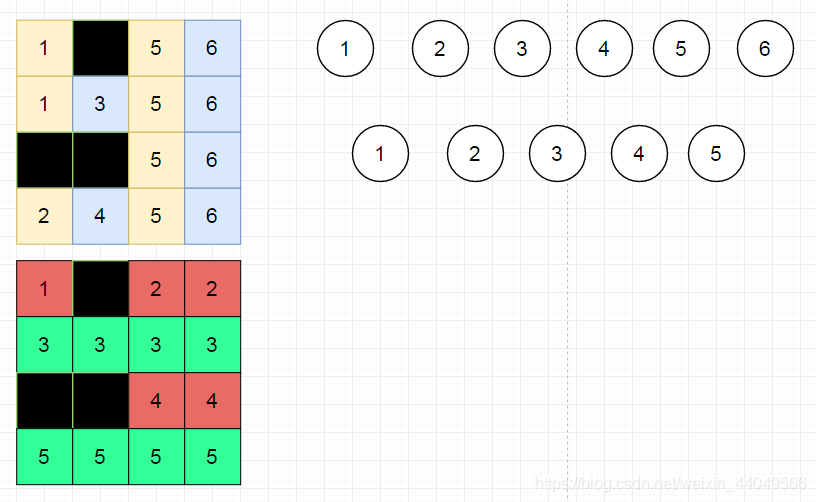
骑士的攻击有两个方向,到黑格子为止。所以我们不妨将所有的独立的横向块和独立的竖向块分为两个部,并给它们编上号。
我们可以发现如果任选两个相交的横块与竖块,在它们的交点上放上一个碉堡,则这两个块中都不能再放上碉堡了。这便符合二分图的性质。而最多的可放骑士数则是二分图的最大匹配。
于是我们的方法就出来了,将所有的横块与竖块编上号,如果它们相交便连上边。最后只需要求出最大匹配数即可。具体实现详见代码。
代码
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
#define N 50
char map[N][N];
int fuck[N][N],n,m,vis[N],match[N];
vector <int> G[N];
void Handle() {
int cnt=1;
for(int j=1;j<=n;j++) {
int flag=0;
for(int i=1;i<=n;i++) {
if(map[i][j]!='X')
fuck[i][j]=cnt,flag=0;
else if(map[i-1][j]!='X')
cnt++,flag=1;
}
cnt++;
}
m=cnt;cnt++;
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
if(map[i][j]!='X')
G[fuck[i][j]].push_back(cnt);
else if(map[i][j-1]!='X')
cnt++;
}
cnt++;
}
}
bool dfs(int u) {
for(int i=0,v;i<G[u].size();i++) {
v=G[u][i];
if(vis[v]) continue;
vis[v]=1;
if( !match[v] || dfs( match[v] )) {
match[v]=u;
return 1;
}
}
return 0;
}
int hungary() {
int ans=0;
for(int i=1;i<=m;i++) {
memset(vis,0,sizeof(vis));
if(dfs(i)) ans++;
}
return ans;
}
int main() {
cin>>n;
for(int i=1;i<=n;i++ ) for(int j=1;j<=n;j++)
cin>>map[i][j];
Handle();
/*for(int i=1;i<=m;i++) {
for(int j=0;j<G[i].size();j++)
cout<<G[i][j]<<' ';
cout<<endl;
} */
cout<<hungary();
}
最后说一句。有个奇怪的想法,如果这个地图是三维的,是不是就需要用到“三分图最大匹配”了?