向量点乘（内积）
白话：每个对应的值依次相乘然后想相加，是一个标量，也是二向量的模相乘后再乘以夹角的余弦值
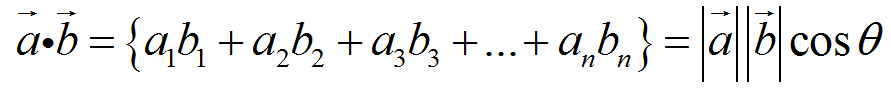
性质：如果两个向量垂直则点积为0，因为cos90°=0，反之不是，如果零向量与任何向量的点积都是0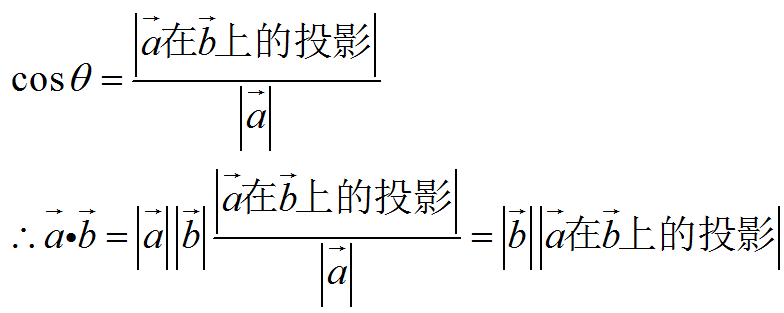
也就是说两个向量在同方向上的程度大小，换句话说，就是两个向量在相同方向上的乘积。
从cosθ上也可以看出，如果θ越小，则内积越大
也就是为什么要叫做内积的原因吧。
垂直=正交
向量叉乘（外积）
外积仅仅在R3内有用
计算方法如下：
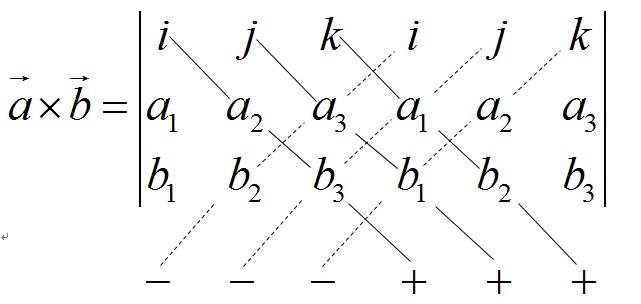
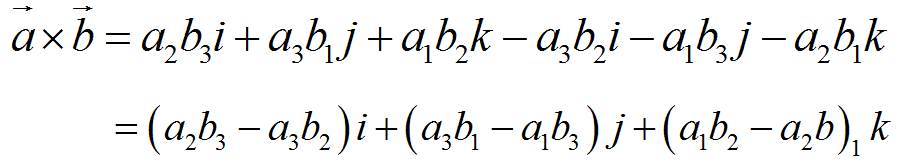
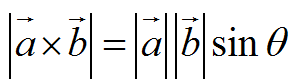
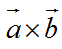是向量a和向量b所构成平面的法向量，方向符合右手定理。（三维空间）
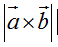是向量ab所构成四边形的面积。（二维空间）
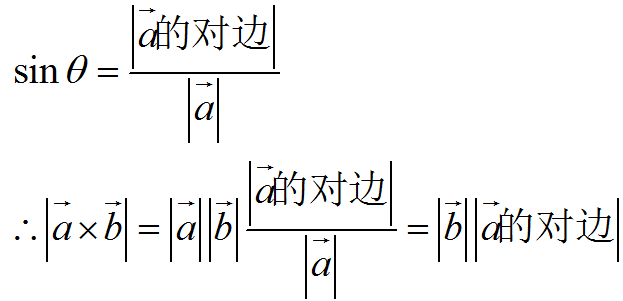
也就是说，ab的外积的模相当月b乘以a在b以外的部分（也就是垂直于b的分量），
垂直于b的分量越大，则ab的外积越大，ab的面积也就越大，因为b的长度是固定的。
所以这就是叫做外积的原因吧。
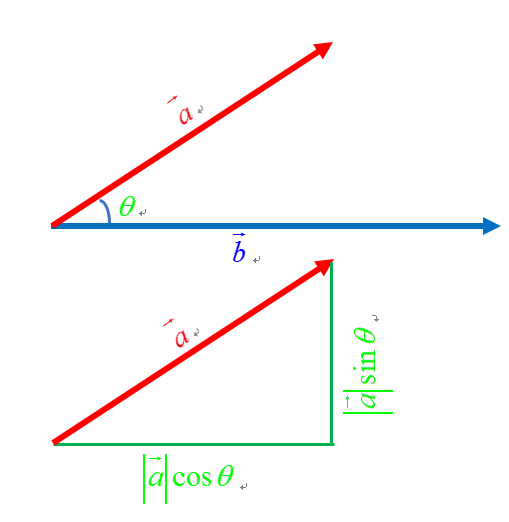
可以这么做，以b为轴做a的分量，
a落在b上的分量乘以b就是a与b的内积
a没落在b上，与b垂直的分量，乘以b就是b的外积。
内积相当于测量同向的程度，外积相当于测量垂直的程度。