问题描述
首先我们需要理解:最长公共子序列(longest common sequence)和最长公共子串(longest common substring)不是一回事儿。什么是子序列呢?即一个给定的序列的子序列,就是将给定序列中零个或多个元素去掉之后得到的结果。什么是子串呢?给定串中任意个连续的字符组成的子序列称为该串的子串。详见下图:
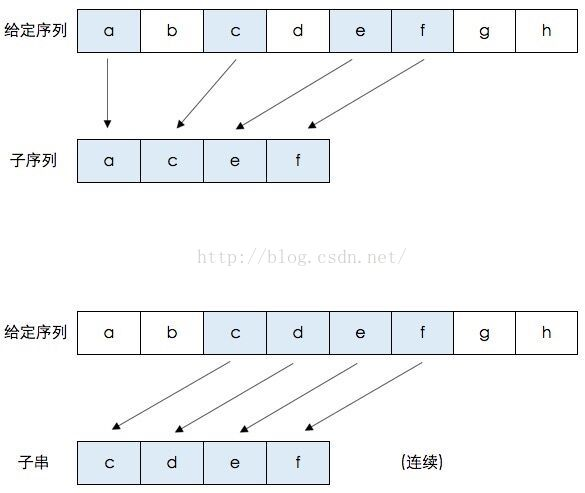
也就是说,最长公共子序列不一定连续!
而最长公共子序列问题就是:求解两个序列的最长公共子序列的长度。这里采用动态规划法和备忘录法求解。
两种方法对比:
备忘录方法
- 备忘录方法要用递归实现
- 递归是自顶向下的解决问题的:即从目标开始,将问题划分,对子问题求解,直到边界
- 递归前对备忘录进行查询,当前备忘录未被填写时,则进行递归,否则直接返回备忘录的内容(核心,提高算法效率)
- 当整个问题的求解过程中有大量子问题无需求解时,备忘录更
省时 - 一般要对备忘录进行初始化,为了之后快速判断是否有已经填写过备忘录
动态规划法
- 通过循环实现
- 递推式是自下而上解决问题的:即从边界开始,逐步对问题求解,直到抵达目标
- 当整个问题的求解过程中全部都要进行计算时,则应该使用递推式
递归公式
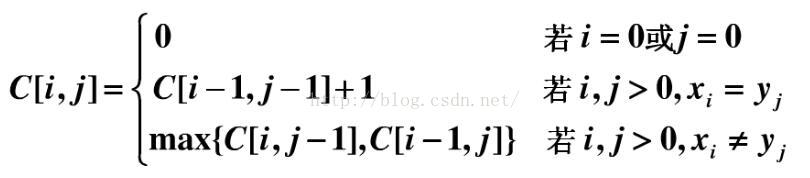
核心代码
// 动态规划
public static void f1(char arr1[],char arr2[],int n,int m) {
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(arr1[i-1]==arr2[j-1]) {
dp[i][j]=dp[i-1][j-1]+1;
}else {
dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
System.out.println(dp[n][m]);
}
// 备忘录
public static int f2(char arr1[],char arr2[],int n,int m) {
if(n==0||m==0) {
return 0;
}else if(arr1[n-1]==arr2[m-1]) {
dp[n][m]=f2(arr1,arr2,n-1,m-1)+1;
}else {
dp[n][m]=Math.max(f2(arr1,arr2,n-1,m),f2(arr1,arr2,n,m-1));}
return dp[n][m];
}
完整代码在:https://gitee.com/KSRsusu/arithmetic/tree/master/src
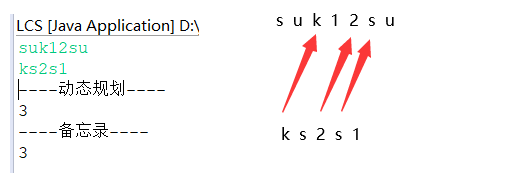
运行示例
从短的开始逐个与长的开始匹配,解析与结果如图:
参考博客