所谓的出入栈问题有两种比较常见的描述:
1、现在有若干个数,进行出入栈操作。要求不能进行非法的栈操作(也就是说栈为空的时候不能进行弹栈),现在给你一个总次数(当然我们知道这个必须是偶数),要求判断有多少种可能的序列。
2、现有若干个数目相等的+1和-1,现在要求进行操作,也就是选择不同的顺序将他们加起来,但是要保证没一个时刻式子的值都大于零,问有多少种可能的排列顺序。
看到第二个问题我们很容易会想到这是一个数学问题,而且还肯能就是个排列组合,但是试一下我们会发现不能找到这样的公式(至少我现在还没见过)。其实这个问题是一个非常简单的动态规划问题。
首先我们可以看到,没选择下一步的时候都是使式子(第一个说法中就是栈的状态,不过其实第二种是第一种的一个抽象)的值编导另一个状态,而状态的转换只有可能是两种情况。这就有点像是经典的三角数阵的问题了,只是我们这里有个值必须大于零的约束条件。于是我们只要把这个加上就行。用dp[i][j]表示前面选择了i个+1,j个-1,我们能得到方程:
dp[i][j]=dp[i-1][j]+dp[i][j+1] (i>=j)
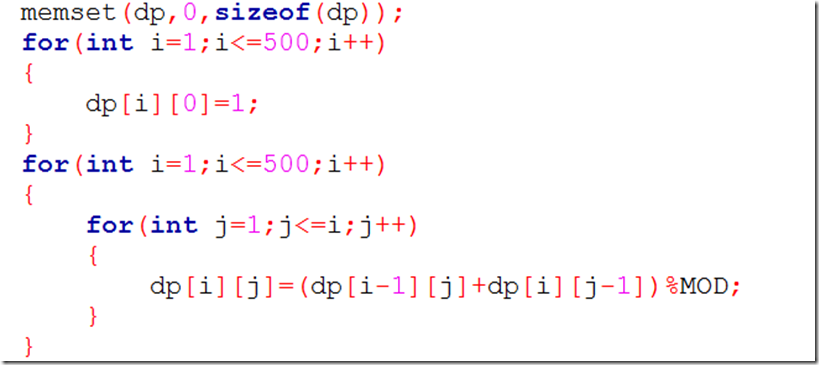
代码如下: