1263. Minimum Moves to Move a Box to Their Target Location

问题：

推箱子问题。

给定n*m二维数组:

• . -> 通路
• T -> 箱子目标位置
• B -> 箱子当前位置
• S -> 人当前位置
• # -> 障碍（墙）位置

人S去推箱子B，使得箱子到达目标位置T，箱子最少移动多少步？

Example 1:
Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#",".","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.

Example 2:
Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#","#","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: -1

Example 3:
Input: grid = [["#","#","#","#","#","#"],
               ["#","T",".",".","#","#"],
               ["#",".","#","B",".","#"],
               ["#",".",".",".",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 5
Explanation:  push the box down, left, left, up and up.

Example 4:
Input: grid = [["#","#","#","#","#","#","#"],
               ["#","S","#",".","B","T","#"],
               ["#","#","#","#","#","#","#"]]
Output: -1
 

Constraints:
m == grid.length
n == grid[i].length
1 <= m <= 20
1 <= n <= 20
grid contains only characters '.', '#',  'S' , 'T', or 'B'.
There is only one character 'S', 'B' and 'T' in the grid.

　　

example 1:

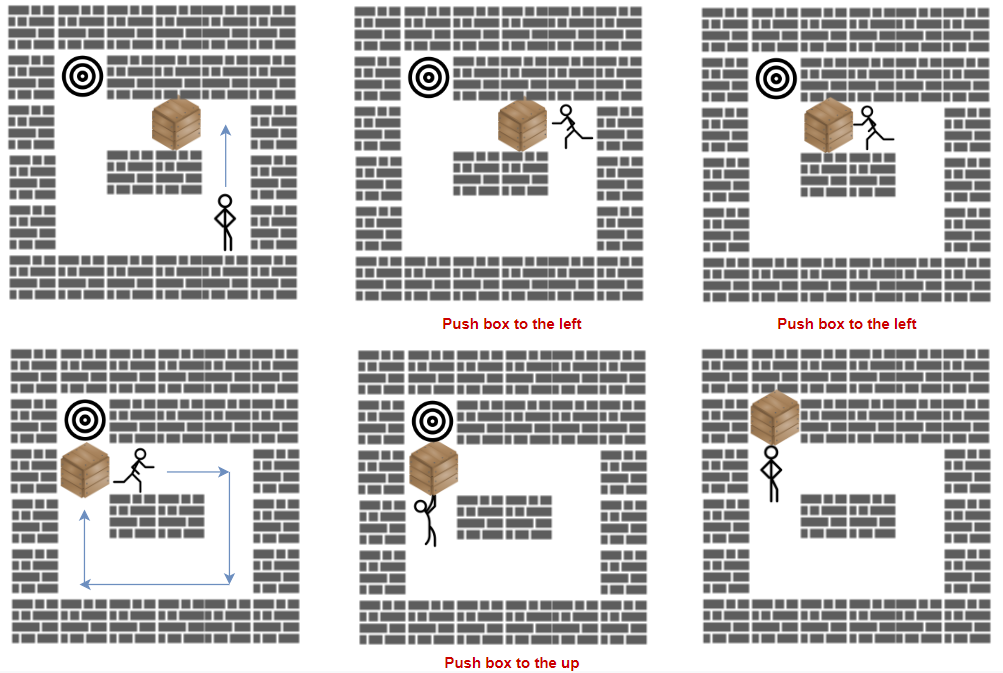
解法：BFS + priority_queue

• 状态：（保存在visited中，防止重复。）
• 人的位置
• 箱子的位置
• queue中需要信息：
  • 状态
  • 当前箱子移动了多少步
  • 决定是否先选择这个状态进行转移：权值
    • 当前箱子 距 目标 的绝对距离 + 已经移动的步数。
    • 值越小，越优先处理。

• 选择：
  • 人移动：四个方向

• 对于当前状态的处理：
  • 若当前box的位置==target的位置，返回当前步数moves。
  • 人移动4个方向：（不能出界or碰到墙）
    • 移动后，人==箱子 的位置，
      • 那么箱子被推动，向人移动的同一方向（不能出界or碰到墙）
      • 这时得到  新的人的位置np + 箱子位置nb -> 新状态，若visited中不存在，可以入队。
      • 入队内容：
        • 新状态：新的人的位置np + 箱子位置nb
        • 当前箱子移动了多少步：当前步数+1
        • 权值：新箱子nb到target的距离 + 当前步数+1
    • 移动后，人!=箱子 的位置，
      • 那么只有人移动，箱子不动
      • 这时得到 新的人的位置np + 原箱子位置box -> 新状态，若visited中不存在，可以入队。
      • 入队内容：
        • 新状态：新的人的位置np + 原箱子位置box
        • 当前箱子移动了多少步：当前步数（不变）
        • 权值：原来权值（原箱子box到target的距离 + 当前步数）（不变）

代码参考：

class cmp {
public:
    bool operator()(const array<int,4>& a, const array<int,4>& b) {
        return a[0]>b[0];//10,9,8...1 return 1
    }
};
class Solution {
public:
    //权值degree：箱子距离目标的距离dist+箱子移动过的步数
    //优先尝试上述权值较小的。->优先队列
    //状态：人的位置 & 箱子的位置
    //选择：人移动：上下左右四个方向
    int MASK = 20;//20
    int dir[5] = {1,0,-1,0,1};
    vector<int> target;
    int n,m;
    int dist(vector<int>& box) {
        return abs(box[0]-target[0]) + abs(box[1]-target[1]);
    }
    int pos(vector<int>& p) {
        return p[0]*MASK+p[1];
    }
    string toString(int a, int b) {
        return ::to_string(a)+ "_" + ::to_string(b);
    }
    int minPushBox(vector<vector<char>>& grid) {
        vector<int> box;
        vector<int> person;
        int moves = 0;
        n=grid.size();
        m=grid[0].size();
        priority_queue<array<int,4>, vector<array<int,4>>, cmp> q;
        //degree, box_moves, person, box
        //默认最大堆，less：从小到大排序，返回最后一个数(最大值) 函数体:return para_1 < para_2
        // greater:从大到小排序，返回最后一个数(最小值) 函数体:return para_1 > para_2
        unordered_set<string> visited;//person:x*20+y, box:x*20+y
        //initialize:
        for(int i=0; i<n; i++) {
            for(int j=0; j<m; j++) {
                if(grid[i][j]=='T') target={i,j};
                else if(grid[i][j]=='B') box={i,j};
                else if(grid[i][j]=='S') person={i,j};
            }
        }
        q.push({dist(box)+0, moves, pos(person), pos(box)});
        //visited.insert(toString(pos(person),pos(box)));
        //loop
        while(!q.empty()) {
            auto [cur_degree, cur_moves, pp, pb] = q.top();
            person = {pp/MASK, pp%MASK};
            box = {pb/MASK, pb%MASK};
            q.pop();
            if(box[0]==target[0] && box[1]==target[1]) return cur_moves;
            if(!visited.insert(toString(pp, pb)).second) continue;
            for(int d=1; d<5; d++) {
                vector<int> np = {person[0]+dir[d-1], person[1]+dir[d]};
                if(np[0]<0 || np[1]<0 || np[0]>=n || np[1]>=m 
                   || grid[np[0]][np[1]]=='#') continue;
                if(np[0]==box[0] && np[1]==box[1]) {//POS(person) == POS(box)
                    vector<int> nb = {box[0]+dir[d-1], box[1]+dir[d]};//box按照同样的方向移动一位
                    if(nb[0]<0 || nb[1]<0 || nb[0]>=n || nb[1]>=m 
                       || grid[nb[0]][nb[1]]=='#') continue;
                    //if(visited.insert(toString(pos(np), pos(nb))).second) {
                        q.push({dist(nb)+cur_moves+1, cur_moves+1, pos(np), pos(nb)});
                   // }
                } else {//box 不动
                    //if(visited.insert(toString(pos(np), pos(box))).second) {
                        q.push({cur_degree, cur_moves, pos(np), pos(box)});
                    //}
                }
            }
        }
        return -1;
    }
};