二分类

二分类

 分类问题是机器学习中非常重要的一个课题。现实生活中有很多实际的二分类场景，如对于借贷问题，我们会根据某个人的收入、存款、职业、年龄等因素进行分析，判断是否进行借贷；对于一封邮件，根据邮件内容判断该邮件是否属于垃圾邮件。

图1-1 分类示意图

回归作为分类的缺陷

 由于回归的输出类型是连续性，不能直接输出类别，因此通常将某个区间内的取值作为某个类别。以二分类为例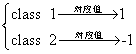，则有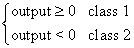。似乎可以解决分类问题，但如果出现图1-2右图情况，显然绿色的分界线具有更好的鲁棒性，但使用回归进行梯度下降时，为了减少整体误差，最终的分界线就变为紫色。

 

 

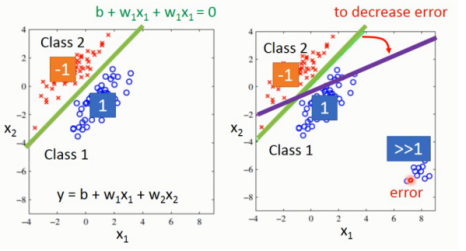
图1-2 二分类示例图

回归应用于多分类中的缺陷

 在进行回归时，需要有一个样本的标签。那么，如果我们假设class1的标签为1，class2的标签为2，class3的标签为3，那这就意味你做了一个潜在假设：class1和class2比较接近，class1跟class3比较远。但如果实际数据并不符合这个假设，使用回归就会得到一个很差的结果。

贝叶斯分类

 可以从概率的角度进行分类，分别计算出某个样本属于各个类别的概率，最后选择最大的概率作为样本的类别；假设Box1和Box2分别是两个类别，其中数据的分布如图1-3所示，当给定一个蓝色圆圈，能否求解蓝色圆圈Blue是从Box1还是Box2取出?

图1-3 盒子分类样例

 分别计算P(B₁|Blue)、P(B₂|Blue)

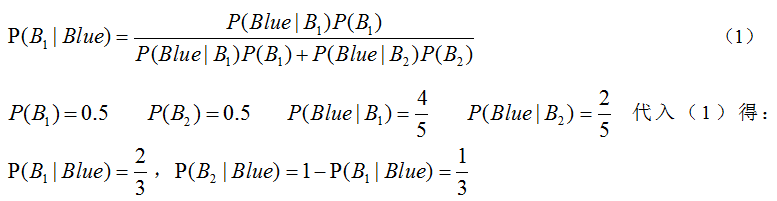
 所以，蓝色圆圈从Box1中取出的概率更大。

数据分布假设

  在计算（1）的时候，P(Blue|B₁)是比较好计算的，但是在一些更复杂的情况下，我们就很难直接统计出P(Blue|B₁)；例如，我们已知数据集{（2,1）,（3,1）,...（4,7）}是属于class1,那么当给定数据x=（5,1）,如何计算P(x|class1)？

   通常我们假设数据是由正态分布生成而来：

  

  采用极大似然估计，求解出参数；极大似然估计是在已知数据集和模型，但不知道模型的具体参数时，对参数进行求解的方法。极大似然估计做出这样一个假设：如果某组参数使已知数据集生成的概率达到最大，这组参数就是我们所要求解。以（2）为例：

   

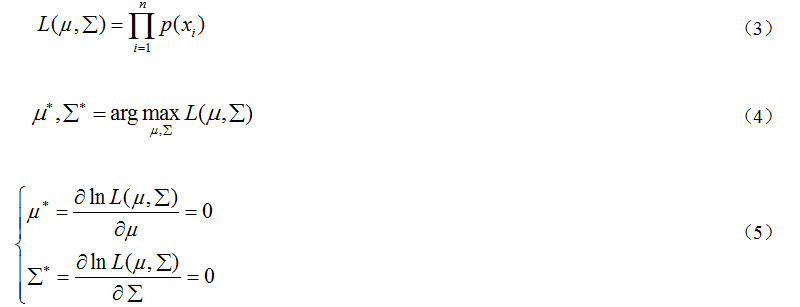
 解（5）得：

 

 将求解出的（6）带入（2）中就求解出高斯分布。对于未知数据，带入（2）便可获得P(x|class1)。

 

Logistics回归推导过程

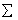  对于不同类别的数据，我们可以分别求解出，但是对于对于不同的类别可以共享。因为对于不同类别都求解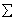，会导致模型参数过多，从而导致过拟合。因此，我们对（1）进行更一般的描述，并进行适当转化处理

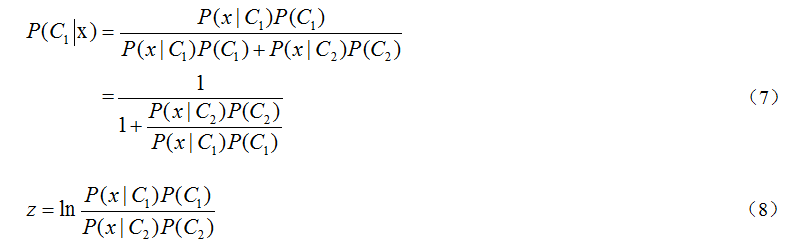
 将（8）带入（7）中有

   

 对（8）进行处理

 

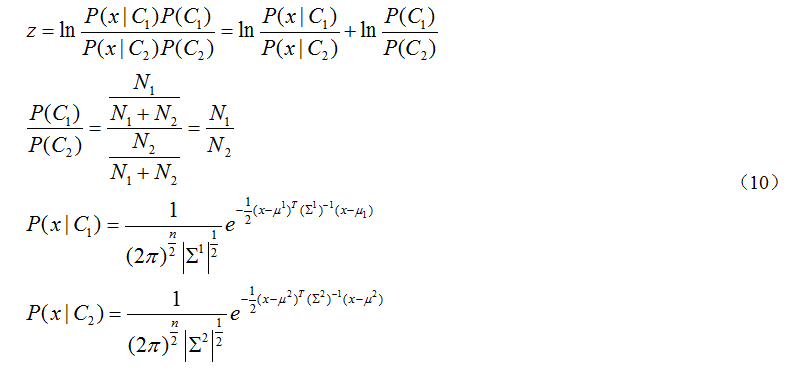
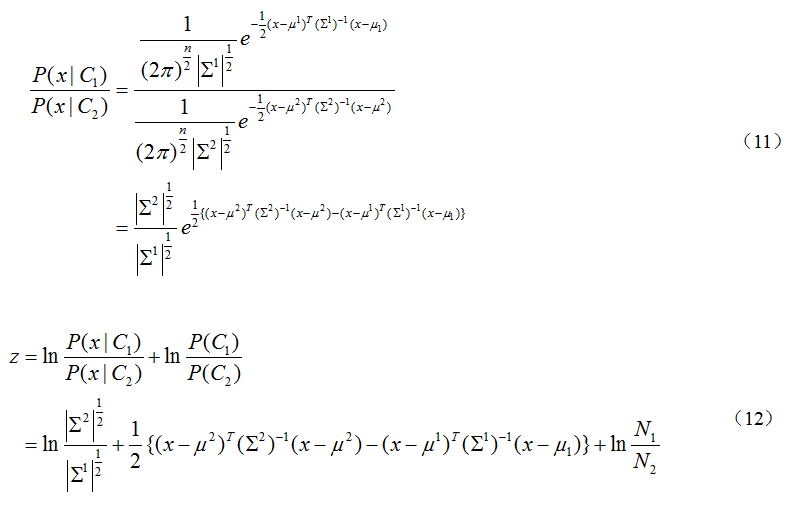
 由于共享参数Σ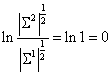，,将（12）的第二项展开，最终的结果有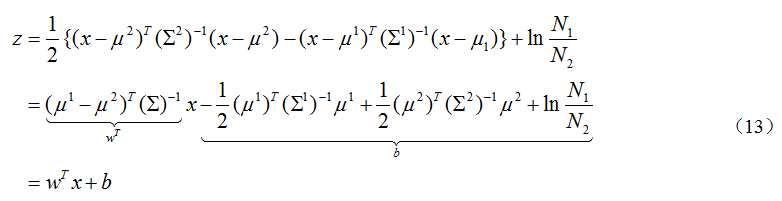 

 将（13）带入（9）有

 

Logistic回归的评估函数

   Logistics回归常用于二分类，如判断一封邮件是否是垃圾邮件；在已知Logistics回归的表达形式（14），如何来确定目标函数，并且最优化目标函数？

以二分类为例，假设数据集如图1-4

图1-4 二分类数据集

则目标函数为（15），我们的目标是找到w,b,使L(w,b)最大化。但通常可以采用最小化某个值来进行参数更新，因此对（15）进行转换

对（15）先取ln，在添加负号有：

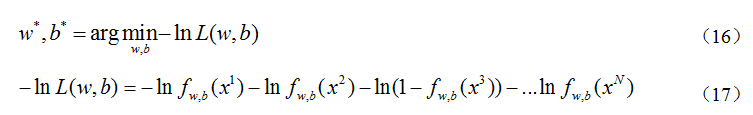
 为了对（17）能有一个统一的描述公式，对数据集的标签进行转换

 

图1-5 二分类标签转换

 

 因此，可以将（17）转换为

 

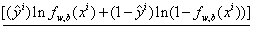 可以看做是两个伯努利分布的cross entropy（交叉熵）

 

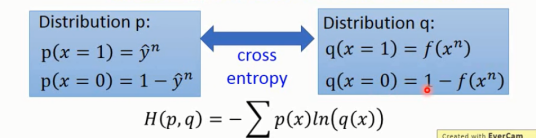
图1-6 cross entropy（交叉熵）示意图 

均方误差作为Logistics回归的缺陷

 将（15）作为目标函数，其假设Logistics生成整个数据集最大概率的参数作为模型的最佳参数。不同于极大似然估计，将极大似然的表达式取负号，采用梯度下降进行整个式子最小化，最终更新参数。

假设使用均方误差作为Logistics的损失函数,损失函数表示如下：

   

 采用梯度下降进行参数更新：

  

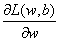  对（20）来说，当表明实际值等于标签值，应停止变化，确实为0；当，表明实际值不等于标签值，参数应发生变化，但也为0，导致参数无法更新；因此，采用均方误差作为Logistics回归的问题在于，有时模型还没达到最优解或者局部最优解，但是参数就已经停止更新。

参考资料

[1]机器学习-李宏毅