数据结构:优先队列
引入优先队列
说明
优先队列是一种抽象数据类型,它是一种排序的机制,它有两个核心操作:找出键值最大(优先级最高)的元素、插入新的元素,效果就是他在维护一个动态的队列。可以收集一些元素,并快速取出键值最大的元素,对其操作后移出队列,然后再收集更多的元素,再处理当前键值最大的元素,如此这般。
例如,我们有一台能够运行多个程序的计算机。计算机通过给每个应用一个优先级属性,将应用根据优先级进行排列,计算机总是处理下一个优先级最高的元素。
泛型优先队列的API
优先队列最重要的操作是删除最大元素和插入元素。

优先队列的初级实现
数组实现(无序)
►思想:
我们维护一个数组,因为不考虑数组顺序,所以我们的插入算法就很简单了。
对于查找最大值,我们利用了选择排序,在找到最大值后,将其与最后一个元素交换,并使长度-1.
► 只给出最简单核心实现步骤:
package queueDemo;
public class QueueANO<T extends Comparable<T>> {
private T[] array;
private int n;
public QueueANO(int capacity)
{
array=(T[]) new Comparable[capacity];
n=0;
}
........
public void insert(T t)
{
array[n]=t;n++;
}
public T delMax()
{
int max=0;
for(int i=1;i<n;i++) //找出最大元素
{
if(less(max,i))
max=i;
}
exch(max,n-1); //将最大元素交换到最后
n--; //长度-1
return array[n];
}
}
数组实现(有序)
►思想:
由于我们维护一个有序数组,所以每次插入元素的时候都要给他找到一个合适位置,来保证数组有序性,删除操作就会很简单了。
►代码:
public class OrderArrayPriorityQueue <Key extends Comparable<Key>>{
private Key[] pq; // elements
private int n; // number of elements
public OrderArrayPriorityQueue(int capacity) {
pq = (Key[]) (new Comparable[capacity]);
n = 0;
}
public boolean isEmpty() { return n == 0; }
public int size() { return n; }
public Key delMax() { return pq[--n]; }
public void insert(Key key) {
int i = n-1;
while (i >= 0 && less(key, pq[i])) {
pq[i+1] = pq[i];
i--;
}
pq[i+1] = key;
n++;
}
private boolean less(Key v, Key w) {
return v.compareTo(w) < 0;
}
public static void main(String[] args) {
OrderArrayPriorityQueue<String> pq = new OrderArrayPriorityQueue<String>(10);
pq.insert("this");
pq.insert("is");
pq.insert("a");
pq.insert("test");
while (!pq.isEmpty())
System.out.println(pq.delMax());
}
}
堆的定义
说明
二叉堆能够很好的实现优先队列的基本操作,二叉堆就是一颗二叉树,但是是按一种特定的组织结构排列。即在二叉堆中每一个节点的值都要保证大于等于另外子节点的值,这也称为大顶堆,即头重脚轻。还有一种排列方式是自上而下依次升高,即每一个节点的值都小于等于其子节点的值,称之为小顶堆。
图示
如下图所示的是一个大顶堆,其根节点一定是所有元素中最大的一个,即优先性最高的,当我们取走后,取代其位置的也应是下一个最大的元素。

说明:
这是一个堆有序的二叉树。所谓堆有序就是一颗二叉树的每个节点都大于等于(或小于)它的两个子节点。
二叉堆表示法
我们可以使用指针来表示,但是这并不是最方便的。通过观察二叉有序堆,我们会发现它是一种完全二叉树,并且完全二叉树可以用数组来表示。用数组实现二叉有序堆,具体方法就是将二叉树的节点按照层序顺序放入数组中,根节点位置在1,它的子节点位置在2,3.依次类推。
两条重要的性质:
1.在一个二叉堆中,位置为K的节点的父节点的位置为|_K/2_|,而它的两个子节点位置为2K和2K+1
2.一颗大小为N的完全二叉树的高度为|_LgN_|
图示堆排序
堆排序实质是对一组关键字进行建堆的过程,这一过程可称为堆的有序化。我们此处将的是大顶堆,小顶堆的道理是相同的。
插入新的元素进行有序化
如下图所示,我们的目标是大顶堆,然而新插入的元素值为9,大于其父元素,所以我们需要进行有序化:
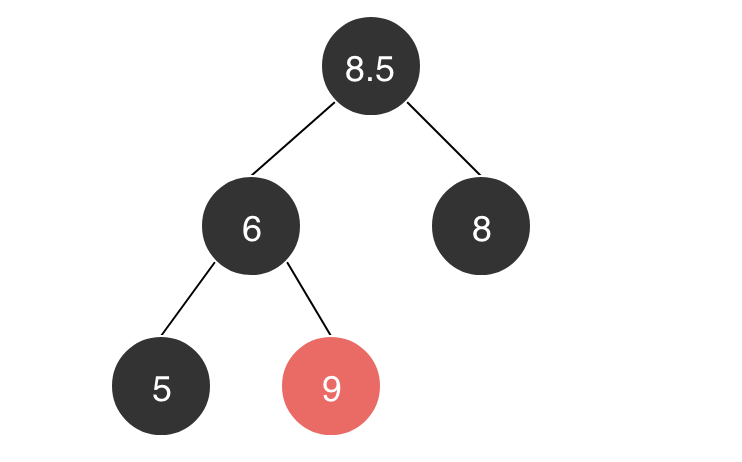
我们将子元素设为X(图中值为9),我们需要交换它和它的父节点(值为6)来修复堆。但是可能交换后X还是很大(大于值为8.5的元素),所以我们需要X一次次的它的祖先节点进行比较,直到找打它最合适的位置。根据二叉堆的性质,我们不难发现只要记住位置为K的节点的父节点为 |_K/2_|,一切都很简单了。
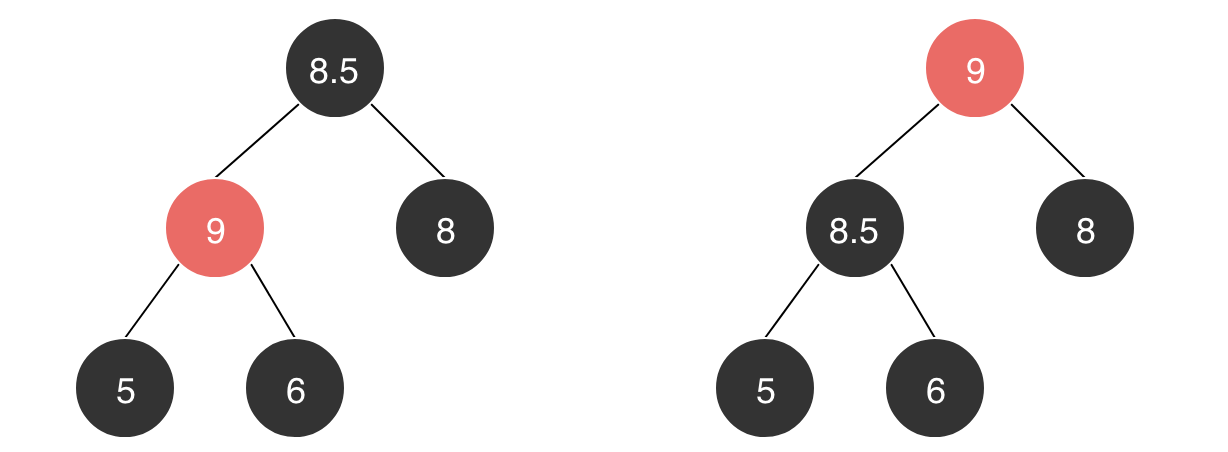
这就是一种上浮操作,即新插入的元素进行上浮,就要需要一次次的它的祖先节点进行比较,直到找打它最合适的位置。
上浮操作核心代码如下:
private void swim(int k) {
while (k > 1 && less(k/2,k)) {
exch(k/2, k);
k = k/2;
}
}
删除堆顶元素后进行有序化
在堆排序中,我们是如何处理删除堆顶元素的呢?我们首先将堆顶元素与序列末端元素进行交换,然后删除末端元素。这是堆顶元素肯定不是堆中最大的元素,所以他需要找到他合适的位置。

为值为6的元素找到其合适位置,它需要和它的子节点中较大的节点进行交换来修复堆,但是可能交换后X还是很小,所以我们需要X一次次的它的子节点进行比较并交换,直到找打它最合适的位置。
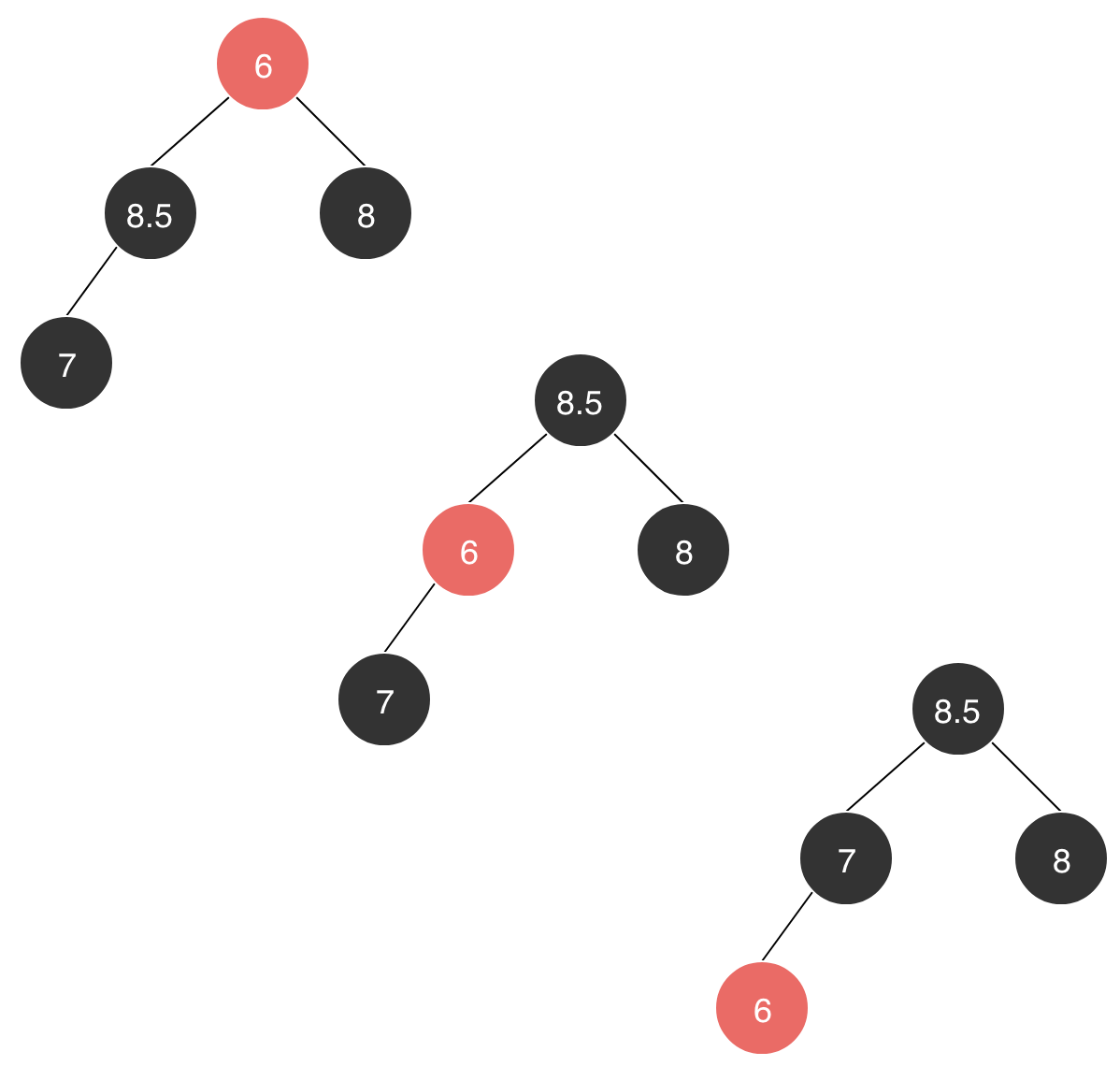
这是一种下沉操作,即被交换后的元素,需要一次次的它的子节点进行比较并交换,直到找打它最合适的位置。
下沉操作核心代码如下:
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1)) {
j++;
}
if (!less(k, j)) {
break;
}
exch(k, j);
k = j;
}
}
到这里位置,我们已经学会了在堆中插入一个新元素和删除堆顶元素的操作,这已然是堆排序的核心内容了。
Java版本实现代码
class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int N = 0;
public MaxPQ(int maxN) {
pq = (Key[]) new Comparable[maxN + 1];
}
public static void main(String[] args) {
MaxPQ<Integer> maxPQ = new MaxPQ<Integer>(10);
for(int i = 0; i < 10; i++)
{
maxPQ.insert((int)(Math.random() * 10 + 1));
}
while(!maxPQ.isEmpty())
{
System.out.println(maxPQ.delMax());
}
}
public int size() {
return N;
}
public boolean isEmpty() {
return N == 0;
}
public void insert(Key v) {
pq[++N] = v;
swim(N);
}
public Key delMax() {
Key max = pq[1];
exch(1,N--);
pq[N + 1] = null;
sink(1);
return max;
}
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1)) {
j++;
}
if (!less(k, j)) {
break;
}
exch(k, j);
k = j;
}
}
private void swim(int k) {
while (k > 1 && less(k/2,k)) {
exch(k/2, k);
k = k/2;
}
}
}