后缀排序
读入一个长度为 n 的由大小写英文字母或数字组成的字符串,请把这个字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 1 到 n 。(n<=10^6)。
https://blog.csdn.net/Bule_Zst/article/details/78604864
首先,倍增法后缀排序,就相当于进行logn次对两位数的基数排序。至于为什么要在每一层中基数排序,这是因为要把每一层后缀的名次求出来,这样才能保证以后基数排序时,桶的大小不超过n。
重要的是如何实现:
const int maxn=1e6+5;
char s[maxn];
int n, m=maxn, r[maxn], sa[maxn];
int *x, *y, *t, wa[maxn], wb[maxn], ws[maxn], wv[maxn], ht[maxn];
int cmp(int *r, int a, int b, int l){
return r[a]==r[b]&&r[a+l]==r[b+l]; }
void Ssort(int *r){
x=wa; y=wb; m=maxn;
int i, j, p=0;
for (i=0; i<m; ++i) ws[i]=0;
for (i=0; i<n; ++i) ++ws[x[i]=r[i]];
for (i=1; i<m; ++i) ws[i]+=ws[i-1];
for (i=0; i<n; ++i) sa[--ws[r[i]]]=i; //sa数组必须排好序
for (j=1; j<n&&p<n; j<<=1, m=p+1){ //p代表当前倍增情况下有多少不同的后缀 m应当变成p+1
for (p=0, i=n-j; i<n; ++i) y[p++]=i;
for (i=0; i<n; ++i) if (sa[i]>=j) y[p++]=sa[i]-j;
for (i=0; i<n; ++i) wv[i]=x[y[i]]; //wv:第二关键词中排i的数,在第一关键词中排第几
for (i=0; i<m; ++i) ws[i]=0;
for (i=0; i<n; ++i) ++ws[x[i]]; //ws:第一关键词中排名为i的数,总排名的范围是多少
for (i=1; i<m; ++i) ws[i]+=ws[i-1];
for (i=n-1; i>=0; --i) sa[--ws[wv[i]]]=y[i];
t=x; x=y; y=t; x[sa[0]]=1; //x要开始接受新的排名了
for (p=1, i=1; i<n; ++i) //rank必须从1开始以区分空串
x[sa[i]]=cmp(y, sa[i-1], sa[i], j)?p:++p; //这句话看上去很可怕,其实只是判断当前后缀和前一个后缀是否相同而已
}
for (i=0; i<n; ++i) --x[i]; p=0;
for (i=0; i<n; ht[x[i++]]=p){ //枚举原串中1到n的所有后缀
if (!x[i]){ p=0; continue; }
for (p?p--:0, j=sa[x[i]-1]; r[i+p]==r[j+p]&&i+p<n; ++p); //p表示h[i]
} return;
}
sa数组的含义是:在第一关键词中,排第几的是谁?(也就是后缀数组)
x数组的含义是:在第一关键词中,你是第几?(也就是名次数组)
y数组的含义是:在第二关键词中,排第几的是谁?
倍增模块外ws[i]的含义:i这个数的最大排名。
倍增模块内ws[i]的含义:第一关键词中排名为i的数,在总排名中的最大排名。
wv[i]的含义:在第二关键词中排第i的数,在第一关键词中排第几?
ws[wv[i]]的含义:在第二关键词中排第i的数,在总排名中的最大排名。
由于(sa[i])表示排第i位的是哪个后缀,因此即使有两个后缀相同,它们的排名也不能相同,不然无法在sa数组中表示。
来看看代码。进入倍增之前,先把原始的sa数组和名次数组求出来。进入倍增后,先求出对于第二关键词的后缀数组y,然后利用y数组求出数组wv:第二关键词中排第i的数,在第一关键词中排第几。接着利用ws[wv[i]]就可以在后缀按第一关键词已经排好序的前提下,将后缀按第二关键词的顺序填充到桶里。
要记住,后缀排序算法中,利用了wv和ws两个中转数组。把它们两个的含义记下来,就会好理解很多。
但是,uoj的板子里面还有一个要求:
除此之外为了进一步证明你确实有给后缀排序的超能力,请另外输出 n−1 个整数分别表示排序后相邻后缀的最长公共前缀的长度。
排在第i位的后缀与第i-1位的后缀的最长公共前缀(LCP)定义为(height[i])。定义(h[i]=height[x[i]]),直观上理解,就是第i个后缀与排在它前一位的那个后缀的LCP。uoj这里要我们求的是height数组。那我们还要h数组干嘛呢?原因是有这样的性质:(h[i]>=h[i-1]-1)。画个图可以直观的理解:
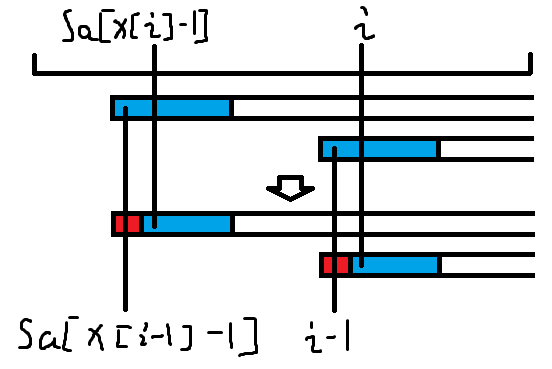
上面两个串的蓝色部分表示(h[i-1]),那么显然,下面的蓝色部分(h[i])是(h[i-1]-1),除非(sa[x[i-1]-1])并不是原来那个(sa[x[i]-1])那个串变成的,而是另外一个字典序比(sa[x[i]-1])大的串,那么此时(h[i]>h[i-1]-1)。因此,我们按照在原串中从小到大的位置处理(height[x[i]])。
- 若(x[i]=1),即这个后缀的字典序是最小的,那么(height[x[i]]=height[1])只能为0。不用比较
- 若(i=1),或者(h[i-1]<=1),那么需要暴力计算(height[x[i]]),由于最多比较(h[i]+1)次,因此比较次数不超过(h[i]-h[i-1]+2)。
- 如果以上两种情况都不满足,那么(S_i)和(S_{i-1})的前驱至少有(h[i-1]-1)个字符相同。因此字符比较只需要从(h[i-1])开始,知道某个字符不相同,计算出(h[i])。比较次数正好为(h[i]-h[i-1]+2)。
因此,总比较次数为(h[n]+2*n),时间复杂度为(O(n))。所以算法的总时间复杂度为(O(nlogn))。
Tip:遇到业界良心(独留)uoj的类似于“aaaaaaaaaaaaaaaa”的测试数据,我猜洛谷上不少人的代码会炸(包括我在之前写的程序)。大家可以去uoj上交一发。
PS:若只需要对字符串两两lcp,则只需要trie。