Atcoder CF 2017 TR I

Atcoder CF 2017 TR I

给定一个有n个点，m条边的图，求为每条边定向，使得从1出发和2出发的两个人可以见面的方案数。

先把问题转换成求all-不能见面的方案数。那么可以把图划分成这样一个集合：

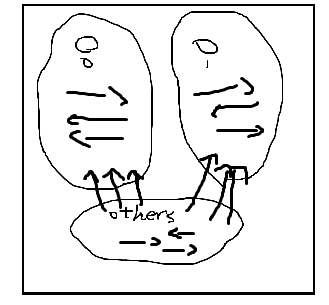
用(f[0/1][i])表示包含0/1的集合i,从0/1出发刚好能到达所有点的方案数 。注意是“刚好“，所以统计的是闭合子图。利用容斥原理求出f，接下来的任务就是统计other集合中，与两个集合不相关的边的个数即可。

#include <cstdio> 
using namespace std;

const int maxn=20, maxm=120, maxs=4e4, p=1e9+7;
int n, m, a[maxm], b[maxm], c[maxs], d[maxs], mi2[maxm];
long long f[2][maxs], ans;  
//f[0/1][i]表示包含0/1的集合i,从0/1出发刚好能到达所有点的方案数 

int main(){
	scanf("%d%d", &n, &m);
	for (int i=mi2[0]=1; i<maxm; ++i)
		mi2[i]=mi2[i-1]*2%p;
	for (int i=0; i<m; ++i){
		scanf("%d%d", &a[i], &b[i]);  //a b 存边 
		--a[i]; --b[i]; }
	for (int i=0; i<(1<<n); ++i)   
		for (int j=0; j<m; ++j){
			if ((i>>a[j]&1)&&(i>>b[j]&1)) ++c[i];  //c:两边都在s中的点数 
			if ((i>>a[j]&1)||(i>>b[j]&1)) ++d[i];  //d:恰好一个点在s中的点数 
		}
	for (int i=0; i<2; ++i)
		for (int j=0; j<1<<n; ++j){
			if ((j>>i&1)==0) continue;
			f[i][j]=mi2[c[j]];
			for (int k=j; k>0; k=(k-1)&j)  //注意是“刚好能到所有点” 
				f[i][j]=(f[i][j]+p-f[i][j-k]*mi2[c[k]])%p;
		}
	for (int i=0; i<1<<n; ++i){
		for (int j=0; j<1<<n; ++j){
			if ((i&j)||c[i]+c[j]!=c[i|j]) continue;
			ans=(ans+f[0][i]*f[1][j]%p*mi2[m-d[i|j]])%p;  //不与集合相连的边随便选 
		}
	}
	printf("%lld
", (mi2[m]-ans+p)%p);
	return 0;
}